北师大版高中数学必修一第三章3.6 指数函数、幂函数、对数函数增长的比较课件(20张)
文档属性
| 名称 | 北师大版高中数学必修一第三章3.6 指数函数、幂函数、对数函数增长的比较课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 13:59:18 | ||
图片预览





文档简介
北师大版高中数学必修一第三章
§3.6 指数函数、幂函数、对数函数增长的比较
情境引入
01
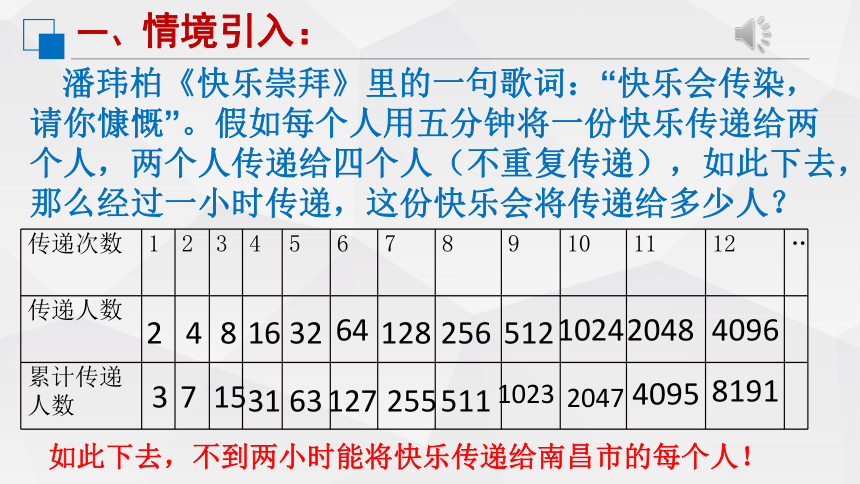
潘玮柏《快乐崇拜》里的一句歌词:“快乐会传染,请你慷慨”。假如每个人用五分钟将一份快乐传递给两个人,两个人传递给四个人(不重复传递),如此下去,那么经过一小时传递,这份快乐会将传递给多少人?
一、情境引入:
如此下去,不到两小时能将快乐传递给南昌市的每个人!
{5940675A-B579-460E-94D1-54222C63F5DA}传递次数
1
2
3
4
5
6
7
8
9
10
11
12
…
传递人数
累计传递人数
2
8
64
4
32
16
256
128
512
1024
2048
4096
3
7
255
511
1023
2047
4095
8191
63
31
127
15
复习旧知
02
二、复习旧知:
问题一:指数函数、幂函数、对数函数中有哪些是增函数?
①指数函数
1.当a>1时,指数函数y=ax是增函数,并且对于x>0,当a越大时,其函数值的增长就越快。
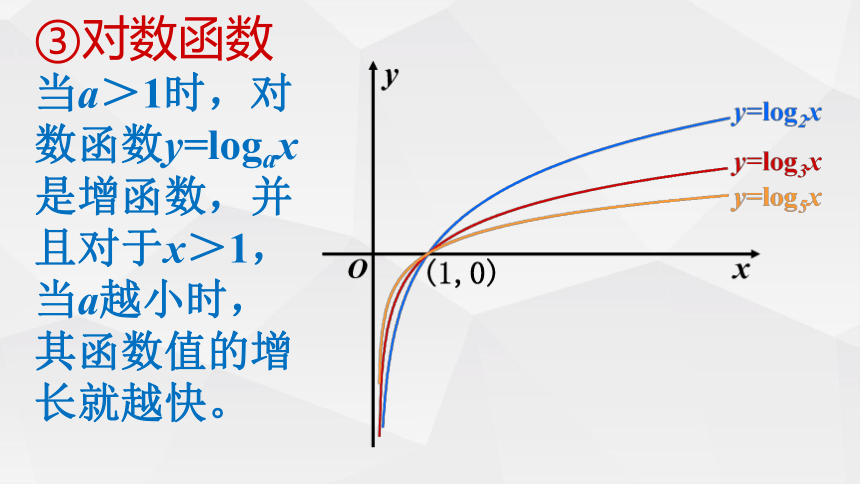
③对数函数
当a>1时,对数函数y=logax是增函数,并且对于x>1,当a越小时,其函数值的增长就越快。
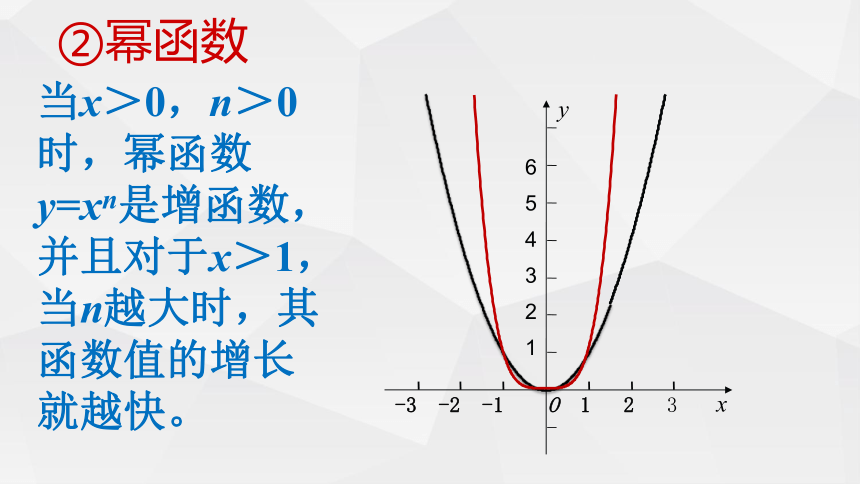
②幂函数
当x>0,n>0时,幂函数y=xn是增函数,并且对于x>1,当n越大时,其函数值的增长就越快。
y
x
-3 -2 -1 O 1 2 3
6
5
4
3
2
1
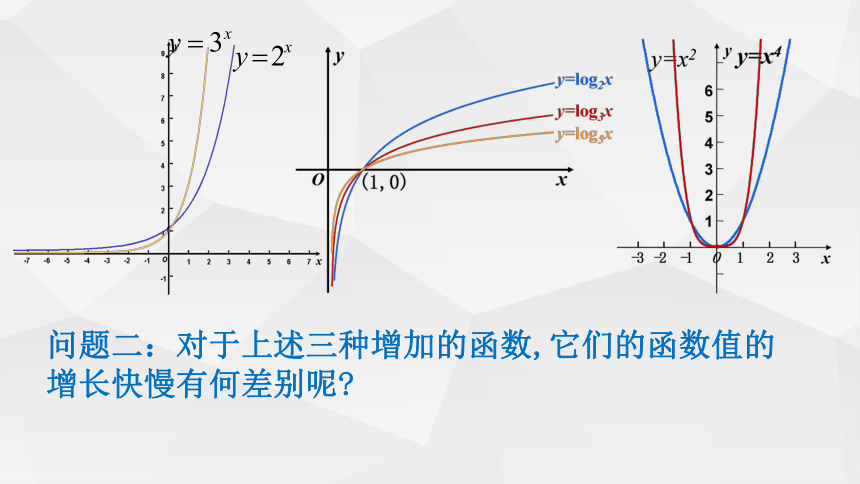
问题二:对于上述三种增加的函数,它们的函数值的增长快慢有何差别呢?
三、探求新知
对函数y=2x,y=x2(x>0),y=log2x的函数值比较
对指数函数 幂函数 和对数函数
的增长性进行比较。
自变量x
函数值
y=2x
y=x2(x>0)
y=log2x
···
···
···
···
1
2
1
0
2
4
4
1
3
8
9
1.584 962
4
16
16
2
5
32
25
2.321 928
···
···
···
···
10
1024
100
3.321 928
11
2048
121
3.459 431
12
4096
144
3.584 962
···
···
···
···
列表对比增长性
图像
例题讲解
03
三、例题讲解:
例
例2、四个变量 随变量x变化的数据如下表
关于x呈指数函数变化的变量是 ( )
例3、你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0 .4元,以后每天的回报比前一天
翻一番.
请问,你会选择哪种投资方案?
令第x天,回报为y元
方案一: y=40方案二: y=10x(x∈N+)方案三: y=2x-1·0.4(x∈N+)
分析:
累计回报
投资1—6天选方案一
投资7天选方案一或方案二
投资8—10天以上选方案二
投资11天及以上选方案三
累计回报
四、课堂小结:
知识:通过三种函数:指数函数,幂函数,对数函数增长性的比较,得到:
在区间(0,+∞)上,当a>1,n>0时,当x足够大时,随着x的增大,y=ax的增长速度越来越快,会超过并远远大于y=xn的增长速度,而y=logax的增长速度则越来越慢.
因此:存在一个x0,
使得当x>x0时,有ax>xn>logax.
思想方法:
转化与化归
数形结合
直观想象
数学建模
数据处理
谢谢
聆听
THANKS
§3.6 指数函数、幂函数、对数函数增长的比较
情境引入
01
潘玮柏《快乐崇拜》里的一句歌词:“快乐会传染,请你慷慨”。假如每个人用五分钟将一份快乐传递给两个人,两个人传递给四个人(不重复传递),如此下去,那么经过一小时传递,这份快乐会将传递给多少人?
一、情境引入:
如此下去,不到两小时能将快乐传递给南昌市的每个人!
{5940675A-B579-460E-94D1-54222C63F5DA}传递次数
1
2
3
4
5
6
7
8
9
10
11
12
…
传递人数
累计传递人数
2
8
64
4
32
16
256
128
512
1024
2048
4096
3
7
255
511
1023
2047
4095
8191
63
31
127
15
复习旧知
02
二、复习旧知:
问题一:指数函数、幂函数、对数函数中有哪些是增函数?
①指数函数
1.当a>1时,指数函数y=ax是增函数,并且对于x>0,当a越大时,其函数值的增长就越快。
③对数函数
当a>1时,对数函数y=logax是增函数,并且对于x>1,当a越小时,其函数值的增长就越快。
②幂函数
当x>0,n>0时,幂函数y=xn是增函数,并且对于x>1,当n越大时,其函数值的增长就越快。
y
x
-3 -2 -1 O 1 2 3
6
5
4
3
2
1
问题二:对于上述三种增加的函数,它们的函数值的增长快慢有何差别呢?
三、探求新知
对函数y=2x,y=x2(x>0),y=log2x的函数值比较
对指数函数 幂函数 和对数函数
的增长性进行比较。
自变量x
函数值
y=2x
y=x2(x>0)
y=log2x
···
···
···
···
1
2
1
0
2
4
4
1
3
8
9
1.584 962
4
16
16
2
5
32
25
2.321 928
···
···
···
···
10
1024
100
3.321 928
11
2048
121
3.459 431
12
4096
144
3.584 962
···
···
···
···
列表对比增长性
图像
例题讲解
03
三、例题讲解:
例
例2、四个变量 随变量x变化的数据如下表
关于x呈指数函数变化的变量是 ( )
例3、你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0 .4元,以后每天的回报比前一天
翻一番.
请问,你会选择哪种投资方案?
令第x天,回报为y元
方案一: y=40方案二: y=10x(x∈N+)方案三: y=2x-1·0.4(x∈N+)
分析:
累计回报
投资1—6天选方案一
投资7天选方案一或方案二
投资8—10天以上选方案二
投资11天及以上选方案三
累计回报
四、课堂小结:
知识:通过三种函数:指数函数,幂函数,对数函数增长性的比较,得到:
在区间(0,+∞)上,当a>1,n>0时,当x足够大时,随着x的增大,y=ax的增长速度越来越快,会超过并远远大于y=xn的增长速度,而y=logax的增长速度则越来越慢.
因此:存在一个x0,
使得当x>x0时,有ax>xn>logax.
思想方法:
转化与化归
数形结合
直观想象
数学建模
数据处理
谢谢
聆听
THANKS
