北师大版高中数学必修一第三章指数函数课件(50张)
文档属性
| 名称 | 北师大版高中数学必修一第三章指数函数课件(50张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览







文档简介
指数函数
回忆
一般地,函数____________ (a>0,a≠1,x∈N+)叫作正整数指数函数,其中 x是自变量,定义域是正整数集N+.
想一想
如果把定义域的范围扩大到R又会有什么新发现
特征:
【提示】依据指数函数y=ax(a>0且a≠1)解析式的结构特征
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:只有一项ax ,系数为1
定义
1.下列以x为自变量的函数中,是指数函数的是( )
2. 函数 是指数函数,则a=_____
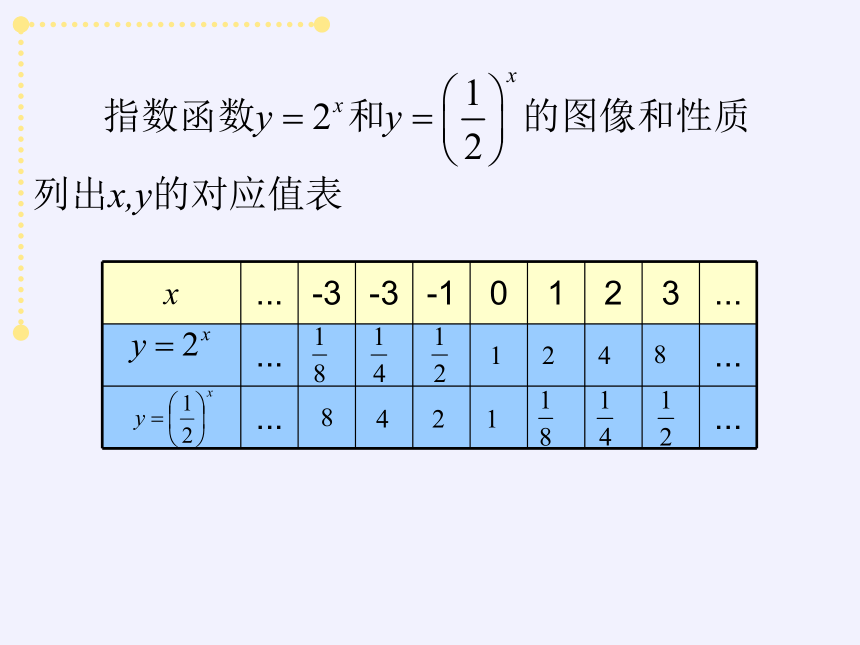
同桌分工合作,分别画出两个指数函数的图像
列表→描点→连线
指数函数y= 和y= 的
图像和性质
x
...
-3
-3
-1
0
1
2
3
...
...
...
...
...
列出x,y的对应值表
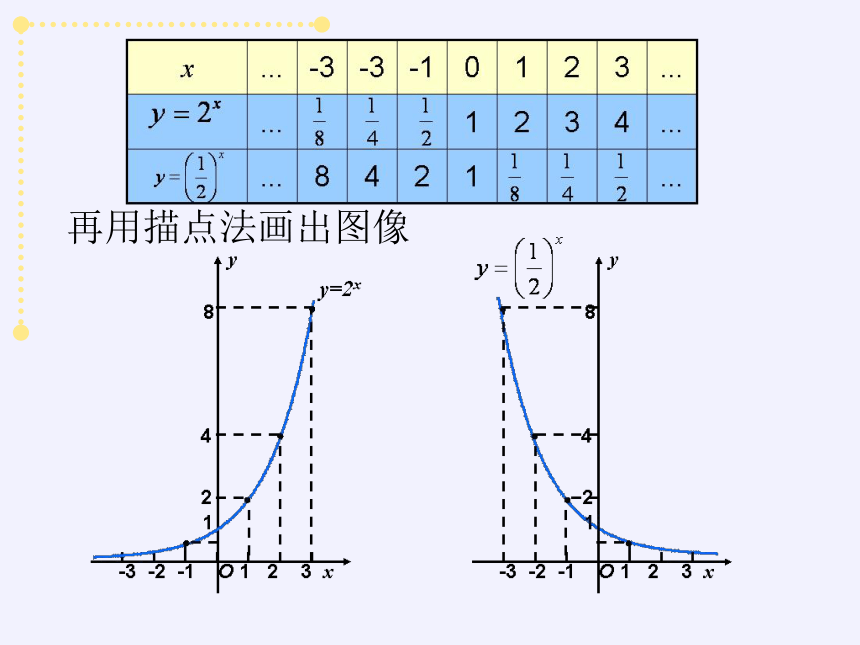
再用描点法画出图像
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
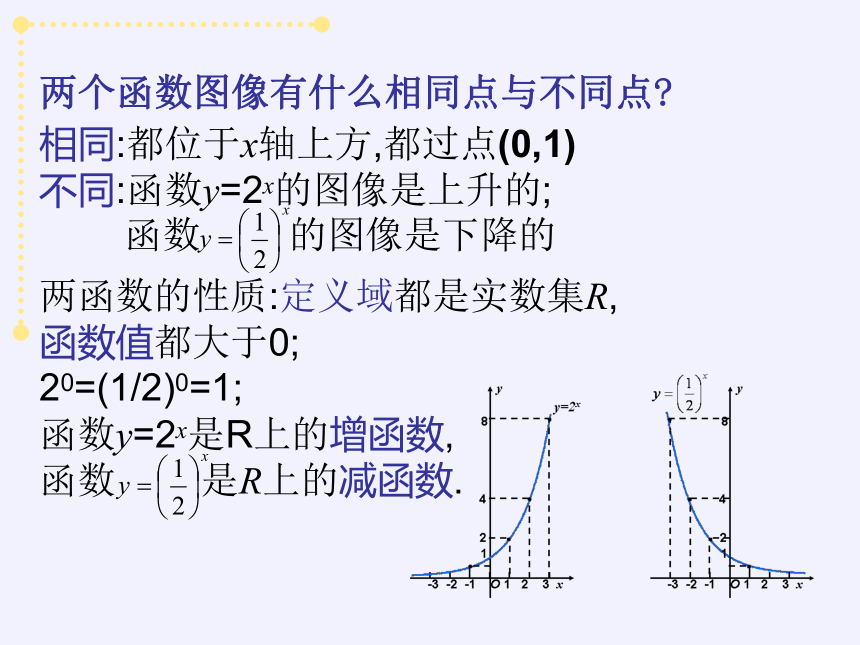
两个函数图像有什么相同点与不同点?
相同:都位于x轴上方,都过点(0,1)
不同:函数y=2x的图像是上升的;
函数 的图像是下降的
两函数的性质:定义域都是实数集R,
函数值都大于0;
20=(1/2)0=1;
函数y=2x是R上的增函数,
函数 是R上的减函数.
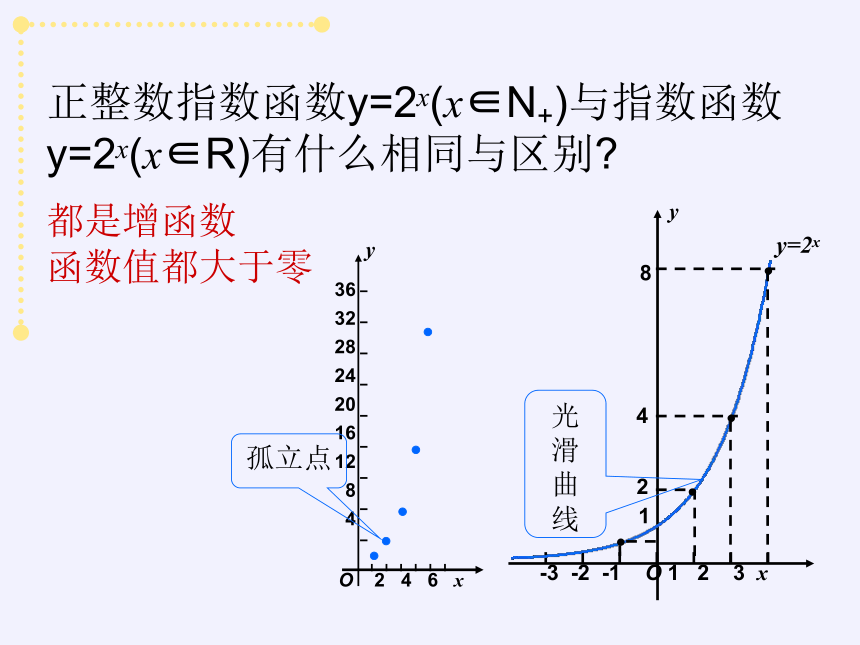
正整数指数函数y=2x(x∈N+)与指数函数
y=2x(x∈R)有什么相同与区别?
36
32
28
24
20
16
12
8
4
O 2 4 6 x
y
-3 -2 -1 O 1 2 3 x
8
4
2
1
y
y=2x
都是增函数
函数值都大于零
孤立点
光滑曲线
3、比较下列数的大小
(1) 20.89________20.95
(2)0.50.74________0.50.91
(3)0.5-8_________0.54
?
?
?
4.下图是指数函数y=2x的图像,试由x的下列各值,确定函数y的值(精确到0.1):
-4, -2, -0.5, 0, 1.5, 3.
0.1 0.2 0.8 1.0 3.0 8.0
5.利用下图,找出适合方程2x=5的近似解(精确到0.1).
2x=5的近似解为2.4.
如何学习一个函数
在同一坐标系中分别作出如下函数的图像:
列表如下:
x
…
-2.5
-2
-1
-0.5
0
0.5
1
2
2.5
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
15.6
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
0.06
…
x
…
-2.5
-2
-1
-0.5
0
0.5
1
2
2.5
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
15.6
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
0.06
…
( )
通过作图,我们发现y=ax的图象大致分两种类型,即0<a<1和a>1,图象如下:
x
y
(0,1)
y = 1
y = a x
(a> 1)
0
x
y
y = 1
y =a x
(0<a <1)
(0,1)
0
指数函数 在底数 及 这两种情况下的图象和性质
a>1
0<a<1
图 象
性 质
0
x
y
(0,1)
y=1
y
x
(0,1)
y=1
o
(1)定义域: R
(2)值域 : (0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)在R上是增函数
(4)在R上是减函数
想一想
2、函数y=15x的图像是( )
解析:选B.x=0,y=1,且为增函数.
答案:D
4、已知函数y=ax+b的图像经过第一、三、四象限,试确定a,b的取值范围.
[分析]函数y=ax+b的图像是由y=ax的图像向上(b>0)或向下(b<0)平移|b|个单位得到的,其形状与y=ax的图像相同.
[解析] 如图所示,当x=0时,y<0,
∴a0+b<0,∴b<-1,显然a>1.
故a∈(1,+∞),b∈(-∞,-1).
[点评] 利用熟悉的函数图像作图,再利用图像的平移、对称等变换,平移需分清向哪个方向移,再移多少个单位.
5、说明下列函数的图象与指数函数 的图象的关系,并画出它们的示意图:
(1)
(2)
解:(1)比较函数 与 的关系:
与 相等,
与 相等,
与 相等,
由此可以知道,将指数函数 的图象向左平移1个单位长度,就得到函数 的图象。
说明:一般地,当时a>0时,将函数y=f(x)的图象向左平移a个单位得到y=f(x+a)的图象;
当时a<0时,将函数y=f(x)的图象向右平移|a|个单位得到的y=f(x+a)图象;
1、比较下列各题中两个值的大小:
(1) 1.72.5, 1.73;
(2) 0.8-0.1, 0.8-0.2;
(3) 1.70.3, 0.93.1.
对上述解题过程,可总结出比较同底数幂大小的方法,即用指数函数的单调性,其基本步骤如下:
(1)确定所要考查的指数函数;
(2)根据底数情况指出已确定的指数函数的单调性;
(3)比较指数大小,然后利用指数函数单调性得出同底数幂的大小关系。
(4)对于不同底不同指数的函数值比较大小,一般要找中间量或特殊值。
利用指数函数单调性比较大小
新知应用
④
解:④ 作商比较即可
所以
2.比较下列各题中两数值的大小
① 1.62.4,1.63. ② 0.9-0.1 ,0.9-0.2③
解:① 指数函数y=1.6x 在R上是增函数. 2.4<3 , ∴ 1.62.4<1.63
③因为指数函数y= 是R上增函数.y= 是R上减函数
∴
∴
②指数函数y= 0.9x在R上是减函数.
-0.1>-0.2 ∴0.9-0.1 < 0.9-0.2
课堂练习
① 0.79-0.1 0.790.1
② 2.012.8 2.013.5
③ b2 b4(0④ a0.3与a0.4 (a>0 且a≠1)
<
>
>
3.比较下列数的大小
4、已知下列不等式,比较m、n的大小。
① 2m<2n ②0.2m>0.2n
③ am>an (a≠1且a>1)
解:① m③当a>1时,m>n,当0 指数式的比较大小有3种形式
(1)底数相同,指数不同(利用指数函数的单调性判断大小)
(2)底数不同,指数相同(利用函数图像或作商判断大小)
(3)底数不同,指数也不同(利用函数图像或特殊值比较大小)
5.若2x+1<1,则x的取值范围是( )
A.(-1,1)
B.(-1,+∞)
C.(0,1)∪(1,+∞)
D.(-∞,-1)
[答案] D
[解析] ∵2x+1<1=20,且y=2x是增函数,
∴x+1<0,∴x<-1.
1.指数函数 的图象经过点 , 求 的值
指数函数性质的综合应用
变式训练
[规律总结] 对于形如y=af(x)(a>0且a≠1)一类的函数,有以下结论:
(1)函数y=af(x)的定义域、奇偶性与f(x)的定义域、奇偶性相同;
(2)先确定函数f(x)的值域,再根据指数函数的单调性,求函数y=af(x)的值域;
(3)当a>1时,函数y=af(x)与函数f(x)在相应区间上的单调性相同;当0?
?
1.如图所示是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图像,则a,b,c,d与1的大小关系是( )
A.a C.1[思路分析] 作直线x=1,其与函数的交点纵坐标即为底数的值.
[规范解答] 解法1:在①②中底数小于1且大于零,在y轴右边,底数越小,图像向下越靠近x轴,故有b解法2:作直线x=1,与四个图像分别交于A、B、C、D四点,由于x=1代入各个函数可得函数值等于底数的大小,所以若四个交点的纵坐标越大,则底数越大,由图可知b[答案] B
结论:
?
课堂小结
指数函数 的图象和性质
a>1
0<a<1
图 象
性 质
0
x
y
(0,1)
y=1
y
x
(0,1)
y=1
o
(1)定义域: R
(2)值域 : (0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)在R上是增函数
(4)在R上是减函数
指数式的比较大小有3种形式
(1)底数相同,指数不同(利用指数函数的单调性判断大小)
(2)底数不同,指数相同(利用函数图像或作商判断大小)
(3)底数不同,指数也不同(利用函数图像或特殊值比较大小)
回忆
一般地,函数____________ (a>0,a≠1,x∈N+)叫作正整数指数函数,其中 x是自变量,定义域是正整数集N+.
想一想
如果把定义域的范围扩大到R又会有什么新发现
特征:
【提示】依据指数函数y=ax(a>0且a≠1)解析式的结构特征
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:只有一项ax ,系数为1
定义
1.下列以x为自变量的函数中,是指数函数的是( )
2. 函数 是指数函数,则a=_____
同桌分工合作,分别画出两个指数函数的图像
列表→描点→连线
指数函数y= 和y= 的
图像和性质
x
...
-3
-3
-1
0
1
2
3
...
...
...
...
...
列出x,y的对应值表
再用描点法画出图像
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
两个函数图像有什么相同点与不同点?
相同:都位于x轴上方,都过点(0,1)
不同:函数y=2x的图像是上升的;
函数 的图像是下降的
两函数的性质:定义域都是实数集R,
函数值都大于0;
20=(1/2)0=1;
函数y=2x是R上的增函数,
函数 是R上的减函数.
正整数指数函数y=2x(x∈N+)与指数函数
y=2x(x∈R)有什么相同与区别?
36
32
28
24
20
16
12
8
4
O 2 4 6 x
y
-3 -2 -1 O 1 2 3 x
8
4
2
1
y
y=2x
都是增函数
函数值都大于零
孤立点
光滑曲线
3、比较下列数的大小
(1) 20.89________20.95
(2)0.50.74________0.50.91
(3)0.5-8_________0.54
?
?
?
4.下图是指数函数y=2x的图像,试由x的下列各值,确定函数y的值(精确到0.1):
-4, -2, -0.5, 0, 1.5, 3.
0.1 0.2 0.8 1.0 3.0 8.0
5.利用下图,找出适合方程2x=5的近似解(精确到0.1).
2x=5的近似解为2.4.
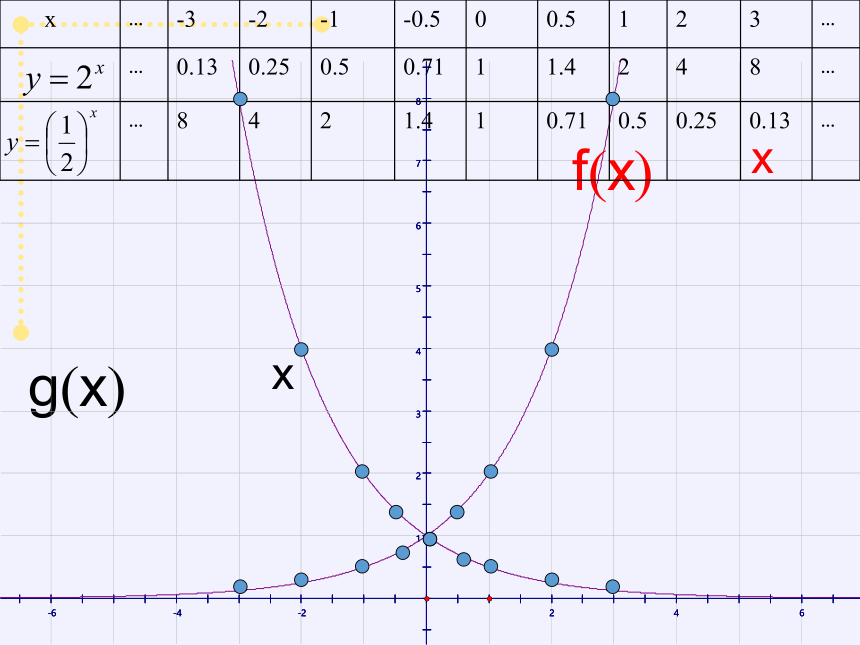
如何学习一个函数
在同一坐标系中分别作出如下函数的图像:
列表如下:
x
…
-2.5
-2
-1
-0.5
0
0.5
1
2
2.5
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
15.6
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
0.06
…
x
…
-2.5
-2
-1
-0.5
0
0.5
1
2
2.5
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
15.6
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
0.06
…
( )
通过作图,我们发现y=ax的图象大致分两种类型,即0<a<1和a>1,图象如下:
x
y
(0,1)
y = 1
y = a x
(a> 1)
0
x
y
y = 1
y =a x
(0<a <1)
(0,1)
0
指数函数 在底数 及 这两种情况下的图象和性质
a>1
0<a<1
图 象
性 质
0
x
y
(0,1)
y=1
y
x
(0,1)
y=1
o
(1)定义域: R
(2)值域 : (0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)在R上是增函数
(4)在R上是减函数
想一想
2、函数y=15x的图像是( )
解析:选B.x=0,y=1,且为增函数.
答案:D
4、已知函数y=ax+b的图像经过第一、三、四象限,试确定a,b的取值范围.
[分析]函数y=ax+b的图像是由y=ax的图像向上(b>0)或向下(b<0)平移|b|个单位得到的,其形状与y=ax的图像相同.
[解析] 如图所示,当x=0时,y<0,
∴a0+b<0,∴b<-1,显然a>1.
故a∈(1,+∞),b∈(-∞,-1).
[点评] 利用熟悉的函数图像作图,再利用图像的平移、对称等变换,平移需分清向哪个方向移,再移多少个单位.
5、说明下列函数的图象与指数函数 的图象的关系,并画出它们的示意图:
(1)
(2)
解:(1)比较函数 与 的关系:
与 相等,
与 相等,
与 相等,
由此可以知道,将指数函数 的图象向左平移1个单位长度,就得到函数 的图象。
说明:一般地,当时a>0时,将函数y=f(x)的图象向左平移a个单位得到y=f(x+a)的图象;
当时a<0时,将函数y=f(x)的图象向右平移|a|个单位得到的y=f(x+a)图象;
1、比较下列各题中两个值的大小:
(1) 1.72.5, 1.73;
(2) 0.8-0.1, 0.8-0.2;
(3) 1.70.3, 0.93.1.
对上述解题过程,可总结出比较同底数幂大小的方法,即用指数函数的单调性,其基本步骤如下:
(1)确定所要考查的指数函数;
(2)根据底数情况指出已确定的指数函数的单调性;
(3)比较指数大小,然后利用指数函数单调性得出同底数幂的大小关系。
(4)对于不同底不同指数的函数值比较大小,一般要找中间量或特殊值。
利用指数函数单调性比较大小
新知应用
④
解:④ 作商比较即可
所以
2.比较下列各题中两数值的大小
① 1.62.4,1.63. ② 0.9-0.1 ,0.9-0.2③
解:① 指数函数y=1.6x 在R上是增函数. 2.4<3 , ∴ 1.62.4<1.63
③因为指数函数y= 是R上增函数.y= 是R上减函数
∴
∴
②指数函数y= 0.9x在R上是减函数.
-0.1>-0.2 ∴0.9-0.1 < 0.9-0.2
课堂练习
① 0.79-0.1 0.790.1
② 2.012.8 2.013.5
③ b2 b4(0
<
>
>
3.比较下列数的大小
4、已知下列不等式,比较m、n的大小。
① 2m<2n ②0.2m>0.2n
③ am>an (a≠1且a>1)
解:① m
(1)底数相同,指数不同(利用指数函数的单调性判断大小)
(2)底数不同,指数相同(利用函数图像或作商判断大小)
(3)底数不同,指数也不同(利用函数图像或特殊值比较大小)
5.若2x+1<1,则x的取值范围是( )
A.(-1,1)
B.(-1,+∞)
C.(0,1)∪(1,+∞)
D.(-∞,-1)
[答案] D
[解析] ∵2x+1<1=20,且y=2x是增函数,
∴x+1<0,∴x<-1.
1.指数函数 的图象经过点 , 求 的值
指数函数性质的综合应用
变式训练
[规律总结] 对于形如y=af(x)(a>0且a≠1)一类的函数,有以下结论:
(1)函数y=af(x)的定义域、奇偶性与f(x)的定义域、奇偶性相同;
(2)先确定函数f(x)的值域,再根据指数函数的单调性,求函数y=af(x)的值域;
(3)当a>1时,函数y=af(x)与函数f(x)在相应区间上的单调性相同;当0
?
1.如图所示是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图像,则a,b,c,d与1的大小关系是( )
A.a
[规范解答] 解法1:在①②中底数小于1且大于零,在y轴右边,底数越小,图像向下越靠近x轴,故有b
结论:
?
课堂小结
指数函数 的图象和性质
a>1
0<a<1
图 象
性 质
0
x
y
(0,1)
y=1
y
x
(0,1)
y=1
o
(1)定义域: R
(2)值域 : (0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)在R上是增函数
(4)在R上是减函数
指数式的比较大小有3种形式
(1)底数相同,指数不同(利用指数函数的单调性判断大小)
(2)底数不同,指数相同(利用函数图像或作商判断大小)
(3)底数不同,指数也不同(利用函数图像或特殊值比较大小)
