高中数学人教A版必修1第二章-2.2.1对数与对数运算课件(21张)
文档属性
| 名称 | 高中数学人教A版必修1第二章-2.2.1对数与对数运算课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 614.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览








文档简介
2.2.1对数与对数运算
(第一课时)
创设情境、导入新课
3+2=5
如何用另外两个数字来表示3或2呢?3=5__2,2=5__3
这说明加法的逆运算是
减法
类似的乘法的逆运算是
除法
-
-
用3和8怎样表示2=?
创设情境、导入新课
根据立方根概念
2=
为了解决这类问题,我们引入一个新的概念
对数
3=?
乘方(指数)式中,已知底数和幂,求指数时,无法通过开方运算来实现
创设情境、导入新课
创设情境、导入新课
18世纪瑞士数学家欧拉指出:对数源于指数。
对数的发明者是苏格兰数学家纳皮尔(J.Napier)(1614年出版《奇妙的对数》)
更奇妙的是:他是在指数的书写方法发明之前完成的。
下面我们就从指数入手
引导探究,获得新知
例如:在 =8中
我们称3是以2为底8的对数
练习(1) (2)
幂指数 又叫做以 为底 的对数。
怎样书写?
我们常用“log”(拉丁文logarithm的缩写)表示对数。那么,3是以2为底8的对数,就可以写成:
引导探究,获得新知
推广
0是以2为底1的对数,就可以写成:
对数的概念:一般地,对于指数式
我们把“以 为底 的对数 ”记
即
其中,数 叫做 叫做 ,读作.
引导探究,获得新知
对数的底数
真数
“ 等于以 为底 的对数”
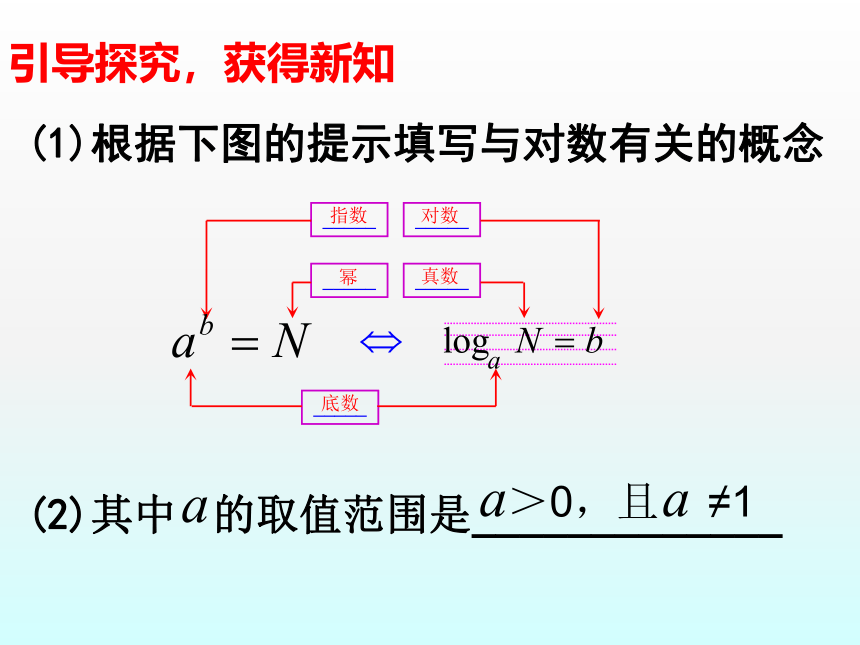
(1)根据下图的提示填写与对数有关的概念
(2)其中 的取值范围是_____________
_____
_____
_____
_____
_____
指数
对数
真数
幂
底数
引导探究,获得新知
>0,且 ≠1
例1.将下列指数式改写成对数式
(1) (2) (3)
例2.将下列对数式改写成指数式
(1) (2) (3)
总结提升:指对互化,形式等价
知识应用,巩固理解
思考: 二者组合可得什么?
知识应用,巩固理解
练习1.求 与 的值:
知识应用,巩固理解
这说明乘方(指数)的逆运算有
两种:
开方和对数
有何启发?
探究活动一:
对于对数
(1)当N为负数时 (2)当N为0时
思考1:您发现了什么?
探究活动二:
求下列各式的值:(1) (2)
思考2:您发现了什么?
引导探究,获得新知
探究活动三:
求下列各式的值:(1) (2)
思考3:您发现了什么?
① 0和负数没有对数,即
② 1的对数为0,
③ 底的对数等于1,
归纳对数的性质:
引导探究,获得新知
纳皮尔的朋友—布立格(数学家,天文学家)
他通过研究《奇妙的对数》,感到其中的对数用起来很不方便(我们的数系是十进制),不顾路途遥远从伦敦到苏格兰拜会纳皮尔求教,他们互相帮助,亲密合作,到1624年,布里格出版了《对数》公布了10为底包含1至20000及90000至100000的14位常用对数表。人民为了纪念他,也把以10为底的对数叫做“布立格对数”。
如果说我比别人看得更远些,那是因为我站在了巨人的肩上.
定义:常用对数又称“十进对数”(以10为底,符号是lg)出现了以10为底的对数叫做常用对数,把 记做
口算: .
例3.求下列对数的值。
3
-3
知识应用,能力提升
2
知识应用,能力提升
练习2.求下列各式x的值
知识应用,能力提升
例4.已知 ,
则实数 =____.
课堂小结、布置作业
通过本节课,有什么收获?
从特殊到一般的学习方法
对数的定义和本质
对数的性质
类比的学习方法
伟大的导师恩格斯在他的著作《自然辩证法》中,曾经把笛卡尔的坐标、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为十七世纪的三大数学发明。(地位)
伽利略也说过:“给我空间、时间、和对数,我就可以创造一个宇宙。(价值)
(第一课时)
创设情境、导入新课
3+2=5
如何用另外两个数字来表示3或2呢?3=5__2,2=5__3
这说明加法的逆运算是
减法
类似的乘法的逆运算是
除法
-
-
用3和8怎样表示2=?
创设情境、导入新课
根据立方根概念
2=
为了解决这类问题,我们引入一个新的概念
对数
3=?
乘方(指数)式中,已知底数和幂,求指数时,无法通过开方运算来实现
创设情境、导入新课
创设情境、导入新课
18世纪瑞士数学家欧拉指出:对数源于指数。
对数的发明者是苏格兰数学家纳皮尔(J.Napier)(1614年出版《奇妙的对数》)
更奇妙的是:他是在指数的书写方法发明之前完成的。
下面我们就从指数入手
引导探究,获得新知
例如:在 =8中
我们称3是以2为底8的对数
练习(1) (2)
幂指数 又叫做以 为底 的对数。
怎样书写?
我们常用“log”(拉丁文logarithm的缩写)表示对数。那么,3是以2为底8的对数,就可以写成:
引导探究,获得新知
推广
0是以2为底1的对数,就可以写成:
对数的概念:一般地,对于指数式
我们把“以 为底 的对数 ”记
即
其中,数 叫做 叫做 ,读作.
引导探究,获得新知
对数的底数
真数
“ 等于以 为底 的对数”
(1)根据下图的提示填写与对数有关的概念
(2)其中 的取值范围是_____________
_____
_____
_____
_____
_____
指数
对数
真数
幂
底数
引导探究,获得新知
>0,且 ≠1
例1.将下列指数式改写成对数式
(1) (2) (3)
例2.将下列对数式改写成指数式
(1) (2) (3)
总结提升:指对互化,形式等价
知识应用,巩固理解
思考: 二者组合可得什么?
知识应用,巩固理解
练习1.求 与 的值:
知识应用,巩固理解
这说明乘方(指数)的逆运算有
两种:
开方和对数
有何启发?
探究活动一:
对于对数
(1)当N为负数时 (2)当N为0时
思考1:您发现了什么?
探究活动二:
求下列各式的值:(1) (2)
思考2:您发现了什么?
引导探究,获得新知
探究活动三:
求下列各式的值:(1) (2)
思考3:您发现了什么?
① 0和负数没有对数,即
② 1的对数为0,
③ 底的对数等于1,
归纳对数的性质:
引导探究,获得新知
纳皮尔的朋友—布立格(数学家,天文学家)
他通过研究《奇妙的对数》,感到其中的对数用起来很不方便(我们的数系是十进制),不顾路途遥远从伦敦到苏格兰拜会纳皮尔求教,他们互相帮助,亲密合作,到1624年,布里格出版了《对数》公布了10为底包含1至20000及90000至100000的14位常用对数表。人民为了纪念他,也把以10为底的对数叫做“布立格对数”。
如果说我比别人看得更远些,那是因为我站在了巨人的肩上.
定义:常用对数又称“十进对数”(以10为底,符号是lg)出现了以10为底的对数叫做常用对数,把 记做
口算: .
例3.求下列对数的值。
3
-3
知识应用,能力提升
2
知识应用,能力提升
练习2.求下列各式x的值
知识应用,能力提升
例4.已知 ,
则实数 =____.
课堂小结、布置作业
通过本节课,有什么收获?
从特殊到一般的学习方法
对数的定义和本质
对数的性质
类比的学习方法
伟大的导师恩格斯在他的著作《自然辩证法》中,曾经把笛卡尔的坐标、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为十七世纪的三大数学发明。(地位)
伽利略也说过:“给我空间、时间、和对数,我就可以创造一个宇宙。(价值)
