高中数学人教A版必修1第二章-2.2.2 对数函数及其性质课件(38张)
文档属性
| 名称 | 高中数学人教A版必修1第二章-2.2.2 对数函数及其性质课件(38张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 953.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 15:24:14 | ||
图片预览









文档简介
2.2.2 对数函数及其性质 (一)
预习中存在的问题
1.画图不规范
2.对对数函数的定义式理解不够到位
3.求函数的定义域存在问题
学习目标
1.理解对数函数的定义;
2.熟悉对数函数的图象与性质.
我们研究指数函数时,曾讨论过折纸问题,折纸一次,变成两面,折两次,纸变成4面,…,设折x次后,得到纸的面数为y,则
那么,如果知道纸的面数y,如何得到折纸次数x?
y=2x,x∈N*
观察,这个式子有什么特点?
(1)底数为大于0且不等于1的常数,不含有自变量x;
(2) 自变量x在真数位置,且x的系数是1;
(3)log2x的系数是1.
一般地,我们把函数 叫
做对数函数,其中x是自变量,函数的定义域是
探究1:对数函数的定义
y=logax(a>0,且a≠1)
(0,+∞).
1.下列函数是对数函数的是_______.
A
2.对数函数f(x)的图象过点(4,2),求f(x), f(8)
变式训练
解:设对数函数解析式为
因为函数图象过点(4,2)所以 即
得a=2,对数函数解析式为
先画出函数的图象,再借助图象研究其性质
回想一下,我们是如何研究指数函数的?
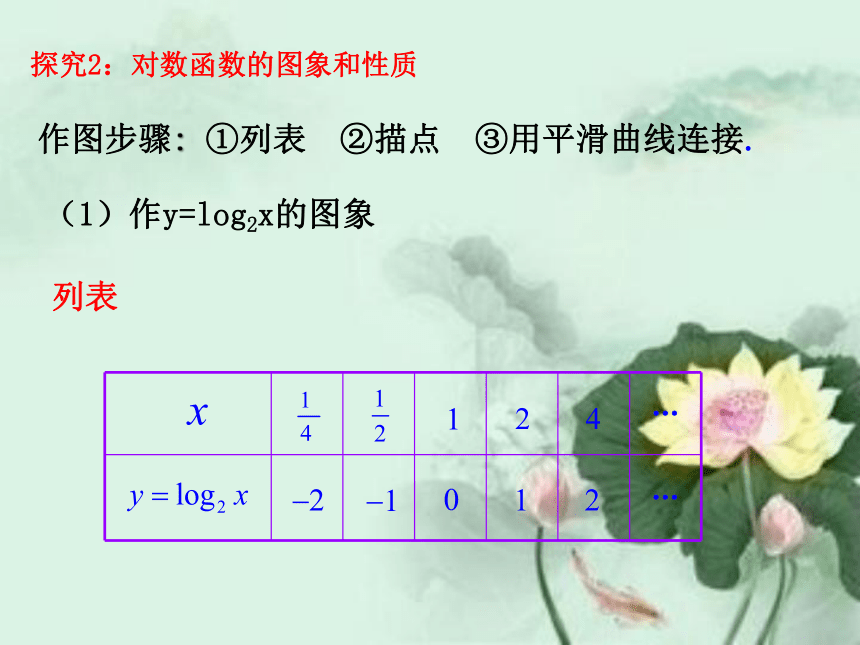
探究2:对数函数的图象和性质
(1)作y=log2x的图象
…
…
列表
作图步骤: ①列表 ②描点 ③用平滑曲线连接.
描点
连线
2
1
-1
-2
2
4
O
y
x
3
1
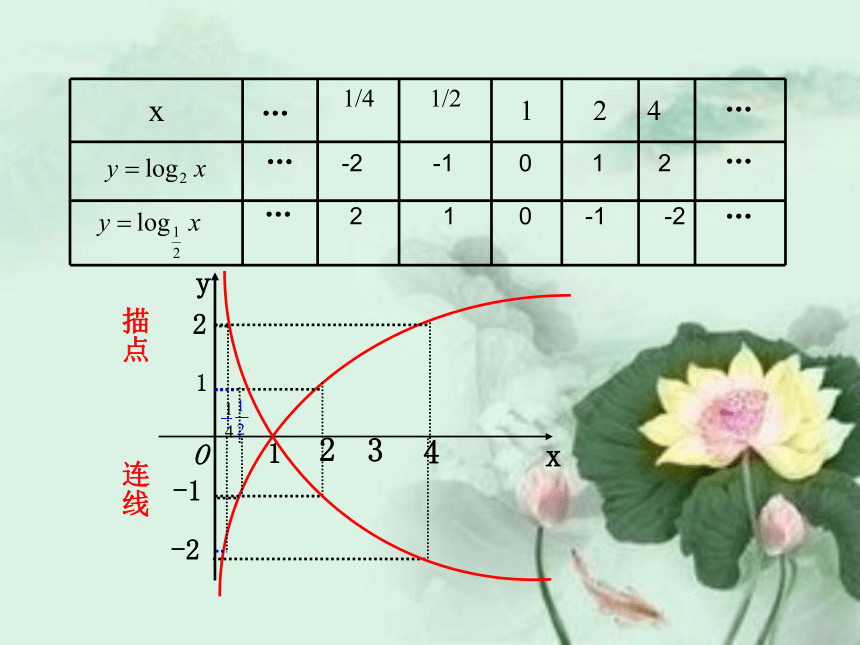
同样的方法在同坐标系中作出函数 的图象,并指出二者的关系
描点
连线
2
1
-1
-2
1
2
4
O
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
…
…
…
…
…
…
1
4
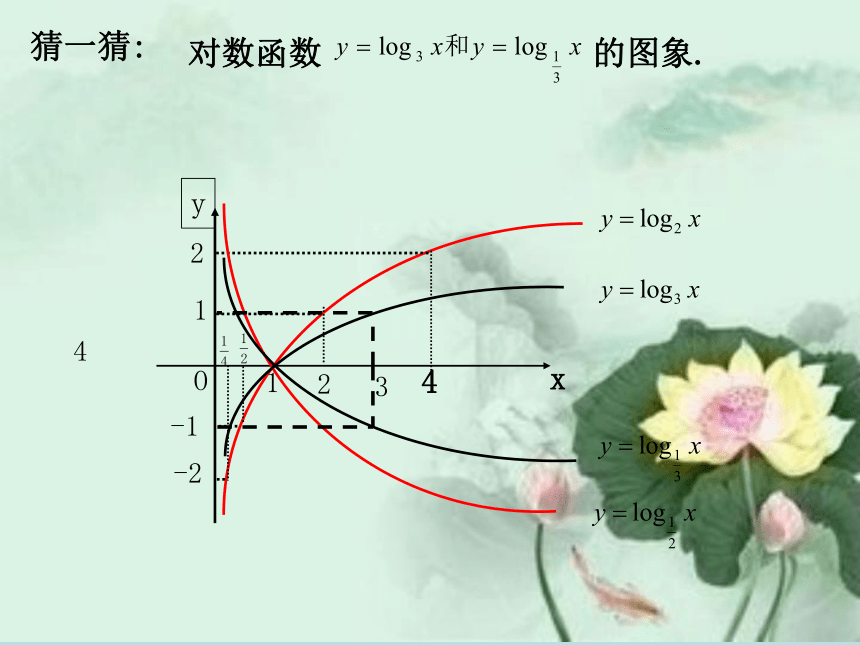
对数函数 的图象.
猜一猜:
2
1
-1
-2
1
2
4
O
y
x
3
4
图 象 性 质
a > 1 0 < a < 1
定义域:
值 域:
过定点:
在(0,+∞)上是
在(0,+∞)上是
对数函数y=logax (a>0,且a≠1) 的图象与性质
(0,+∞)
R
(1,0)
即当x=1时,y=0
增函数
减函数
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
例题
1.求下列函数的定义域:
2.函数y=log2(x-a)的定义域为(1,+∞),
则( )
A.a>1 B.0<a<1 C.a<0 D.a=1
【解析】要使函数y=log2(x-a)的解析式有意义,则x-a>0,即x>a,又因为函数y=log2(x-a)的定义域为(1,+∞),故a=1.
D
对数函数
数形结合
图 象
性 质
定 义
作业布置
P74 第6题 第7题
谢谢!
预习中存在的问题
1.画图不规范
2.对对数函数的定义式理解不够到位
3.求函数的定义域存在问题
学习目标
1.理解对数函数的定义;
2.熟悉对数函数的图象与性质.
我们研究指数函数时,曾讨论过折纸问题,折纸一次,变成两面,折两次,纸变成4面,…,设折x次后,得到纸的面数为y,则
那么,如果知道纸的面数y,如何得到折纸次数x?
y=2x,x∈N*
观察,这个式子有什么特点?
(1)底数为大于0且不等于1的常数,不含有自变量x;
(2) 自变量x在真数位置,且x的系数是1;
(3)log2x的系数是1.
一般地,我们把函数 叫
做对数函数,其中x是自变量,函数的定义域是
探究1:对数函数的定义
y=logax(a>0,且a≠1)
(0,+∞).
1.下列函数是对数函数的是_______.
A
2.对数函数f(x)的图象过点(4,2),求f(x), f(8)
变式训练
解:设对数函数解析式为
因为函数图象过点(4,2)所以 即
得a=2,对数函数解析式为
先画出函数的图象,再借助图象研究其性质
回想一下,我们是如何研究指数函数的?
探究2:对数函数的图象和性质
(1)作y=log2x的图象
…
…
列表
作图步骤: ①列表 ②描点 ③用平滑曲线连接.
描点
连线
2
1
-1
-2
2
4
O
y
x
3
1
同样的方法在同坐标系中作出函数 的图象,并指出二者的关系
描点
连线
2
1
-1
-2
1
2
4
O
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
…
…
…
…
…
…
1
4
对数函数 的图象.
猜一猜:
2
1
-1
-2
1
2
4
O
y
x
3
4
图 象 性 质
a > 1 0 < a < 1
定义域:
值 域:
过定点:
在(0,+∞)上是
在(0,+∞)上是
对数函数y=logax (a>0,且a≠1) 的图象与性质
(0,+∞)
R
(1,0)
即当x=1时,y=0
增函数
减函数
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
例题
1.求下列函数的定义域:
2.函数y=log2(x-a)的定义域为(1,+∞),
则( )
A.a>1 B.0<a<1 C.a<0 D.a=1
【解析】要使函数y=log2(x-a)的解析式有意义,则x-a>0,即x>a,又因为函数y=log2(x-a)的定义域为(1,+∞),故a=1.
D
对数函数
数形结合
图 象
性 质
定 义
作业布置
P74 第6题 第7题
谢谢!
