高中数学人教A版必修1第一章-1.3.1 函数的单调性课件(19张)
文档属性
| 名称 | 高中数学人教A版必修1第一章-1.3.1 函数的单调性课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 15:26:17 | ||
图片预览

文档简介
1.3 函数的基本性质
1.3.1函数的单调性
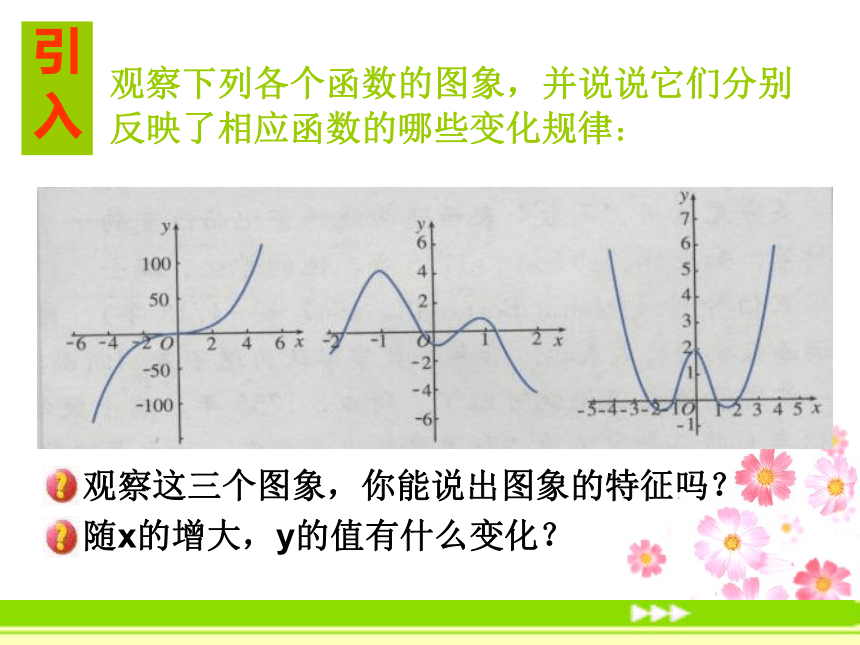
观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
观察这三个图象,你能说出图象的特征吗?
随x的增大,y的值有什么变化?
引 入
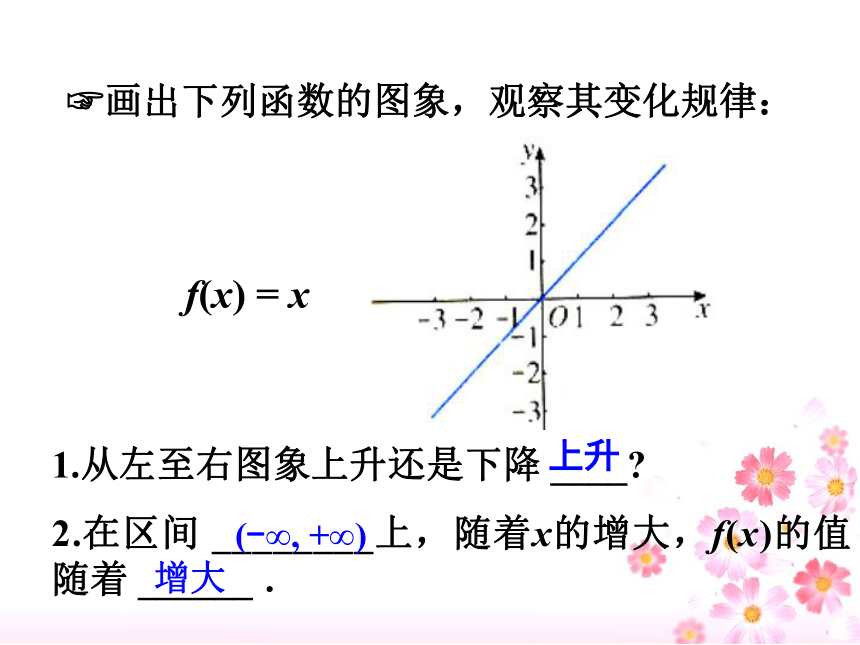
?画出下列函数的图象,观察其变化规律:
1.从左至右图象上升还是下降 ____?
2.在区间 ________上,随着x的增大,f(x)的值随着 ______ .
f(x) = x
(-∞, +∞)
增大
上升
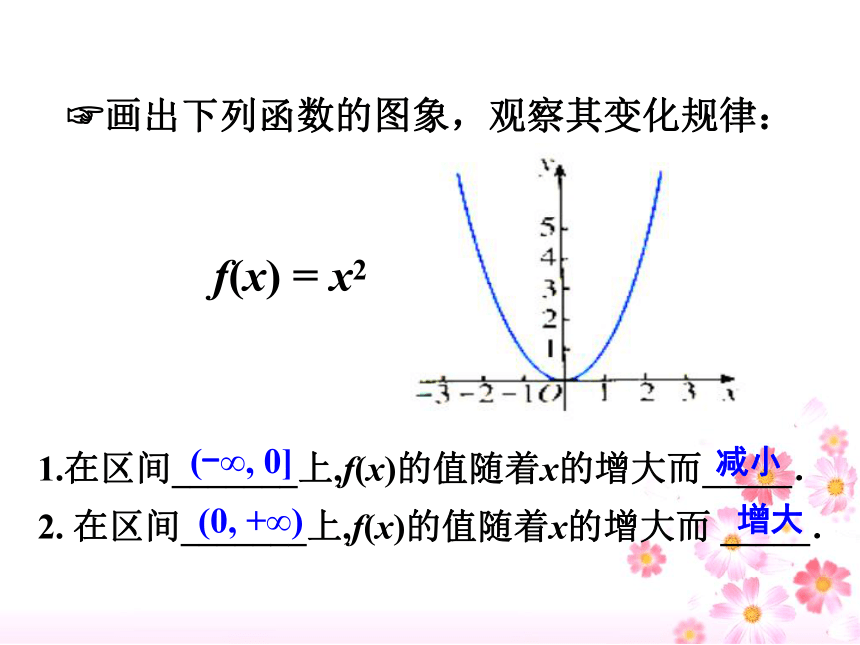
1.在区间_______上,f(x)的值随着x的增大而_____.
2. 在区间_______上,f(x)的值随着x的增大而 _____.
f(x) = x2
(-∞, 0]
(0, +∞)
增大
减小
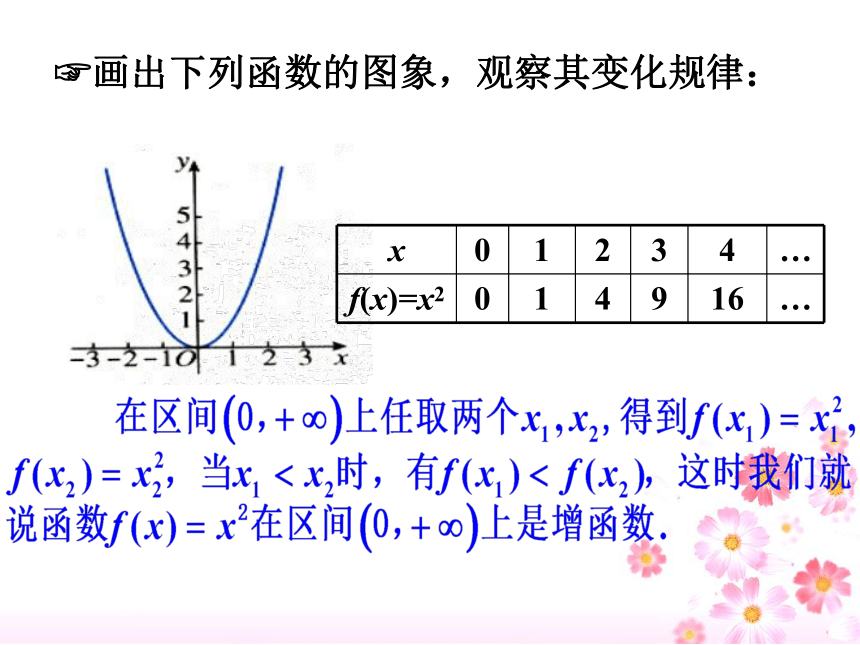
?画出下列函数的图象,观察其变化规律:
x
0
1
2
3
4
…
f(x)=x2
0
1
4
9
16
…
?画出下列函数的图象,观察其变化规律:
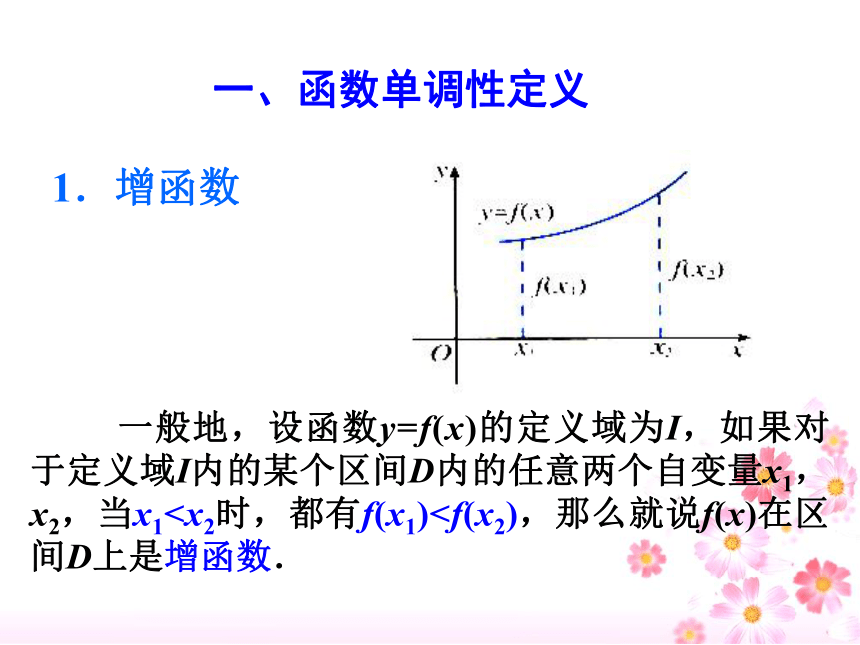
一、函数单调性定义
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x11.增函数
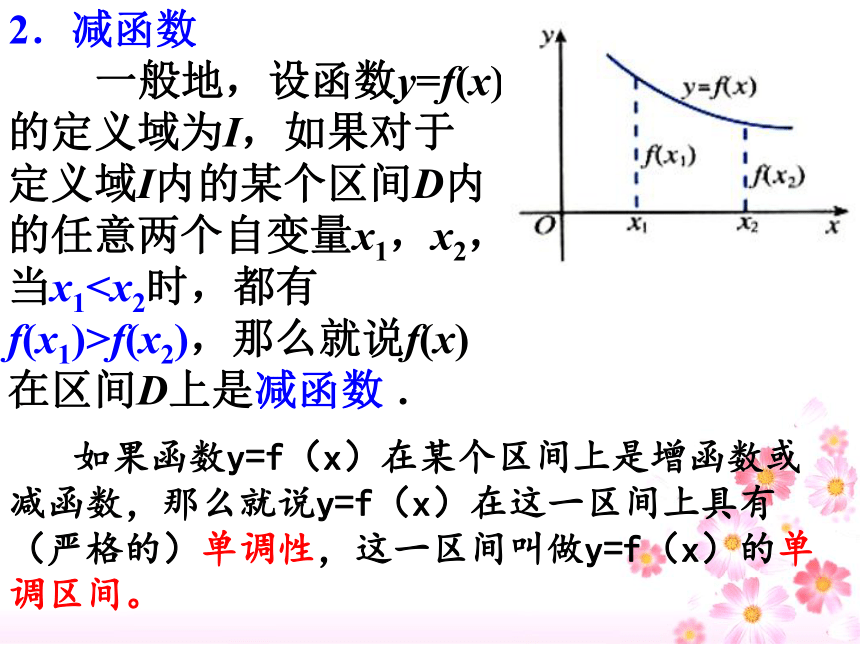
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在区间D上是减函数 .
2.减函数
如果函数y=f(x)在某个区间上是增函数或减函数,那么就说y=f(x)在这一区间上具有(严格的)单调性,这一区间叫做y=f(x)的单调区间。
2.函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;这个区间是定义域的子集。
注意:
1.必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2) 分别是增函数和减函数.
(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则区间为单调递增区间
若函数在此区间上是减函数,则区间为单调递减区间
例1.下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?
解:函数y=f(x)的单调区间有
其中y=f(x)在区间[-5, -2), [1, 3)上是减函数,
在区间[-2, 1), [3, 5] 上是增函数.
[-5, -2), [-2,1), [1, 3), [3, 5].
二.典例精析
课本 32页 练习 第3题
练一练
作图是发现函数单调性的方法之一.
事实证明
思考:如何证明函数的单调性呢?
三、判断函数单调性的方法步骤
①取值: 任取x1,x2∈D,且x1②作差:f(x1)-f(x2);
③化简变形:(因式分解和配方等)乘积或商式;
④判号:(即判断差f(x1)-f(x2)的正负);
⑤下结论:(即指出函数f(x)在给定的区间D上的单调性).
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
分析:利用增(减)函数的定义
例1:证明函数f(x)=3x+2在R上是增函数。
f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)
由x1即 f(x1)证明:设x1,x2是R上的任意两个实数,且x1=3( x1- x2)
于是 f(x1)-f(x2)<0
所以,函数f(x)=3x+2在R上是增函数。
取值
判号
化简变形
作差
下结论
物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1由V1,V2∈ (0,+∞)且V10, V2- V1 >0
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
结论
作差
变形
例2
x
y
设x1,x2是(0,+∞)上的任意两个实数,且x1f(x1)-f(x2)
又由x1即 f(x1) > f(x2)
于是 f(x1)-f(x2) > 0,
由x1、x2∈(0,+∞) ,得 x2 x1 >0
取值
化简
作差
判号
定论
练2.证明:函数 在 上是增函数.
证明:在区间 上任取两个值 ,且
,且
取值
化简
作差
判号
所以,函数 在 上是增函数.
下结论
y
o
x
y
o
x
y
o
x
y
o
x
在
增函数
在
减函数
在
增函数
在
减函数
在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数
在(-∞,+∞)是增函数
在(-∞,0)和(0,+∞)是增函数
y
o
x
o
x
y
四 知识延展
四、归纳小结
3.函数单调性的证明,证明一般分五步:
取 值 → 作 差 → 化简 → 判号 → 下结论
2.会利用函数图像找出函数的单调区间
1.函数单调性的定义
?1.课本32页练习4、5,
P39 习题1.3 A组 第1、2、3题,
2.《3导》练习九,
3.预习课本30~32页内容,并思考什么事函
数的最值?
布置作业
再见
1.3.1函数的单调性
观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
观察这三个图象,你能说出图象的特征吗?
随x的增大,y的值有什么变化?
引 入
?画出下列函数的图象,观察其变化规律:
1.从左至右图象上升还是下降 ____?
2.在区间 ________上,随着x的增大,f(x)的值随着 ______ .
f(x) = x
(-∞, +∞)
增大
上升
1.在区间_______上,f(x)的值随着x的增大而_____.
2. 在区间_______上,f(x)的值随着x的增大而 _____.
f(x) = x2
(-∞, 0]
(0, +∞)
增大
减小
?画出下列函数的图象,观察其变化规律:
x
0
1
2
3
4
…
f(x)=x2
0
1
4
9
16
…
?画出下列函数的图象,观察其变化规律:
一、函数单调性定义
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
2.减函数
如果函数y=f(x)在某个区间上是增函数或减函数,那么就说y=f(x)在这一区间上具有(严格的)单调性,这一区间叫做y=f(x)的单调区间。
2.函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;这个区间是定义域的子集。
注意:
1.必须是对于区间D内的任意两个自变量x1,x2;当x1
(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则区间为单调递增区间
若函数在此区间上是减函数,则区间为单调递减区间
例1.下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?
解:函数y=f(x)的单调区间有
其中y=f(x)在区间[-5, -2), [1, 3)上是减函数,
在区间[-2, 1), [3, 5] 上是增函数.
[-5, -2), [-2,1), [1, 3), [3, 5].
二.典例精析
课本 32页 练习 第3题
练一练
作图是发现函数单调性的方法之一.
事实证明
思考:如何证明函数的单调性呢?
三、判断函数单调性的方法步骤
①取值: 任取x1,x2∈D,且x1
③化简变形:(因式分解和配方等)乘积或商式;
④判号:(即判断差f(x1)-f(x2)的正负);
⑤下结论:(即指出函数f(x)在给定的区间D上的单调性).
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
分析:利用增(减)函数的定义
例1:证明函数f(x)=3x+2在R上是增函数。
f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)
由x1
于是 f(x1)-f(x2)<0
所以,函数f(x)=3x+2在R上是增函数。
取值
判号
化简变形
作差
下结论
物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
结论
作差
变形
例2
x
y
设x1,x2是(0,+∞)上的任意两个实数,且x1
又由x1
于是 f(x1)-f(x2) > 0,
由x1、x2∈(0,+∞) ,得 x2 x1 >0
取值
化简
作差
判号
定论
练2.证明:函数 在 上是增函数.
证明:在区间 上任取两个值 ,且
,且
取值
化简
作差
判号
所以,函数 在 上是增函数.
下结论
y
o
x
y
o
x
y
o
x
y
o
x
在
增函数
在
减函数
在
增函数
在
减函数
在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数
在(-∞,+∞)是增函数
在(-∞,0)和(0,+∞)是增函数
y
o
x
o
x
y
四 知识延展
四、归纳小结
3.函数单调性的证明,证明一般分五步:
取 值 → 作 差 → 化简 → 判号 → 下结论
2.会利用函数图像找出函数的单调区间
1.函数单调性的定义
?1.课本32页练习4、5,
P39 习题1.3 A组 第1、2、3题,
2.《3导》练习九,
3.预习课本30~32页内容,并思考什么事函
数的最值?
布置作业
再见
