高中数学人教A版必修3第一章1.3 算法案例课件(34张PPT)
文档属性
| 名称 | 高中数学人教A版必修3第一章1.3 算法案例课件(34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 205.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 15:49:44 | ||
图片预览











文档简介
1.3算法案例
一、三维目标
(a)知识与技能
1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析。
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序。
(b)过程与方法
在辗转相除法与更相减损术求最大公约数的学习过程中对比我们常见的约分求公因式的方法,比较它们在算法上的区别,并从程序的学习中体会数学的严谨,领会数学算法计算机处理的结合方式,初步掌握把数学算法转化成计算机语言的一般步骤。
案例1 辗转相除法与更相减损术
(c)情感态度与价值观
1.通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献。
2.在学习古代数学家解决数学问题的方法的过程中培养严谨的逻辑思维能力,在利用算法解决数学问题的过程中培养理性的精神和动手实践的能力。
二、教学重难点
重点:理解辗转相除法与更相减损术求最大公约数的方法。
难点:把辗转相除法与更相减损术的方法转换成程序框图与程序语言。
三、学法
在理解最大公约数的基础上去发现辗转相除法与更相减损术中的数学规律,并能模仿已经学过的程序框图与算法语句设计出辗转相除法程序框图与算法程序。
3 5
9 15
[问题1]:在小学,我们已经学过求最大公约数的知识,你能求出18与30的最大公约数吗?
〖创设情景,揭示课题〗
18 30
2
3
∴18和30的最大公约数是2×3=6.
先用两个数公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来.
例:求下面两个正整数的最大公约数:
(1)求25和35的最大公约数
(2)求49和63的最大公约数
25
(1)
5
5
35
7
49
(2)
7
7
63
9
所以,25和35的最大公约数为5
所以,49和63的最大公约数为7
思考:除了用这种方法外还有没有其它方法?
[问题2]:我们都是利用找公约数的方法来求最大公约数,如果公约数比较大而且根据我们的观察又不能得到一些公约数,我们又应该怎样求它们的最大公约数?比如求8251与6105的最大公约数?
〖研探新知〗
1.辗转相除法:
例1 求两个正数8251和6105的最大公约数。
分析:8251与6105两数都比较大,而且没有明显的公约数,如能把它们都变小一点,根据已有的知识即可求出最大公约数.
解:8251=6105×1+2146
显然8251与6105的最大公约数也必是2146的约数,同样6105与2146的公约数也必是8251的约数,所以8251与6105的最大公约数也是6105与2146的最大公约数。
〖研探新知〗
1.辗转相除法:
例1 求两个正数8251和6105的最大公约数。
解:8251=6105×1+2146;
6105=2146×2+1813;
2146=1813×1+333;
1813=333×5+148;
333=148×2+37;
148=37×4+0.
则37为8251与6105的最大公约数。
以上我们求最大公约数的方法就是辗转相除法。也叫欧几里得算法,它是由欧几里得在公元前300年左右首先提出的。
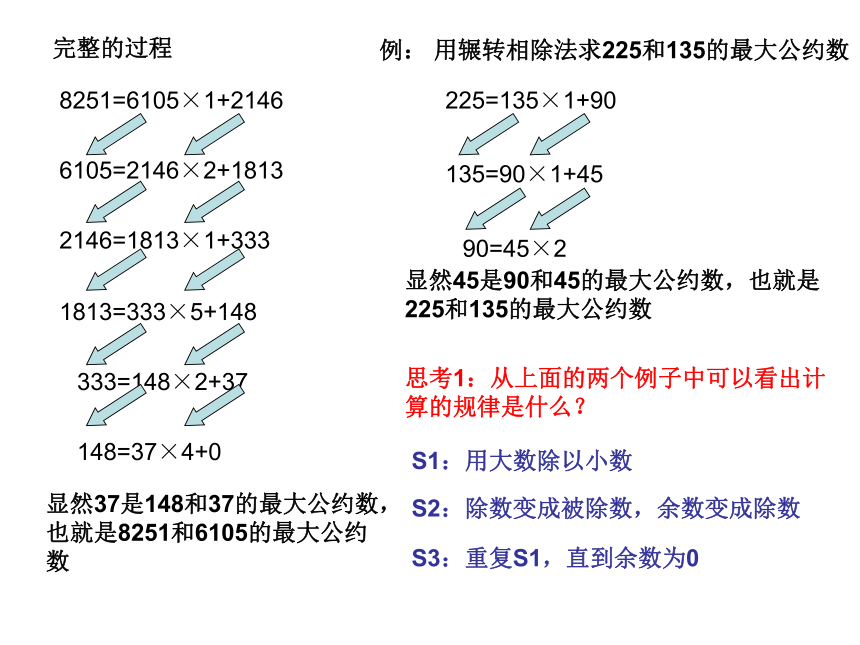
完整的过程
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
例: 用辗转相除法求225和135的最大公约数
225=135×1+90
135=90×1+45
90=45×2
显然37是148和37的最大公约数,也就是8251和6105的最大公约数
显然45是90和45的最大公约数,也就是225和135的最大公约数
思考1:从上面的两个例子中可以看出计算的规律是什么?
S1:用大数除以小数
S2:除数变成被除数,余数变成除数
S3:重复S1,直到余数为0
以上我们求最大公约数的方法就是辗转相除法.也叫欧几里得算法,它是由欧几里得在公元前300年左右首先提出的.利用辗转相除法求最大公约数的。
练习1:利用辗转相除法求两数4081与20723的最大公约数.
(53)
20723=4081×5+318;
4081=318×12+265;
318=265×1+53;
265=53×5+0.
利用辗转相除法求最大公约数的步骤如下:
第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;(m=n×q0+r0)
第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;(n=r0×q1+r1)
第三步:若r1=0,则r0为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;(r0=r1×q2+r2)
……
依次计算直至rn=0,此时所得到的rn-1 即为所求的最大公约数。
思考:你能把辗转相除法编成一个计算机程序吗?
(1) 算法步骤:
第一步:输入两个正整数m,n(m>n).
第二步:计算m除以n所得的余数r.
第三步:m=n,n=r.
第四步:若r=0,则m,n的最大公约数等于m;
否则转到第二步.
第五步:输出最大公约数m.
(2)、程序框图:
开始
输入m,n
r=m MOD n
m=n
r=0?
是
否
n=r
输出m
结束
(3)、程序:
INPUT “m,n=“;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
否
4. 辗转相除法的程序框图及程序:
开始
输入两个正数m,n
mr=m MOD n
r≠0?
输出n
结束
m=x
m=n
n=r
否
是
是
INPUT m,n
IF m x=n
n=m
m=x
END IF
r=m MOD n
WHILE r<>0
m=n
n=r
r=m MOD n
WEND
PRINT n
END
x=n
n=m
2.更相减损术:
我国早期也有解决求最大公约数问题的算法,就是更相减损术。
更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母·子之数,以少减多,更相减损,求其等也,以等数约之。
翻译出来为:第一步:任意给出两个正数;判断它们是否都是偶数。若是,用2约简;若不是,执行第二步。
第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数。继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数。
更相减损术算法步骤:
第四步:输出最大公约数b.
第三步:如果b>r, 那么把b赋给a,把r赋给b;否则把r赋给a,执行第二步;
第二步:把a-b的差赋予r;
第一步:输入两个正整数a,b(a>b,a,b都不是偶数);
例2 用更相减损术求98与63的最大公约数.
解:由于63不是偶数,把98和63以大数减小数,并辗转相减,
即:98-63=35;
63-35=28;
35-28=7;
28-7=21;
21-7=14;
14-7=7.
所以,98与63的最大公约数是7。
练习2:用更相减损术求两个正数84与72的最大公约数。
(12)
3.辗转相除法与更相减损术的比较:
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
(2)辗转相除法算法步骤
第一步:输入两个正整数a,b(a>b);
第二步:把a/b的余数赋给r;
第三步:如果r 0, 那么把b赋给a,把r赋给b,转到第二步;否则转到第四步;
第四步:输出最大公约数b.
案例2 秦九韶算法
一、三维目标
(a)知识与技能
了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
(b)过程与方法
模仿秦九韶计算方法,体会古人计算构思的巧妙.
(c)情感态度与价值观
通过对秦九韶算法的学习,了解中国古代数学家对数学的贡献,充分认识到我国文化历史的悠久。
二、教学重难点
重点:1.秦九韶算法的特点;
难点: 2.秦九韶算法的先进性理解 .
秦九韶(约1202--1261),字道古,四川安岳人。先后在湖北,安徽,江苏,浙江等地做官,1261年左右被贬至梅州,(今广东梅县),不久死于任所。他与李冶,杨辉,朱世杰并称宋元数学四大家。早年在杭州“访习于太史,又尝从隐君子受数学”,1247年写成著名的《数书九章》。《数书九章》全书凡18卷,81题,分为九大类。其最重要的数学成就----“大衍总数术”(一次同余组解法)与“正负开方术"(高次方程数值解法),使这部宋代算经在中世纪世界数学史上占有突出的地位。
〖教学设计〗
[问题1]设计求多项式f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值的算法,并写出程序.
x=5
f=2*x^5-5*x^4-4*x^3+3*x^2-6*x+7
PRINT f
END
程序
点评:上述算法一共做了15次乘法运算,5次加法运算.优点是简单,易懂;缺点是不通用,不能解决任意多项多求值问题,而且计算效率不高.
这析计算上述多项式的值,一共需要9次乘法运算,5次加法运算.
[问题2]有没有更高效的算法?
分析:计算x的幂时,可以利用前面的计算结果,以减少计算量,
即先计算x2,然后依次计算
的值.
第二种做法与第一种做法相比,乘法的运算次数减少了,因而能提高运算效率.而且对于计算机来说,做一次乘法所需的运算时间比做一次加法要长得多,因此第二种做法能更快地得到结果.
[问题3]能否探索更好的算法,来解决任意多项式的求值问题?
f(x)=2x5-5x4-4x3+3x2-6x+7
=(2x4-5x3-4x2+3x-6)x+7
=((2x3-5x2-4x+3)x-6)x+7
=(((2x2-5x-4)x+3)x-6)x+7
=((((2x-5)x-4)x+3)x-6)x+7
v0=2
v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677
所以,当x=5时,多项式的值是2677.
这种求多项式值的方法就叫秦九韶算法.
例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.
解法一:首先将原多项式改写成如下形式 : f(x)=((((2x-5)x-4)x+3)x-6)x+7
v0=2
v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677
所以,当x=5时,多项式的值是2677.
然后由内向外逐层计算一次多项式的值,即
若将x的值代入变形后的式子中,那么求值的计算过程是怎样的?
计算的过程可以列表表示为:
多项式x系数
2
-5
-4
3
-6
7
10
25
105
540
2670
变形后x的"系数"
2
5
21
108
534
2677
f(x) =((((2x-5)x-4)x+3)x-6)x+7, x=5
2 -5 -4 3 -6 7
x=5
10
5
25
21
105
108
540
534
2670
2677
所以,当x=5时,多项式的值是2677.
原多项式的系数
多项式的值.
例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.
解法二:列表
2
2 -5 0 -4 3 -6 0
x=5
10
5
25
25
125
121
605
608
3040
3034
所以,当x=5时,多项式的值是15170.
练一练:用秦九韶算法求多项式 f(x)=2x6-5x5-4x3+3x2-6x当x=5时的值.
解:原多项式先化为:
f(x)=2x6-5x5 +0×x4-4x3+3x2-6x+0
列表
2
15170
15170
注意:n次多项式有n+1项,因此缺少哪一项应将其系数补0.
f(x)=anxn+an-1xn-1+an-2xn-2+……+a1x+a0.
我们可以改写成如下形式:
f(x)=(…(anx+an-1)x+an-2)x+…+a1)x+a0.
求多项式的值时,首先计算最内层括号内一次多项式的值,即
v1=anx+an-1,
然后由内向外逐层计算一次多项式的值,即
一般地,对于一个n次多项式
v2=v1x+an-2,
v3=v2x+an-3, ……,
vn=vn-1x+a0.
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.这种算法称为秦九韶算法.
点评:秦九韶算法是求一元多项式的值的一种方法.
它的特点是:把求一个n次多项式的值转化为求n个一次多项式的值,通过这种转化,把运算的次数由至多n(n+1)/2次乘法运算和n次加法运算,减少为n次乘法运算和n次加法运算,大大提高了运算效率.
v1=anx+an-1,
v2=v1x+an-2,
v3=v2x+an-3, ……,
vn=vn-1x+a0.
观察上述秦九韶算法中的n个一次式,可见vk的计算要用到vk-1的值.
若令v0=an,得
v0=an,
vK=vK-1x+an-k(k=1,2,……,n
这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现.
[问题]画出程序框图,表示用秦九韶算法求5次多项式f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0当x=x0 (x0是任意实数)时的值的过程,然后写出程序.
否
程序框图
开始
输入a0,a1,a2,a3,a4,a5
输入x0
n≤5?
n=1
v=a5
v=vx0+a5-n
n=n+1
输出v
结束
是
INPUT a0,a1,a2,a3,a4,a5
INPUT x0
n=1
v=a5
WHILE n<=5
v=vx0+a5-n
n=n+1
WEND
PRINT v
END
程序
一、三维目标
(a)知识与技能
1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析。
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序。
(b)过程与方法
在辗转相除法与更相减损术求最大公约数的学习过程中对比我们常见的约分求公因式的方法,比较它们在算法上的区别,并从程序的学习中体会数学的严谨,领会数学算法计算机处理的结合方式,初步掌握把数学算法转化成计算机语言的一般步骤。
案例1 辗转相除法与更相减损术
(c)情感态度与价值观
1.通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献。
2.在学习古代数学家解决数学问题的方法的过程中培养严谨的逻辑思维能力,在利用算法解决数学问题的过程中培养理性的精神和动手实践的能力。
二、教学重难点
重点:理解辗转相除法与更相减损术求最大公约数的方法。
难点:把辗转相除法与更相减损术的方法转换成程序框图与程序语言。
三、学法
在理解最大公约数的基础上去发现辗转相除法与更相减损术中的数学规律,并能模仿已经学过的程序框图与算法语句设计出辗转相除法程序框图与算法程序。
3 5
9 15
[问题1]:在小学,我们已经学过求最大公约数的知识,你能求出18与30的最大公约数吗?
〖创设情景,揭示课题〗
18 30
2
3
∴18和30的最大公约数是2×3=6.
先用两个数公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来.
例:求下面两个正整数的最大公约数:
(1)求25和35的最大公约数
(2)求49和63的最大公约数
25
(1)
5
5
35
7
49
(2)
7
7
63
9
所以,25和35的最大公约数为5
所以,49和63的最大公约数为7
思考:除了用这种方法外还有没有其它方法?
[问题2]:我们都是利用找公约数的方法来求最大公约数,如果公约数比较大而且根据我们的观察又不能得到一些公约数,我们又应该怎样求它们的最大公约数?比如求8251与6105的最大公约数?
〖研探新知〗
1.辗转相除法:
例1 求两个正数8251和6105的最大公约数。
分析:8251与6105两数都比较大,而且没有明显的公约数,如能把它们都变小一点,根据已有的知识即可求出最大公约数.
解:8251=6105×1+2146
显然8251与6105的最大公约数也必是2146的约数,同样6105与2146的公约数也必是8251的约数,所以8251与6105的最大公约数也是6105与2146的最大公约数。
〖研探新知〗
1.辗转相除法:
例1 求两个正数8251和6105的最大公约数。
解:8251=6105×1+2146;
6105=2146×2+1813;
2146=1813×1+333;
1813=333×5+148;
333=148×2+37;
148=37×4+0.
则37为8251与6105的最大公约数。
以上我们求最大公约数的方法就是辗转相除法。也叫欧几里得算法,它是由欧几里得在公元前300年左右首先提出的。
完整的过程
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
例: 用辗转相除法求225和135的最大公约数
225=135×1+90
135=90×1+45
90=45×2
显然37是148和37的最大公约数,也就是8251和6105的最大公约数
显然45是90和45的最大公约数,也就是225和135的最大公约数
思考1:从上面的两个例子中可以看出计算的规律是什么?
S1:用大数除以小数
S2:除数变成被除数,余数变成除数
S3:重复S1,直到余数为0
以上我们求最大公约数的方法就是辗转相除法.也叫欧几里得算法,它是由欧几里得在公元前300年左右首先提出的.利用辗转相除法求最大公约数的。
练习1:利用辗转相除法求两数4081与20723的最大公约数.
(53)
20723=4081×5+318;
4081=318×12+265;
318=265×1+53;
265=53×5+0.
利用辗转相除法求最大公约数的步骤如下:
第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;(m=n×q0+r0)
第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;(n=r0×q1+r1)
第三步:若r1=0,则r0为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;(r0=r1×q2+r2)
……
依次计算直至rn=0,此时所得到的rn-1 即为所求的最大公约数。
思考:你能把辗转相除法编成一个计算机程序吗?
(1) 算法步骤:
第一步:输入两个正整数m,n(m>n).
第二步:计算m除以n所得的余数r.
第三步:m=n,n=r.
第四步:若r=0,则m,n的最大公约数等于m;
否则转到第二步.
第五步:输出最大公约数m.
(2)、程序框图:
开始
输入m,n
r=m MOD n
m=n
r=0?
是
否
n=r
输出m
结束
(3)、程序:
INPUT “m,n=“;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
否
4. 辗转相除法的程序框图及程序:
开始
输入两个正数m,n
m
r≠0?
输出n
结束
m=x
m=n
n=r
否
是
是
INPUT m,n
IF m
n=m
m=x
END IF
r=m MOD n
WHILE r<>0
m=n
n=r
r=m MOD n
WEND
PRINT n
END
x=n
n=m
2.更相减损术:
我国早期也有解决求最大公约数问题的算法,就是更相减损术。
更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母·子之数,以少减多,更相减损,求其等也,以等数约之。
翻译出来为:第一步:任意给出两个正数;判断它们是否都是偶数。若是,用2约简;若不是,执行第二步。
第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数。继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数。
更相减损术算法步骤:
第四步:输出最大公约数b.
第三步:如果b>r, 那么把b赋给a,把r赋给b;否则把r赋给a,执行第二步;
第二步:把a-b的差赋予r;
第一步:输入两个正整数a,b(a>b,a,b都不是偶数);
例2 用更相减损术求98与63的最大公约数.
解:由于63不是偶数,把98和63以大数减小数,并辗转相减,
即:98-63=35;
63-35=28;
35-28=7;
28-7=21;
21-7=14;
14-7=7.
所以,98与63的最大公约数是7。
练习2:用更相减损术求两个正数84与72的最大公约数。
(12)
3.辗转相除法与更相减损术的比较:
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
(2)辗转相除法算法步骤
第一步:输入两个正整数a,b(a>b);
第二步:把a/b的余数赋给r;
第三步:如果r 0, 那么把b赋给a,把r赋给b,转到第二步;否则转到第四步;
第四步:输出最大公约数b.
案例2 秦九韶算法
一、三维目标
(a)知识与技能
了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
(b)过程与方法
模仿秦九韶计算方法,体会古人计算构思的巧妙.
(c)情感态度与价值观
通过对秦九韶算法的学习,了解中国古代数学家对数学的贡献,充分认识到我国文化历史的悠久。
二、教学重难点
重点:1.秦九韶算法的特点;
难点: 2.秦九韶算法的先进性理解 .
秦九韶(约1202--1261),字道古,四川安岳人。先后在湖北,安徽,江苏,浙江等地做官,1261年左右被贬至梅州,(今广东梅县),不久死于任所。他与李冶,杨辉,朱世杰并称宋元数学四大家。早年在杭州“访习于太史,又尝从隐君子受数学”,1247年写成著名的《数书九章》。《数书九章》全书凡18卷,81题,分为九大类。其最重要的数学成就----“大衍总数术”(一次同余组解法)与“正负开方术"(高次方程数值解法),使这部宋代算经在中世纪世界数学史上占有突出的地位。
〖教学设计〗
[问题1]设计求多项式f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值的算法,并写出程序.
x=5
f=2*x^5-5*x^4-4*x^3+3*x^2-6*x+7
PRINT f
END
程序
点评:上述算法一共做了15次乘法运算,5次加法运算.优点是简单,易懂;缺点是不通用,不能解决任意多项多求值问题,而且计算效率不高.
这析计算上述多项式的值,一共需要9次乘法运算,5次加法运算.
[问题2]有没有更高效的算法?
分析:计算x的幂时,可以利用前面的计算结果,以减少计算量,
即先计算x2,然后依次计算
的值.
第二种做法与第一种做法相比,乘法的运算次数减少了,因而能提高运算效率.而且对于计算机来说,做一次乘法所需的运算时间比做一次加法要长得多,因此第二种做法能更快地得到结果.
[问题3]能否探索更好的算法,来解决任意多项式的求值问题?
f(x)=2x5-5x4-4x3+3x2-6x+7
=(2x4-5x3-4x2+3x-6)x+7
=((2x3-5x2-4x+3)x-6)x+7
=(((2x2-5x-4)x+3)x-6)x+7
=((((2x-5)x-4)x+3)x-6)x+7
v0=2
v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677
所以,当x=5时,多项式的值是2677.
这种求多项式值的方法就叫秦九韶算法.
例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.
解法一:首先将原多项式改写成如下形式 : f(x)=((((2x-5)x-4)x+3)x-6)x+7
v0=2
v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677
所以,当x=5时,多项式的值是2677.
然后由内向外逐层计算一次多项式的值,即
若将x的值代入变形后的式子中,那么求值的计算过程是怎样的?
计算的过程可以列表表示为:
多项式x系数
2
-5
-4
3
-6
7
10
25
105
540
2670
变形后x的"系数"
2
5
21
108
534
2677
f(x) =((((2x-5)x-4)x+3)x-6)x+7, x=5
2 -5 -4 3 -6 7
x=5
10
5
25
21
105
108
540
534
2670
2677
所以,当x=5时,多项式的值是2677.
原多项式的系数
多项式的值.
例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.
解法二:列表
2
2 -5 0 -4 3 -6 0
x=5
10
5
25
25
125
121
605
608
3040
3034
所以,当x=5时,多项式的值是15170.
练一练:用秦九韶算法求多项式 f(x)=2x6-5x5-4x3+3x2-6x当x=5时的值.
解:原多项式先化为:
f(x)=2x6-5x5 +0×x4-4x3+3x2-6x+0
列表
2
15170
15170
注意:n次多项式有n+1项,因此缺少哪一项应将其系数补0.
f(x)=anxn+an-1xn-1+an-2xn-2+……+a1x+a0.
我们可以改写成如下形式:
f(x)=(…(anx+an-1)x+an-2)x+…+a1)x+a0.
求多项式的值时,首先计算最内层括号内一次多项式的值,即
v1=anx+an-1,
然后由内向外逐层计算一次多项式的值,即
一般地,对于一个n次多项式
v2=v1x+an-2,
v3=v2x+an-3, ……,
vn=vn-1x+a0.
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.这种算法称为秦九韶算法.
点评:秦九韶算法是求一元多项式的值的一种方法.
它的特点是:把求一个n次多项式的值转化为求n个一次多项式的值,通过这种转化,把运算的次数由至多n(n+1)/2次乘法运算和n次加法运算,减少为n次乘法运算和n次加法运算,大大提高了运算效率.
v1=anx+an-1,
v2=v1x+an-2,
v3=v2x+an-3, ……,
vn=vn-1x+a0.
观察上述秦九韶算法中的n个一次式,可见vk的计算要用到vk-1的值.
若令v0=an,得
v0=an,
vK=vK-1x+an-k(k=1,2,……,n
这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现.
[问题]画出程序框图,表示用秦九韶算法求5次多项式f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0当x=x0 (x0是任意实数)时的值的过程,然后写出程序.
否
程序框图
开始
输入a0,a1,a2,a3,a4,a5
输入x0
n≤5?
n=1
v=a5
v=vx0+a5-n
n=n+1
输出v
结束
是
INPUT a0,a1,a2,a3,a4,a5
INPUT x0
n=1
v=a5
WHILE n<=5
v=vx0+a5-n
n=n+1
WEND
PRINT v
END
程序
