高中数学人教A版必修5第三章:3.3.1二元一次不等式(组)与平面区域(2课时)课件(18张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第三章:3.3.1二元一次不等式(组)与平面区域(2课时)课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览


文档简介
3.3.1
二元一次不等式(组)与平面区域
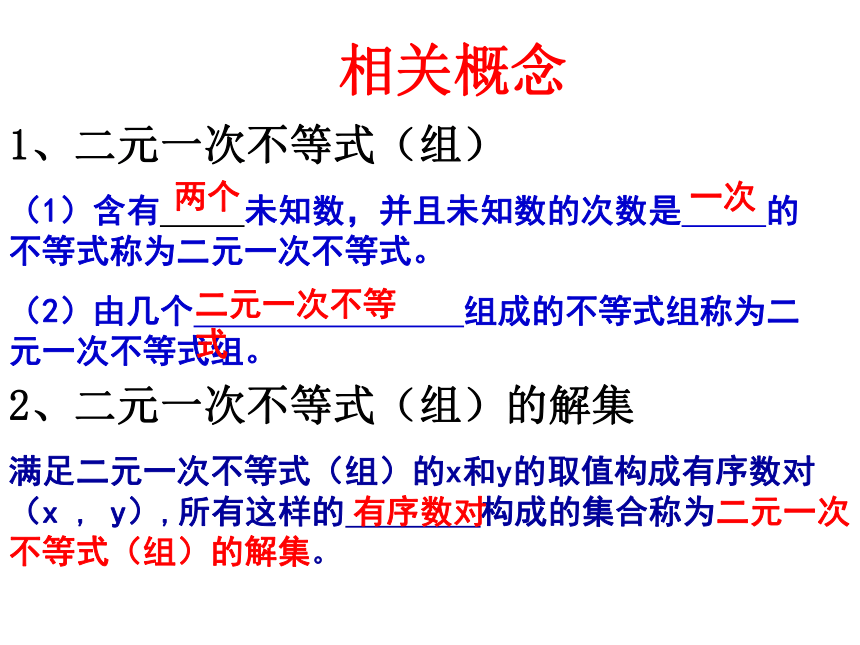
1、二元一次不等式(组)
(1)含有 未知数,并且未知数的次数是 的 不等式称为二元一次不等式。
(2)由几个 组成的不等式组称为二元一次不等式组。
相关概念
2、二元一次不等式(组)的解集
满足二元一次不等式(组)的x和y的取值构成有序数对 (x , y),所有这样的 构成的集合称为二元一次不等式(组)的解集。
二元一次不等式
两个
一次
有序数对
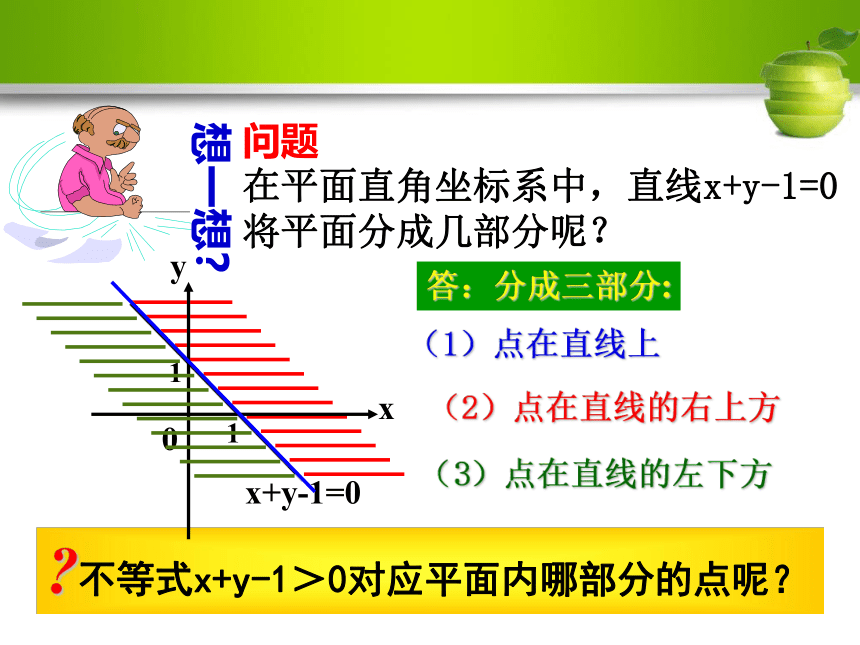
问题
在平面直角坐标系中,直线x+y-1=0将平面分成几部分呢?
?不等式x+y-1>0对应平面内哪部分的点呢?
答:分成三部分:
(2)点在直线的右上方
(3)点在直线的左下方
0
x
y
1
1
x+y-1=0
想一想?
(1)点在直线上
右上方点
左下方点
区域内的点
x+y-1值的正负
代入点的坐标
(1,1)
(2,0)
(0,0)
(2,1)
(-1,1)
(-1,0)
(-1,-1)
(2,2)
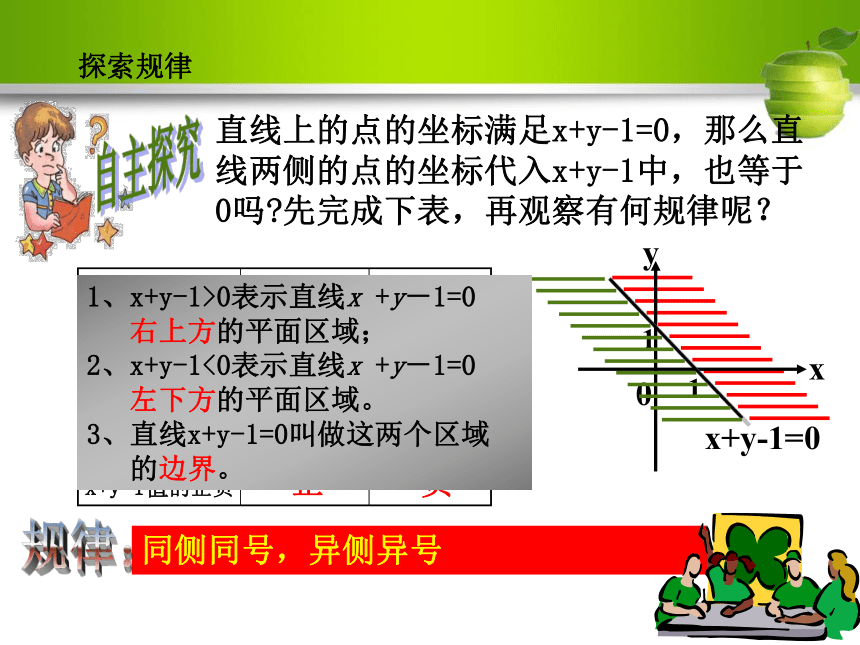
直线上的点的坐标满足x+y-1=0,那么直线两侧的点的坐标代入x+y-1中,也等于0吗?先完成下表,再观察有何规律呢?
探索规律
自主探究
0
x
y
1
1
x+y-1=0
同侧同号,异侧异号
规律:
正
负
1、x+y-1>0表示直线x +y-1=0
右上方的平面区域;
2、x+y-1<0表示直线x +y-1=0
左下方的平面区域。
3、直线x+y-1=0叫做这两个区域
的边界。
一般地,在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域,我们把直线画成虚线,以表示区域不包含边界;不等式 Ax+By+C≥0表示的平面区域包括边界,把边界画成实线。
1、
由于直线同侧的点的坐标代入Ax+By+C中,所得实数符号相同,所以只需在直线的某一侧取一个特殊点代入Ax+By+C中,从所得结果的正负即可判断Ax+By+C>0表示哪一侧的区域。
2、
方法总结:
画二元一次不等式表示的平面区域的步骤:
1、线定界(注意边界的虚实)
2、点定域(代入特殊点验证)
C≠0时,常把原点(0,0)作为特殊点;
C=0时,可取其他特殊点。
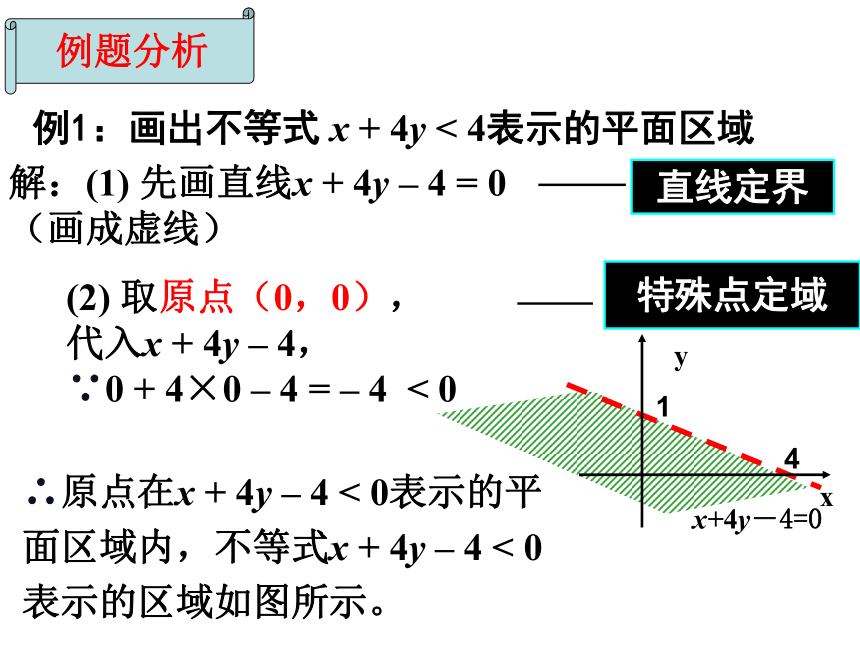
例1:画出不等式 x + 4y < 4表示的平面区域
x+4y―4=0
解:(1) 先画直线x + 4y – 4 = 0 (画成虚线)
(2) 取原点(0,0),
代入x + 4y – 4,
∵0 + 4×0 – 4 = – 4 < 0
∴原点在x + 4y – 4 < 0表示的平面区域内,不等式x + 4y – 4 < 0
表示的区域如图所示。
x
y
1
4
直线定界
特殊点定域
例题分析
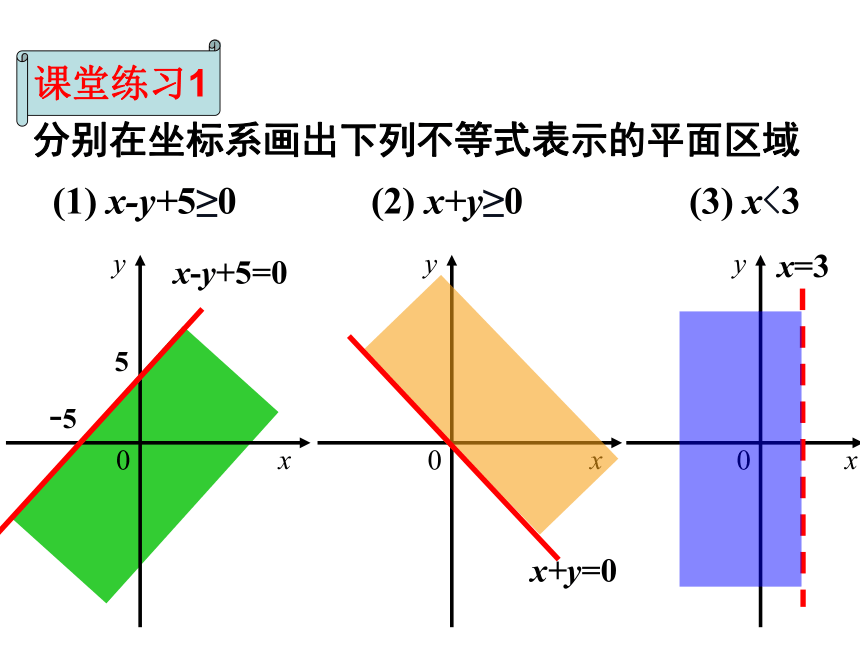
分别在坐标系画出下列不等式表示的平面区域
(1) x-y+5≥0
(2) x+y≥0
(3) x<3
0
x
y
x-y+5=0
-5
5
0
x
y
x+y=0
0
x
y
x=3
课堂练习1
O
x
y
x+y=0
x=3
x-y+5=0
-5
5
例2:画出不等式组
表示的平面区域.
例题分析
分析:不等式组表示的平面区域是各不等式所表示平面区域的公共部分。
此区域为所求
1、不等式x – 2y + 6 > 0表示的区域在直线
x – 2y + 6 = 0的( )
A.右上方 B.右下方 C.左上方 D.左下方
2、不等式3x + 2y – 6 ≤0表示的平面区域是( )
B
D
课本P86 1、2、3
课堂练习2
3、不等式组
B
表示的平面区域是( )
作业布置
P93 A组第1、2题
B组第1题
1、二元一次不等式Ax+By+C>0(或<0)在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点
组成的平面区域。
2、二元一次不等式表示直线哪一侧平面区域的
判断方法:
直线定界,特殊点定域。
C≠0时,取原点作特殊点;
C=0时,取其他特殊点。
注意:(1)画图时应非常准确,否则将得不到正确结果。
(2)
若区域包括边界, 则把边界画成实线;
若区域不包括边界,则把边界画成虚线。
小结
能力提升
1、如图,表示满足不等式(x-y)(x+2y-2)>0的点(x,y)所在区域应为:( )
B
y
1
2
χ
O
(C)
y
1
2
χ
O
(D)
y
1
2
χ
O
(A)
y
1
2
χ
O
(B)
(0,1)
(-4,-1)
(2,-1)
x
y
2、写出表示下面区域的二元一次不等式组
题型:根据平面区域写出二元一次不等式(组)
解析:边界直线方程为
x+y-1=0
代入原点(0,0)
得0+0-1<0
即所求不等式为
x+y-1≤0
x
y
-2
o
1
1
-1
x-2y+2>0
y≥-1
青色区域
蓝色区域
x-2y+2>0
y≥-1
x+y-1≤0
x+y-1≤0
粉红色区域
黄色区域
2、写出表示下面区域的二元一次不等式组
解析:
由于在异侧,则(1,2)和(1,1)
代入3x-y+m 所得数值异号,
则有(3-2+m)(3-1+m)<0
所以(m+1)(m+2) <0
即:-2试确定m的范围,使点(1,2)和(1,1)在3x-y+m=0的异侧。
3、
变式:若在同侧,m的范围又是什么呢?
解析:
由于在同侧,则(1,2)和(1,1)
代入3x-y+m 所得数值同号,
则有(3-2+m)(3-1+m)> 0
所以(m+1)(m+2)> 0
即:m <-2或m>-1
求二元一次不等式组
所表示的平面区域的面积
4、
x-y+5≥0
y≥2
0≤x≤2
2
x
o
y
-5
5
D
C
B
A
x-y+5=0
x=2
y=2
2
如图,平面区域为直角梯形,易得A(0,2),B(2,2),C(2,7),D(0,5)
所以AD=3,AB=2,BC=5
故所求区域的面积为
S=
解析:
若二元一次不等式组
所表示的平面区域是一个三角形,求a的取值范围
变式:
x-y+5≥0
y≥a
0≤x≤2
2
x
o
y
5
D
C
x-y+5=0
x=2
-5
y=a
y=a
y=a
y=5
y=7
7
数形结合思想
答案:5≤a<7
二元一次不等式(组)与平面区域
1、二元一次不等式(组)
(1)含有 未知数,并且未知数的次数是 的 不等式称为二元一次不等式。
(2)由几个 组成的不等式组称为二元一次不等式组。
相关概念
2、二元一次不等式(组)的解集
满足二元一次不等式(组)的x和y的取值构成有序数对 (x , y),所有这样的 构成的集合称为二元一次不等式(组)的解集。
二元一次不等式
两个
一次
有序数对
问题
在平面直角坐标系中,直线x+y-1=0将平面分成几部分呢?
?不等式x+y-1>0对应平面内哪部分的点呢?
答:分成三部分:
(2)点在直线的右上方
(3)点在直线的左下方
0
x
y
1
1
x+y-1=0
想一想?
(1)点在直线上
右上方点
左下方点
区域内的点
x+y-1值的正负
代入点的坐标
(1,1)
(2,0)
(0,0)
(2,1)
(-1,1)
(-1,0)
(-1,-1)
(2,2)
直线上的点的坐标满足x+y-1=0,那么直线两侧的点的坐标代入x+y-1中,也等于0吗?先完成下表,再观察有何规律呢?
探索规律
自主探究
0
x
y
1
1
x+y-1=0
同侧同号,异侧异号
规律:
正
负
1、x+y-1>0表示直线x +y-1=0
右上方的平面区域;
2、x+y-1<0表示直线x +y-1=0
左下方的平面区域。
3、直线x+y-1=0叫做这两个区域
的边界。
一般地,在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域,我们把直线画成虚线,以表示区域不包含边界;不等式 Ax+By+C≥0表示的平面区域包括边界,把边界画成实线。
1、
由于直线同侧的点的坐标代入Ax+By+C中,所得实数符号相同,所以只需在直线的某一侧取一个特殊点代入Ax+By+C中,从所得结果的正负即可判断Ax+By+C>0表示哪一侧的区域。
2、
方法总结:
画二元一次不等式表示的平面区域的步骤:
1、线定界(注意边界的虚实)
2、点定域(代入特殊点验证)
C≠0时,常把原点(0,0)作为特殊点;
C=0时,可取其他特殊点。
例1:画出不等式 x + 4y < 4表示的平面区域
x+4y―4=0
解:(1) 先画直线x + 4y – 4 = 0 (画成虚线)
(2) 取原点(0,0),
代入x + 4y – 4,
∵0 + 4×0 – 4 = – 4 < 0
∴原点在x + 4y – 4 < 0表示的平面区域内,不等式x + 4y – 4 < 0
表示的区域如图所示。
x
y
1
4
直线定界
特殊点定域
例题分析
分别在坐标系画出下列不等式表示的平面区域
(1) x-y+5≥0
(2) x+y≥0
(3) x<3
0
x
y
x-y+5=0
-5
5
0
x
y
x+y=0
0
x
y
x=3
课堂练习1
O
x
y
x+y=0
x=3
x-y+5=0
-5
5
例2:画出不等式组
表示的平面区域.
例题分析
分析:不等式组表示的平面区域是各不等式所表示平面区域的公共部分。
此区域为所求
1、不等式x – 2y + 6 > 0表示的区域在直线
x – 2y + 6 = 0的( )
A.右上方 B.右下方 C.左上方 D.左下方
2、不等式3x + 2y – 6 ≤0表示的平面区域是( )
B
D
课本P86 1、2、3
课堂练习2
3、不等式组
B
表示的平面区域是( )
作业布置
P93 A组第1、2题
B组第1题
1、二元一次不等式Ax+By+C>0(或<0)在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点
组成的平面区域。
2、二元一次不等式表示直线哪一侧平面区域的
判断方法:
直线定界,特殊点定域。
C≠0时,取原点作特殊点;
C=0时,取其他特殊点。
注意:(1)画图时应非常准确,否则将得不到正确结果。
(2)
若区域包括边界, 则把边界画成实线;
若区域不包括边界,则把边界画成虚线。
小结
能力提升
1、如图,表示满足不等式(x-y)(x+2y-2)>0的点(x,y)所在区域应为:( )
B
y
1
2
χ
O
(C)
y
1
2
χ
O
(D)
y
1
2
χ
O
(A)
y
1
2
χ
O
(B)
(0,1)
(-4,-1)
(2,-1)
x
y
2、写出表示下面区域的二元一次不等式组
题型:根据平面区域写出二元一次不等式(组)
解析:边界直线方程为
x+y-1=0
代入原点(0,0)
得0+0-1<0
即所求不等式为
x+y-1≤0
x
y
-2
o
1
1
-1
x-2y+2>0
y≥-1
青色区域
蓝色区域
x-2y+2>0
y≥-1
x+y-1≤0
x+y-1≤0
粉红色区域
黄色区域
2、写出表示下面区域的二元一次不等式组
解析:
由于在异侧,则(1,2)和(1,1)
代入3x-y+m 所得数值异号,
则有(3-2+m)(3-1+m)<0
所以(m+1)(m+2) <0
即:-2
3、
变式:若在同侧,m的范围又是什么呢?
解析:
由于在同侧,则(1,2)和(1,1)
代入3x-y+m 所得数值同号,
则有(3-2+m)(3-1+m)> 0
所以(m+1)(m+2)> 0
即:m <-2或m>-1
求二元一次不等式组
所表示的平面区域的面积
4、
x-y+5≥0
y≥2
0≤x≤2
2
x
o
y
-5
5
D
C
B
A
x-y+5=0
x=2
y=2
2
如图,平面区域为直角梯形,易得A(0,2),B(2,2),C(2,7),D(0,5)
所以AD=3,AB=2,BC=5
故所求区域的面积为
S=
解析:
若二元一次不等式组
所表示的平面区域是一个三角形,求a的取值范围
变式:
x-y+5≥0
y≥a
0≤x≤2
2
x
o
y
5
D
C
x-y+5=0
x=2
-5
y=a
y=a
y=a
y=5
y=7
7
数形结合思想
答案:5≤a<7
