高中数学人教A版必修5第三章:3.3.2简单线性规划(2课时)课件(31张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第三章:3.3.2简单线性规划(2课时)课件(31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 494.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 15:55:36 | ||
图片预览










文档简介
3.3.2简单线性规划问题
第一课时
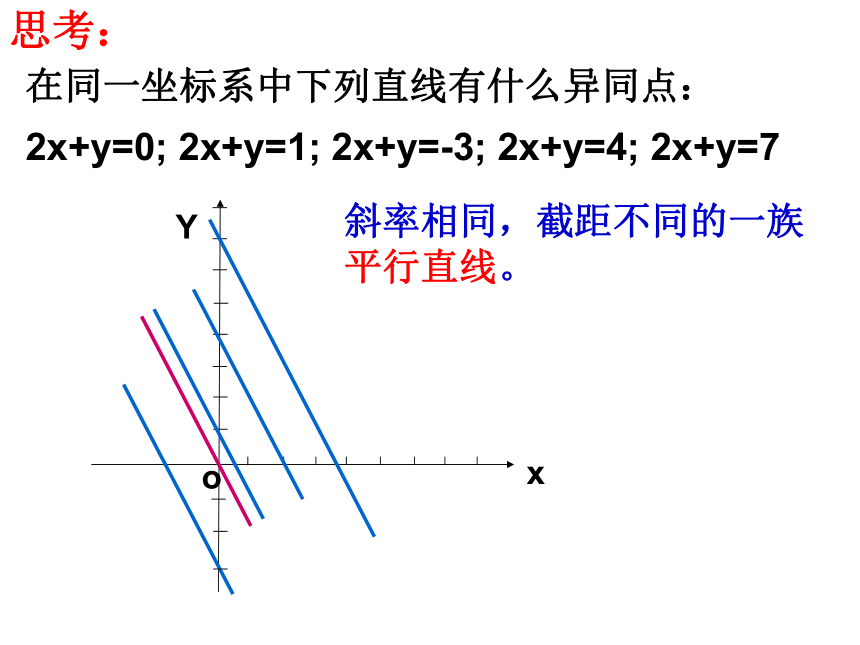
2x+y=0; 2x+y=1; 2x+y=-3; 2x+y=4; 2x+y=7
x
Y
o
斜率相同,截距不同的一族平行直线。
思考:
在同一坐标系中下列直线有什么异同点:
问题1:
某工厂用A,B两种配件生产甲,乙两种产品,
每生产一件甲种产品使用4个A配件耗时1h,
每生产一件乙种产品使用4个B配件耗时2h,
该厂每天最多可从配件厂获得16个A配件和
12个B配件,按每天工作8小时计算,该厂所有
可能的日生产安排是什么?
若生产1件甲种产品获利2万元,生产1 件乙
种产品获利3万元,采用哪种生产安排利润最大?
3
2
利润(万元)
8
2
1
所需时间
12
4
—
B种配件
16
—
4
A种配件
资源限额
乙产品
(1件)
甲产品
(1件)
产品
消 耗 量
资 源
把问题1的有关数据列表表示如下:
设甲,乙两种产品分别生产x, y件,
0
x
y
4
3
4
8
将上面不等式组表示成平面上的区域,区域内
所有坐标为整数的点P(x,y),安排生产任务x,y
都是有意义的.
设甲,乙两种产品分别生产x,y件,由己知条件可得:
问题:求利润2x+3y的最大值.
若设利润为z,则z=2x+3y,这样上述问题转化为:
当x,y在满足上述约束条件时,z的最大值为多少?
当点P在可允许的取值范围变化时,
0
x
y
4
3
4
8
M(4,2)
问题:求利润z=2x+3y的最大值.
象这样关于x,y一次不等
式组的约束条件称为
线性约束条件
Z=2x+3y称为目标函数,(因这里
目标函数为关于x,y的一次式,又
称为线性目标函数
在线性约束下求线性目标函数
的最值问题,统称为线性规划,
满足线性约束的解(x,y)叫做可行解,
所有可行解组成的集合叫做可行域
使目标函数取得最值的可行解叫做这个
问题的最优解
变式:若生产一件甲产品获利1万元,
生产一件乙产品获利3万元,采用哪种
生产安排利润最大?
0
x
y
4
3
4
8
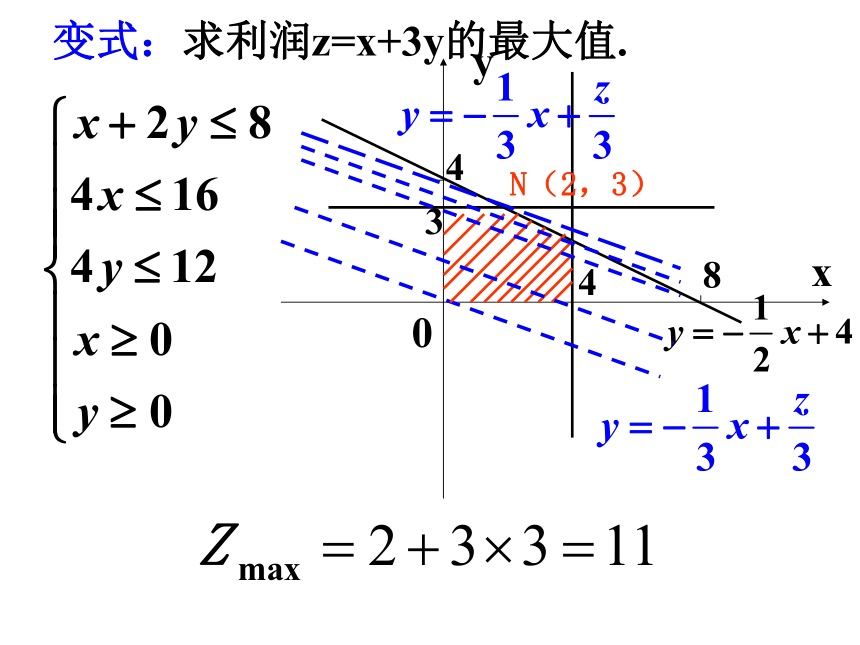
N(2,3)
变式:求利润z=x+3y的最大值.
解线性规划问题的步骤:
(2)移:在线性目标函数所表示的一组平行线 中,利用平移的方法找出与可行域有公共点且
截距最大或最小的直线
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
P91:练习
1(1)求z=2x+y的最值,使式中的x、y满足约束条件:
x
O
y
A
B
C
y=x
x+y=1
y=-1
2x+y=0
B:(-1,-1)
C:(2,-1)
Z min=-3
Zmax=3
目标函数: Z=2x+y
小 结
本节主要学习了线性约束下如何求目
标函数的最值问题
正确列出变量的不等关系式,准确作出
可行域是解决目标函数最值的关健
线性目标函数的最值一般都是在可行域
的顶点或边界取得.
把目标函数转化为某一直线,其斜率与
可行域边界所在直线斜率的大小关系一定要
弄清楚.
3.3.2简单线性规划问题
第二课时
一、复习概念
把求最大值或求最小值的的函数称为目标函数,因为它是关于变量x、y的一次解析式,又称线性目标函数。
满足线性约束的解
(x,y)叫做可行解。
y
x
4
8
4
3
o
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
一组关于变量x、y的一次不等式,称为线性约束条件
由所有可行解组成的集合叫做可行域。
使目标函数取得最大值或最小值的可行解叫做这个问题的最优解。
可行域
可行解
最优解
二.回顾解线性规划问题的步骤
(2)移:在线性目标函数所表示的一组平行线 中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
P91:练习
1(1)求z=2x+y的最值,使式中的x、y满足约束条件:
x
O
y
A
B
C
y=x
x+y=1
y=-1
2x+y=0
B:(-1,-1)
C:(2,-1)
Z min=-3
Zmax=3
目标函数: Z=2x+y
例6、要将两种大小不同规格的钢板截成A、 B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 :
规格类型
钢板类型
第一种钢板
第二种钢板
A规格
B规格
C规格
2
1
2
1
3
1
今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。
解:设需截第一种钢板x张、第二种钢板y张,可得
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
2x+y≥15,
{
x+2y≥18,
x+3y≥27,
x≥0, x∈N*
y≥0 y∈N*
经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.
答:(略)
作出一组平行直线z= x+y,
目标函数z=x+y
B(3,9)
C(4,8)
A(18/5,39/5)
打网格线法
在可行域内打出网格线,
当直线经过点A时z=x+y=11.4,但它不是最优整数解,
将直线x+y=11.4继续向上平移,
2x+y=15
x+3y=27
x+2y=18
x+y =0
直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.
所以Z min=12
作出一组平行直线z = x+y,
目标函数
z = x+y
B(3,9)
C(4,8)
A(18/5,39/5)
当直线经过点A时z=x+y=11.4,但它不是最优整数解.
x+y=12
调整优值法
2x+y≥15,
{
x+2y≥18,
x+3y≥27,
x≥0, x∈N*
y≥0 y∈N*
x
0
y
在可行域内找出最优解、线性规划整数解问题的一般方法是:
1.若区域“顶点”处恰好为整点,那么它就是最优解;(在包括边界的情况下)
2.若区域“顶点”不是整点或不包括边界时,应先求出该点坐标,并计算目标函数值Z,然后在可行域内适当放缩目标函数值,使它为整数,且与Z最接近,在这条对应的直线中,取可行域内整点,如果没有整点,继续放缩,直至取到整点为止。 (调整优值法)
3.在可行域内找整数解,一般采用平移找解法,即打网络、找整点、平移直线、找出整数最优解
例7:一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t、硝酸盐18t;生产1车皮乙种肥料需要的主要原料是磷酸盐1t、硝酸盐15t。现库存磷酸盐10t、硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域。并计算生产甲、乙两种肥料各多少车皮,能够产生最大的利润?
解:设x、y分别为计划生产甲、乙两种混合
肥料的车皮数,于是满足以下条件:
x
y
o
解:设生产甲种肥料x车皮、乙种肥料y车皮,能够产生利润Z万元。目标函数为Z=x+0.5y,可行域如图:
把Z=x+0.5y变形为y=-2x+2z,它表示斜率为-2,在y轴上的截距为2z的一组直线系。
x
y
o
由图可以看出,当直线经过可行域上的点M时,
截距2z最大,即z最大。
答:生产甲种、乙种肥料各2车皮,能够产生最大利润,最大利润为3万元。
M
容易求得M点的坐标为(2,2),则Zmax=3
作业布置
课本 P91 :
第1(2)、2题
小 结:
二元一次不等式
表示平面区域
直线定界,
特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:画、移、求、答
P91 练习 2
某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元、2000元,甲、乙产品都需要在A、B两种设备上加工,在每台A、B上加工1件甲所需工时分别为1h、2h,加工1件乙所需工时分别为2h,1h.A、B两种设备每月有效使用台时数分别为400h和500h。如何安排生产可使收入最大?
解: 设每月生产甲产品x件,生产乙产品y件,每月收入为Z千元,目标函数为Z=3x+2y,满足的条件是
Z= 3x+2y 变形为
它表示斜率为 的直线系,Z与这条直线的截距有关。
X
Y
O
400
200
250
500
当直线经过点M时,截距最大,Z最大。
M
解方程组
可得M(200,100)
Z 的最大值Zmax =
3x+2y=800(千元)
故生产甲产品200件,
乙产品100件,收入最大,
为80万元。
1、不等式组 表示的平面区域内的整数点共有
( )个
能力提升:
1 2 3 4 x
3
2
1
0
4x+3y=12
2、设实数x、y满足约束条件:
则 的最大值为___________.
令k= ,则过点A(1, )时, kmax
第一课时
2x+y=0; 2x+y=1; 2x+y=-3; 2x+y=4; 2x+y=7
x
Y
o
斜率相同,截距不同的一族平行直线。
思考:
在同一坐标系中下列直线有什么异同点:
问题1:
某工厂用A,B两种配件生产甲,乙两种产品,
每生产一件甲种产品使用4个A配件耗时1h,
每生产一件乙种产品使用4个B配件耗时2h,
该厂每天最多可从配件厂获得16个A配件和
12个B配件,按每天工作8小时计算,该厂所有
可能的日生产安排是什么?
若生产1件甲种产品获利2万元,生产1 件乙
种产品获利3万元,采用哪种生产安排利润最大?
3
2
利润(万元)
8
2
1
所需时间
12
4
—
B种配件
16
—
4
A种配件
资源限额
乙产品
(1件)
甲产品
(1件)
产品
消 耗 量
资 源
把问题1的有关数据列表表示如下:
设甲,乙两种产品分别生产x, y件,
0
x
y
4
3
4
8
将上面不等式组表示成平面上的区域,区域内
所有坐标为整数的点P(x,y),安排生产任务x,y
都是有意义的.
设甲,乙两种产品分别生产x,y件,由己知条件可得:
问题:求利润2x+3y的最大值.
若设利润为z,则z=2x+3y,这样上述问题转化为:
当x,y在满足上述约束条件时,z的最大值为多少?
当点P在可允许的取值范围变化时,
0
x
y
4
3
4
8
M(4,2)
问题:求利润z=2x+3y的最大值.
象这样关于x,y一次不等
式组的约束条件称为
线性约束条件
Z=2x+3y称为目标函数,(因这里
目标函数为关于x,y的一次式,又
称为线性目标函数
在线性约束下求线性目标函数
的最值问题,统称为线性规划,
满足线性约束的解(x,y)叫做可行解,
所有可行解组成的集合叫做可行域
使目标函数取得最值的可行解叫做这个
问题的最优解
变式:若生产一件甲产品获利1万元,
生产一件乙产品获利3万元,采用哪种
生产安排利润最大?
0
x
y
4
3
4
8
N(2,3)
变式:求利润z=x+3y的最大值.
解线性规划问题的步骤:
(2)移:在线性目标函数所表示的一组平行线 中,利用平移的方法找出与可行域有公共点且
截距最大或最小的直线
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
P91:练习
1(1)求z=2x+y的最值,使式中的x、y满足约束条件:
x
O
y
A
B
C
y=x
x+y=1
y=-1
2x+y=0
B:(-1,-1)
C:(2,-1)
Z min=-3
Zmax=3
目标函数: Z=2x+y
小 结
本节主要学习了线性约束下如何求目
标函数的最值问题
正确列出变量的不等关系式,准确作出
可行域是解决目标函数最值的关健
线性目标函数的最值一般都是在可行域
的顶点或边界取得.
把目标函数转化为某一直线,其斜率与
可行域边界所在直线斜率的大小关系一定要
弄清楚.
3.3.2简单线性规划问题
第二课时
一、复习概念
把求最大值或求最小值的的函数称为目标函数,因为它是关于变量x、y的一次解析式,又称线性目标函数。
满足线性约束的解
(x,y)叫做可行解。
y
x
4
8
4
3
o
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
一组关于变量x、y的一次不等式,称为线性约束条件
由所有可行解组成的集合叫做可行域。
使目标函数取得最大值或最小值的可行解叫做这个问题的最优解。
可行域
可行解
最优解
二.回顾解线性规划问题的步骤
(2)移:在线性目标函数所表示的一组平行线 中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
P91:练习
1(1)求z=2x+y的最值,使式中的x、y满足约束条件:
x
O
y
A
B
C
y=x
x+y=1
y=-1
2x+y=0
B:(-1,-1)
C:(2,-1)
Z min=-3
Zmax=3
目标函数: Z=2x+y
例6、要将两种大小不同规格的钢板截成A、 B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 :
规格类型
钢板类型
第一种钢板
第二种钢板
A规格
B规格
C规格
2
1
2
1
3
1
今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。
解:设需截第一种钢板x张、第二种钢板y张,可得
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
2x+y≥15,
{
x+2y≥18,
x+3y≥27,
x≥0, x∈N*
y≥0 y∈N*
经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.
答:(略)
作出一组平行直线z= x+y,
目标函数z=x+y
B(3,9)
C(4,8)
A(18/5,39/5)
打网格线法
在可行域内打出网格线,
当直线经过点A时z=x+y=11.4,但它不是最优整数解,
将直线x+y=11.4继续向上平移,
2x+y=15
x+3y=27
x+2y=18
x+y =0
直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.
所以Z min=12
作出一组平行直线z = x+y,
目标函数
z = x+y
B(3,9)
C(4,8)
A(18/5,39/5)
当直线经过点A时z=x+y=11.4,但它不是最优整数解.
x+y=12
调整优值法
2x+y≥15,
{
x+2y≥18,
x+3y≥27,
x≥0, x∈N*
y≥0 y∈N*
x
0
y
在可行域内找出最优解、线性规划整数解问题的一般方法是:
1.若区域“顶点”处恰好为整点,那么它就是最优解;(在包括边界的情况下)
2.若区域“顶点”不是整点或不包括边界时,应先求出该点坐标,并计算目标函数值Z,然后在可行域内适当放缩目标函数值,使它为整数,且与Z最接近,在这条对应的直线中,取可行域内整点,如果没有整点,继续放缩,直至取到整点为止。 (调整优值法)
3.在可行域内找整数解,一般采用平移找解法,即打网络、找整点、平移直线、找出整数最优解
例7:一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t、硝酸盐18t;生产1车皮乙种肥料需要的主要原料是磷酸盐1t、硝酸盐15t。现库存磷酸盐10t、硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域。并计算生产甲、乙两种肥料各多少车皮,能够产生最大的利润?
解:设x、y分别为计划生产甲、乙两种混合
肥料的车皮数,于是满足以下条件:
x
y
o
解:设生产甲种肥料x车皮、乙种肥料y车皮,能够产生利润Z万元。目标函数为Z=x+0.5y,可行域如图:
把Z=x+0.5y变形为y=-2x+2z,它表示斜率为-2,在y轴上的截距为2z的一组直线系。
x
y
o
由图可以看出,当直线经过可行域上的点M时,
截距2z最大,即z最大。
答:生产甲种、乙种肥料各2车皮,能够产生最大利润,最大利润为3万元。
M
容易求得M点的坐标为(2,2),则Zmax=3
作业布置
课本 P91 :
第1(2)、2题
小 结:
二元一次不等式
表示平面区域
直线定界,
特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:画、移、求、答
P91 练习 2
某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元、2000元,甲、乙产品都需要在A、B两种设备上加工,在每台A、B上加工1件甲所需工时分别为1h、2h,加工1件乙所需工时分别为2h,1h.A、B两种设备每月有效使用台时数分别为400h和500h。如何安排生产可使收入最大?
解: 设每月生产甲产品x件,生产乙产品y件,每月收入为Z千元,目标函数为Z=3x+2y,满足的条件是
Z= 3x+2y 变形为
它表示斜率为 的直线系,Z与这条直线的截距有关。
X
Y
O
400
200
250
500
当直线经过点M时,截距最大,Z最大。
M
解方程组
可得M(200,100)
Z 的最大值Zmax =
3x+2y=800(千元)
故生产甲产品200件,
乙产品100件,收入最大,
为80万元。
1、不等式组 表示的平面区域内的整数点共有
( )个
能力提升:
1 2 3 4 x
3
2
1
0
4x+3y=12
2、设实数x、y满足约束条件:
则 的最大值为___________.
令k= ,则过点A(1, )时, kmax
