高中数学人教A版选修2-1第二章2.3.1双曲线及其标准方程课件(15张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-1第二章2.3.1双曲线及其标准方程课件(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 501.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览



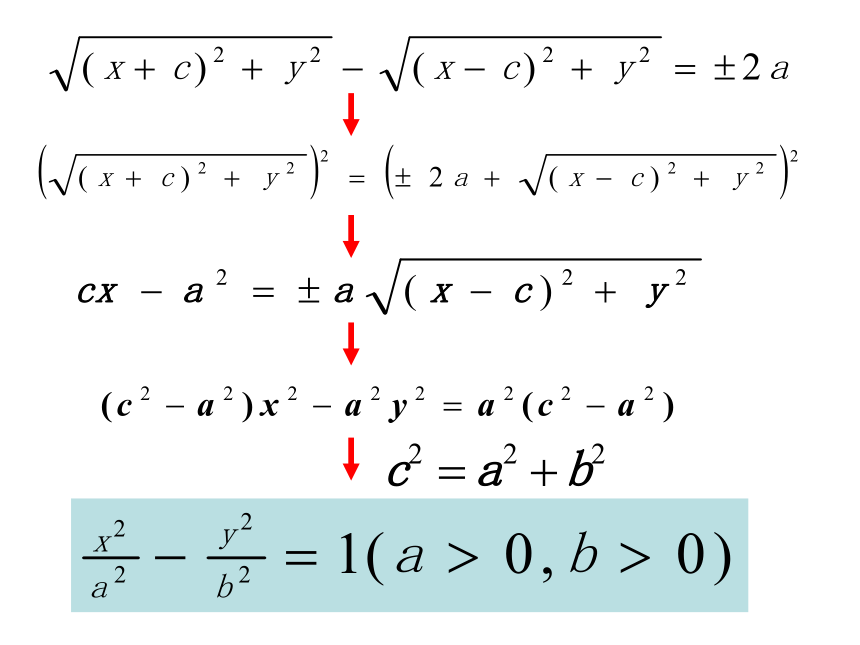
文档简介
2.3.1 双曲线及其标准方程
椭圆的定义:平面内与两定点F1,F2的距离的和等于常数(大于 F1F2 )的点的轨迹叫做椭圆。
思考:平面内与两定点F1,F2的距离的差为非零常数的点的轨迹是什么?
复习引入
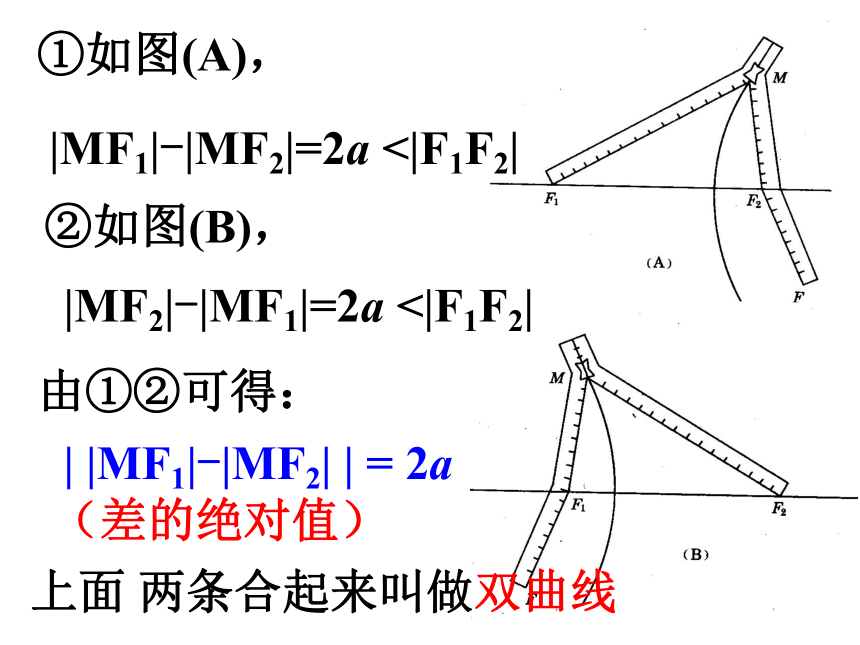
①如图(A),
|MF1|-|MF2|=2a <|F1F2|
②如图(B),
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
|MF2|-|MF1|=2a <|F1F2|
o
F
2
F
1
M
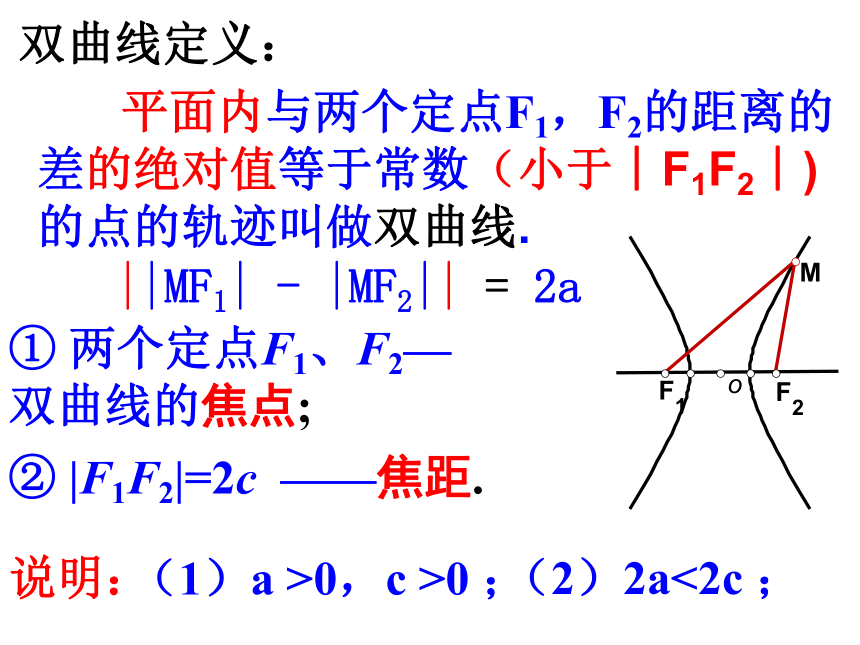
① 两个定点F1、F2—
双曲线的焦点;
② |F1F2|=2c ——焦距.
(2)2a<2c ;
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
(1)a >0,c >0 ;
双曲线定义:
说明:
||MF1| - |MF2|| = 2a
注意:
(2)若2a=2c,则轨迹是什么?
(3)若2a>2c,则轨迹是什么?
(4)若2a=0,则轨迹是什么?
F1F2延长线和反向延长线(两条射线)
轨迹不存在
线段F1F2的垂直平分线
(1)当|MF1|-|MF2|=2a时,点M的轨迹
为近F2的一支(右支)
当|MF1|-|MF2|=-2a时,点M的轨迹
为近F1的一支(左支)
练习:
P61A组第1题
y
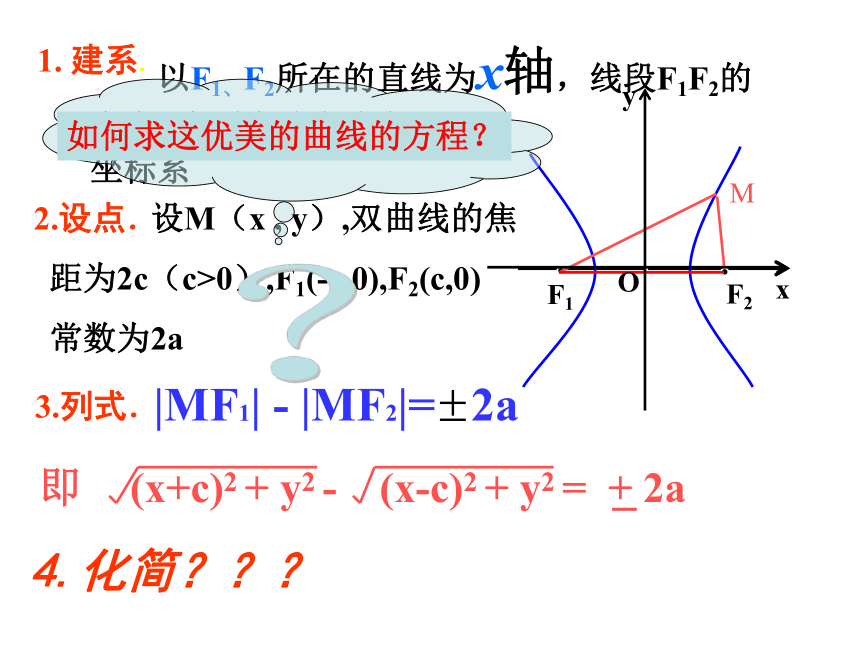
设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数为2a
M
即 (x+c)2 + y2 - (x-c)2 + y2 = + 2a
_
以F1、F2所在的直线为x轴,线段F1F2的中点o为原点建立直角
坐标系
1. 建系.
2.设点.
3.列式.
|MF1| - |MF2|= 2a
如何求这优美的曲线的方程?
?
4.化简???
F1
F2
x
O
y
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
若建系时,焦点在y轴上呢?
焦点在x轴的标准方程
焦点在y轴上的标准方程
如何判断双曲线的焦点在哪个轴上?
看x2与y2的系数符号,当x2,y2哪个系数为正,焦点就在哪个轴上,双曲线的焦点所在位置与分母的大小无关。
解:因为双曲线的焦点位置不确定,所以设双曲线方程为mx2+ny2=1(mn<0),∵P1、P2在双曲线上,所以有
方法:“巧设”方程为“ ”
避免分两种情况进行讨论。
例1, 已知双曲线的两个焦点坐标为F1(-5,0)、F2(5,0)双曲线上一 点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程。
例2:一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处晚2 s.
(1)爆炸点应在什么样的曲线上?
(2)已知A、B两地相距800 m,并且此时声速为340 m/s,求曲线的方程.
P
O
x
B
A
y
练习:
P55 第2,3题
作业布置:
P55 练习 第1题
P61 A组 第2题
双曲线
定义
图形
标准方程
焦点坐标
关系
( 为定点, 为常数)
小结
| |MF1|-|MF2| | =2a
练习巩固:
已知定点A(3,0)和定圆C:(x+3)2+y2=16,动圆与圆C相切, 并过点A,求动圆圆心P的轨迹方程.
解:设动圆圆心为P(x,y),由已知条件得,圆C的圆心为B(-3,0) ,则有|PBl-IPAl=4,符合双曲线的定义.
椭圆的定义:平面内与两定点F1,F2的距离的和等于常数(大于 F1F2 )的点的轨迹叫做椭圆。
思考:平面内与两定点F1,F2的距离的差为非零常数的点的轨迹是什么?
复习引入
①如图(A),
|MF1|-|MF2|=2a <|F1F2|
②如图(B),
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
|MF2|-|MF1|=2a <|F1F2|
o
F
2
F
1
M
① 两个定点F1、F2—
双曲线的焦点;
② |F1F2|=2c ——焦距.
(2)2a<2c ;
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
(1)a >0,c >0 ;
双曲线定义:
说明:
||MF1| - |MF2|| = 2a
注意:
(2)若2a=2c,则轨迹是什么?
(3)若2a>2c,则轨迹是什么?
(4)若2a=0,则轨迹是什么?
F1F2延长线和反向延长线(两条射线)
轨迹不存在
线段F1F2的垂直平分线
(1)当|MF1|-|MF2|=2a时,点M的轨迹
为近F2的一支(右支)
当|MF1|-|MF2|=-2a时,点M的轨迹
为近F1的一支(左支)
练习:
P61A组第1题
y
设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数为2a
M
即 (x+c)2 + y2 - (x-c)2 + y2 = + 2a
_
以F1、F2所在的直线为x轴,线段F1F2的中点o为原点建立直角
坐标系
1. 建系.
2.设点.
3.列式.
|MF1| - |MF2|= 2a
如何求这优美的曲线的方程?
?
4.化简???
F1
F2
x
O
y
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
若建系时,焦点在y轴上呢?
焦点在x轴的标准方程
焦点在y轴上的标准方程
如何判断双曲线的焦点在哪个轴上?
看x2与y2的系数符号,当x2,y2哪个系数为正,焦点就在哪个轴上,双曲线的焦点所在位置与分母的大小无关。
解:因为双曲线的焦点位置不确定,所以设双曲线方程为mx2+ny2=1(mn<0),∵P1、P2在双曲线上,所以有
方法:“巧设”方程为“ ”
避免分两种情况进行讨论。
例1, 已知双曲线的两个焦点坐标为F1(-5,0)、F2(5,0)双曲线上一 点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程。
例2:一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处晚2 s.
(1)爆炸点应在什么样的曲线上?
(2)已知A、B两地相距800 m,并且此时声速为340 m/s,求曲线的方程.
P
O
x
B
A
y
练习:
P55 第2,3题
作业布置:
P55 练习 第1题
P61 A组 第2题
双曲线
定义
图形
标准方程
焦点坐标
关系
( 为定点, 为常数)
小结
| |MF1|-|MF2| | =2a
练习巩固:
已知定点A(3,0)和定圆C:(x+3)2+y2=16,动圆与圆C相切, 并过点A,求动圆圆心P的轨迹方程.
解:设动圆圆心为P(x,y),由已知条件得,圆C的圆心为B(-3,0) ,则有|PBl-IPAl=4,符合双曲线的定义.
