高中数学人教A版选修2-1第二章2.3.2双曲线的简单几何性质课件(21张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-1第二章2.3.2双曲线的简单几何性质课件(21张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览






文档简介
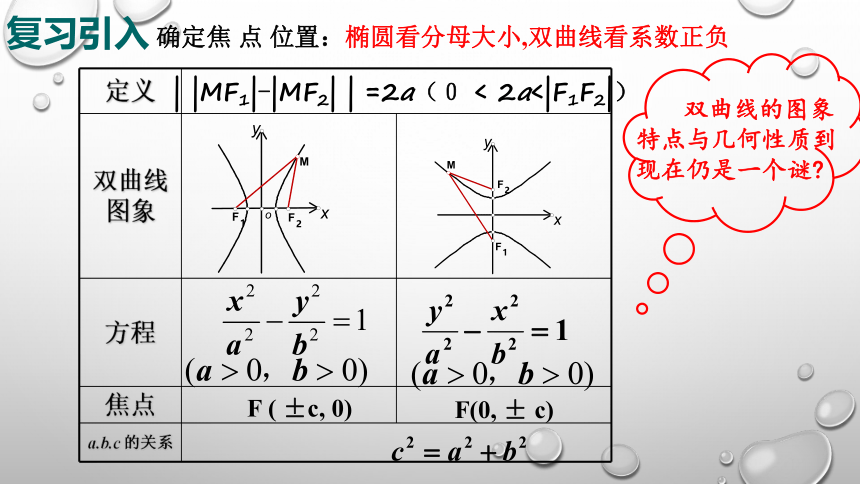
定义
双曲线图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0)
确定焦 点 位置:椭圆看分母大小,双曲线看系数正负
F(0, ± c)
双曲线的图象特点与几何性质到现在仍是一个谜?
复习引入
复习引入
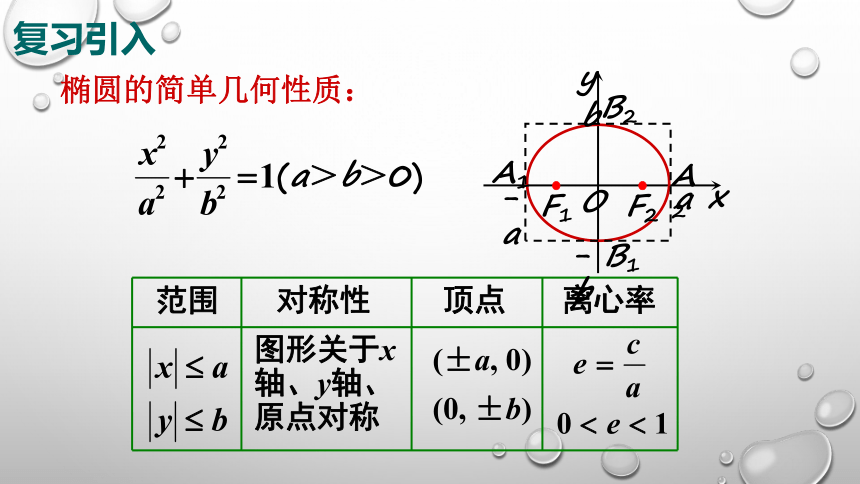
(±a, 0)
(0, ±b)
图形关于x
轴、y轴、
原点对称
范围
对称性
顶点
离心率
(a>b>0)
椭圆的简单几何性质:
y
O
F1
F2
x
B2
B1
A1
A2
-a
a
b
-b
双曲线的简单几何性质
制作人:谷聪敏
日 期:2010.10
1.熟悉双曲线的几何性质:对称性、范围、顶点、渐近线、离心率
2.能说明离心率的大小对双曲线形状的影响.
学习目标
一、焦点在x轴上的双曲线的几何性质
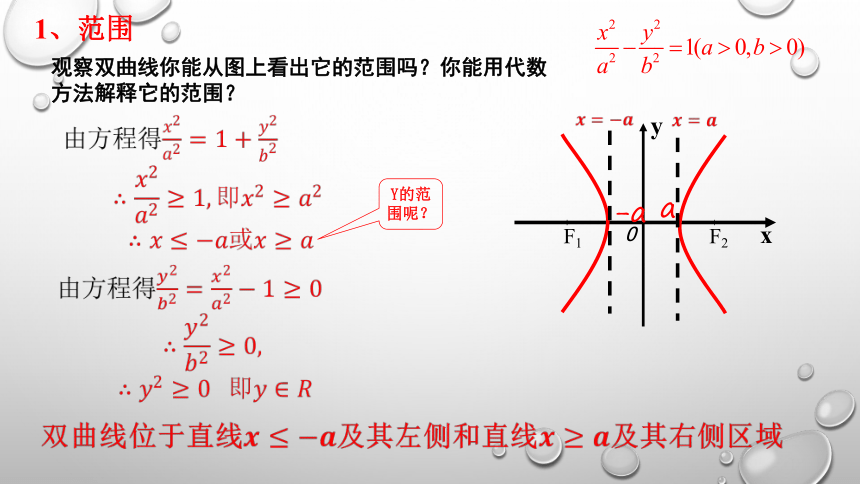
观察双曲线你能从图上看出它的范围吗?你能用代数方法解释它的范围?
y
F1
O
F2
x
1、范围
Y的范围呢?
?
?
-a
a
?
?
?
x
y
o
(-x,-y)
(-x,y)
(x,y))
(x,-y)
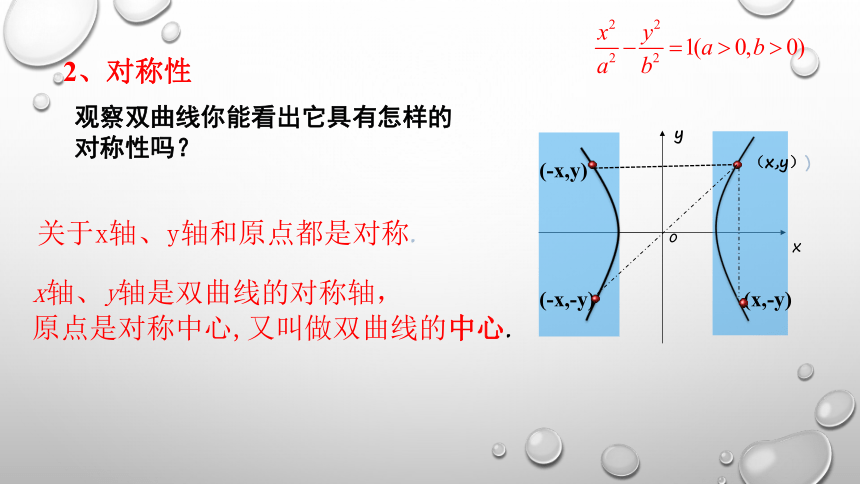
关于x轴、y轴和原点都是对称.
x轴、y轴是双曲线的对称轴,
原点是对称中心,又叫做双曲线的中心.
2、对称性
观察双曲线你能看出它具有怎样的对称性吗?
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
(3)实轴与虚轴等长的双曲线叫等轴双曲线。
观察双曲线你能发现哪些点比较特殊?
?
?
4、渐近线
x
y
o
a
b
可以看出,双曲线
的各支向外延伸时,与直线
逐渐接近,我们把这两条直线
叫做双曲线的渐近线。
双曲线与渐近线无限接近,但永不相交。
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
Y
X
F1
F2
A1
A2
B1
B2
焦点在x轴上的双曲线草图画法
5、离心率
离心率。
c>a>0
e >1
e是表示双曲线开口大小的一个量
e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
x
y
o
b
a
等轴双曲线方程为x2-y2=m,渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.
思考:等轴双曲线性质?
(5)渐近线方程:
随堂练习1
二、焦点在y轴上的双曲线的几何性质
焦点在y轴上的双曲线的几何性质
双曲线标准方程:
双曲线性质:
1.范围:
2.对称性:
3.顶点:
4.渐近线方程:
5.离心率:
y≥a或y≤-a
关于坐标轴和原点对称
A1(0,-a),A2(0,a)
A1A2为实轴,B1B2为虚轴
类比焦点在x轴上的双曲线的性质,给出焦点在y轴上的双曲线的几何性质。
求双曲线 9y2-16x2=144的实半轴和虚半轴长、
焦点坐标、离心率.
随堂练习2
小结
一个特例:
五个性质:
一、三、五
等轴双曲线
三个意识:
类比意识、数形结合意识、发现意识
范围、顶点、对称性、离心率、渐近线
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
当堂检测
双曲线图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0)
确定焦 点 位置:椭圆看分母大小,双曲线看系数正负
F(0, ± c)
双曲线的图象特点与几何性质到现在仍是一个谜?
复习引入
复习引入
(±a, 0)
(0, ±b)
图形关于x
轴、y轴、
原点对称
范围
对称性
顶点
离心率
(a>b>0)
椭圆的简单几何性质:
y
O
F1
F2
x
B2
B1
A1
A2
-a
a
b
-b
双曲线的简单几何性质
制作人:谷聪敏
日 期:2010.10
1.熟悉双曲线的几何性质:对称性、范围、顶点、渐近线、离心率
2.能说明离心率的大小对双曲线形状的影响.
学习目标
一、焦点在x轴上的双曲线的几何性质
观察双曲线你能从图上看出它的范围吗?你能用代数方法解释它的范围?
y
F1
O
F2
x
1、范围
Y的范围呢?
?
?
-a
a
?
?
?
x
y
o
(-x,-y)
(-x,y)
(x,y))
(x,-y)
关于x轴、y轴和原点都是对称.
x轴、y轴是双曲线的对称轴,
原点是对称中心,又叫做双曲线的中心.
2、对称性
观察双曲线你能看出它具有怎样的对称性吗?
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
(3)实轴与虚轴等长的双曲线叫等轴双曲线。
观察双曲线你能发现哪些点比较特殊?
?
?
4、渐近线
x
y
o
a
b
可以看出,双曲线
的各支向外延伸时,与直线
逐渐接近,我们把这两条直线
叫做双曲线的渐近线。
双曲线与渐近线无限接近,但永不相交。
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
Y
X
F1
F2
A1
A2
B1
B2
焦点在x轴上的双曲线草图画法
5、离心率
离心率。
c>a>0
e >1
e是表示双曲线开口大小的一个量
e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
x
y
o
b
a
等轴双曲线方程为x2-y2=m,渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.
思考:等轴双曲线性质?
(5)渐近线方程:
随堂练习1
二、焦点在y轴上的双曲线的几何性质
焦点在y轴上的双曲线的几何性质
双曲线标准方程:
双曲线性质:
1.范围:
2.对称性:
3.顶点:
4.渐近线方程:
5.离心率:
y≥a或y≤-a
关于坐标轴和原点对称
A1(0,-a),A2(0,a)
A1A2为实轴,B1B2为虚轴
类比焦点在x轴上的双曲线的性质,给出焦点在y轴上的双曲线的几何性质。
求双曲线 9y2-16x2=144的实半轴和虚半轴长、
焦点坐标、离心率.
随堂练习2
小结
一个特例:
五个性质:
一、三、五
等轴双曲线
三个意识:
类比意识、数形结合意识、发现意识
范围、顶点、对称性、离心率、渐近线
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
当堂检测
