高中数学人教A版选修2-2第一章1.3.2函数的极值与导数 课件(17张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-2第一章1.3.2函数的极值与导数 课件(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 456.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 16:04:34 | ||
图片预览



文档简介
1.3.2函数的极值与导数
高二数学 选修 2-2 1.3导数在研究函数中的应用
一、复习导入
解
区间
(-∞,-4)
-4
(-4,2)
2
(2,+∞)
f '(x)
0
0
f(x)
f(x)在(-∞,-4)、 (2,+∞)内单调递增,
临界点处
函数值有什么特点?
+
+
-
f ’(x)>0 (x+4)(x-2)>0 x<-4或x>2
f(x)在(-4,2)内单调递减。
f ’(x)<0 (x+4)(x-2)<0 -4一、复习导入
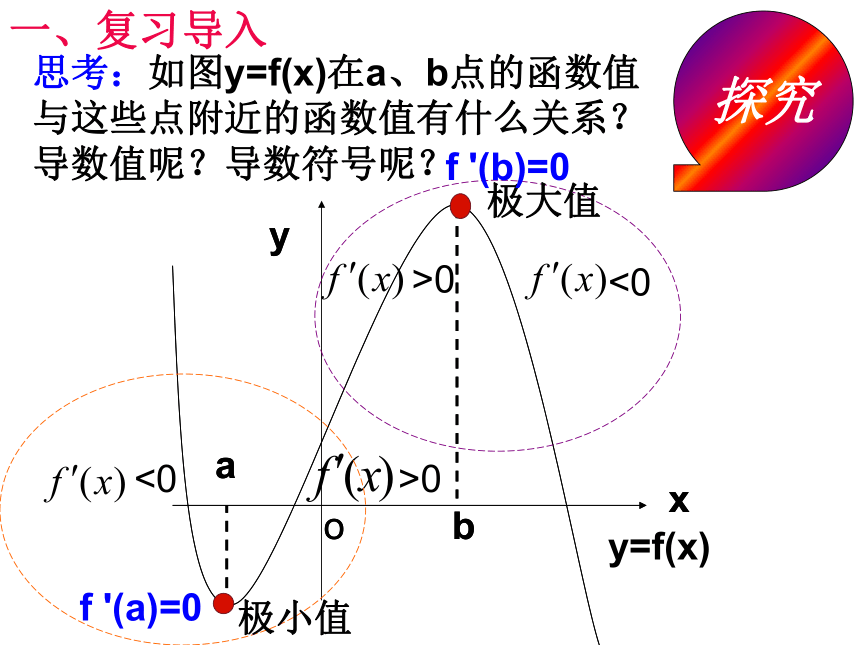
思考:如图y=f(x)在a、b点的函数值
与这些点附近的函数值有什么关系?
导数值呢?导数符号呢?
探究
x
y
o
a
b
x
y
o
a
b
y=f(x)
>0
<0
<0
>0
极小值
极大值
f '(a)=0
f '(b)=0
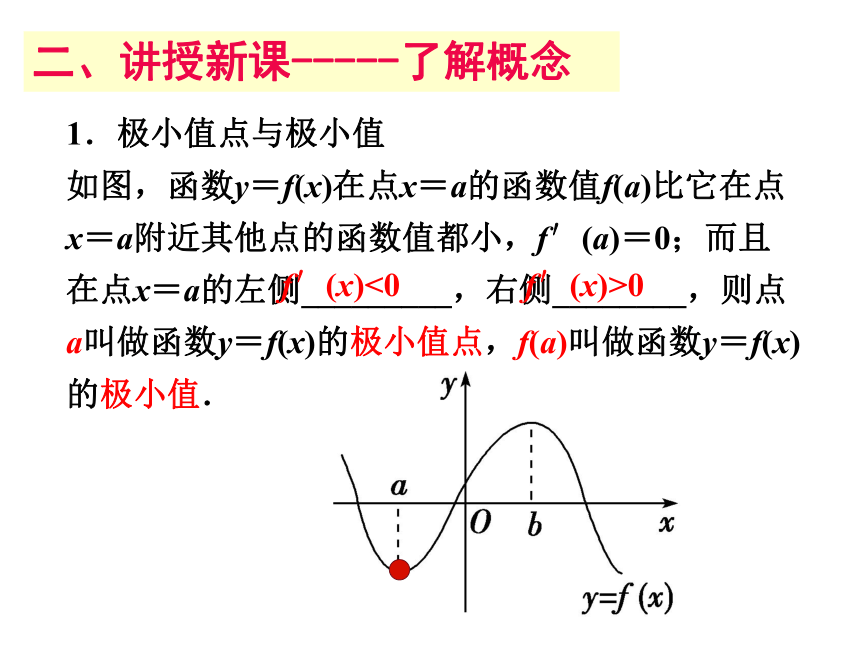
1.极小值点与极小值
如图,函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a的左侧_________,右侧________,则点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
f′(x)<0
f′(x)>0
二、讲授新课-----了解概念
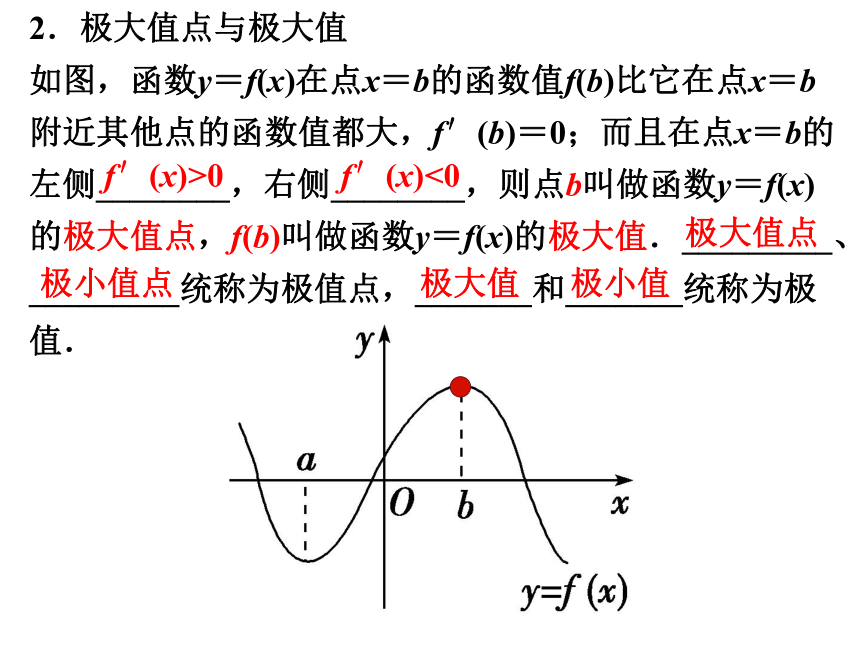
2.极大值点与极大值
如图,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b的左侧________,右侧________,则点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值._________、_________统称为极值点,_______和_______统称为极值.
f′(x)>0
f′(x)<0
极大值点
极小值点
极大值
极小值
f ?(x)<0
y
x
O
x1
a
b
y=f(x)
极大值点两侧
极小值点两侧
f ?(x)<0
f ?(x)>0
f ?(x)>0
x2
x
x x2
x>x2
f?(x)
f(x)
x
x x1
x>x1
f?(x)
f(x)
增
f?(x) >0
f?(x) =0
f?(x) <0
极大值
减
f?(x) <0
f?(x) =0
增
减
极小值
f?(x) >0
结论:极值点处,f?(x) =0
思考:极值点两侧函数图象单调性有何特点?
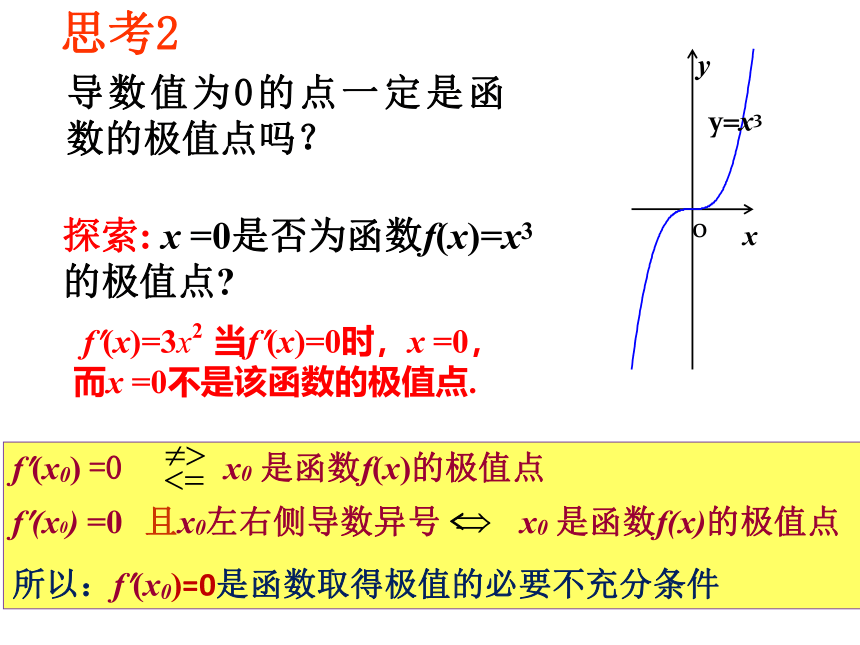
导数值为0的点一定是函数的极值点吗?
思考2
探索: x =0是否为函数f(x)=x3
的极值点?
x
y
o
y?x3
f?(x)=3x2 当f?(x)=0时,x =0,
而x =0不是该函数的极值点.
f?(x0) =0 x0 是函数f(x)的极值点
f?(x0) =0 且x0左右侧导数异号﹤ x0 是函数f(x)的极值点
所以:f?(x0)=0是函数取得极值的必要不充分条件
思考
极大值一定比极小值大吗?
极值是函数的局部性概念
结论:不一定
极大值
极小值
极小值
练习1
下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.
a
b
x
y
x1
O
x2
x3
x4
x5
x6
因为 所以
例1 求函数 的极值.
解:
令 解得 或
当 , 即 , 或 ;
当 , 即 .
当 x 变化时, f?(x)、f (x) 的变化情况如下表:
x
(–∞, –2)
–2
(–2, 2)
2
( 2, +∞)
0
0
f (x)
28 / 3
– 4 / 3
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –2 时, f (x)有极大值, 并且为f (-2)= 28 / 3 ;
当 x = 2 时, f (x)有极小值, 并且为 f (2)= – 4 / 3 .
例1的图象:
-2
o
x
y
2
28/3
-4/3
求函数极值(极大值,极小值)的一般步骤:
(1)确定函数的定义域
(2)求方程f'(x)=0的根
(3)用方程f'(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f'(x)在方程f'(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
若f'(x0)左正右负,则f(x0)为极大值;
若f‘(x0)左负右正,则f(x0)为极小值。
+
-
x0
-
+
x0
定义域—求导—求根—列表—求极值
练习2
必要条件
函数极值与导数
函数极值的定义
函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.
函数极值的求法
求极值的步骤:1.定义域, 2 .求导 ,3 .令y’=0 , 4.列表 , 5.求极值
小结:
练习1
求下列函数的极值:
解:
令 解得 列表:
x
0
f (x)
+
单调递增
单调递减
–
所以, 当 时, f (x)有极小值
练习2
求下列函数的极值:
解:
解得 列表:
x
(–∞, –3)
–3
(–3, 3)
3
( 3, +∞)
0
0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –3 时, f (x)有极大值 54 ;
当 x = 3 时, f (x)有极小值 – 54 .
高二数学 选修 2-2 1.3导数在研究函数中的应用
一、复习导入
解
区间
(-∞,-4)
-4
(-4,2)
2
(2,+∞)
f '(x)
0
0
f(x)
f(x)在(-∞,-4)、 (2,+∞)内单调递增,
临界点处
函数值有什么特点?
+
+
-
f ’(x)>0 (x+4)(x-2)>0 x<-4或x>2
f(x)在(-4,2)内单调递减。
f ’(x)<0 (x+4)(x-2)<0 -4
思考:如图y=f(x)在a、b点的函数值
与这些点附近的函数值有什么关系?
导数值呢?导数符号呢?
探究
x
y
o
a
b
x
y
o
a
b
y=f(x)
>0
<0
<0
>0
极小值
极大值
f '(a)=0
f '(b)=0
1.极小值点与极小值
如图,函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a的左侧_________,右侧________,则点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
f′(x)<0
f′(x)>0
二、讲授新课-----了解概念
2.极大值点与极大值
如图,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b的左侧________,右侧________,则点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值._________、_________统称为极值点,_______和_______统称为极值.
f′(x)>0
f′(x)<0
极大值点
极小值点
极大值
极小值
f ?(x)<0
y
x
O
x1
a
b
y=f(x)
极大值点两侧
极小值点两侧
f ?(x)<0
f ?(x)>0
f ?(x)>0
x2
x
x
x>x2
f?(x)
f(x)
x
x
x>x1
f?(x)
f(x)
增
f?(x) >0
f?(x) =0
f?(x) <0
极大值
减
f?(x) <0
f?(x) =0
增
减
极小值
f?(x) >0
结论:极值点处,f?(x) =0
思考:极值点两侧函数图象单调性有何特点?
导数值为0的点一定是函数的极值点吗?
思考2
探索: x =0是否为函数f(x)=x3
的极值点?
x
y
o
y?x3
f?(x)=3x2 当f?(x)=0时,x =0,
而x =0不是该函数的极值点.
f?(x0) =0 x0 是函数f(x)的极值点
f?(x0) =0 且x0左右侧导数异号﹤ x0 是函数f(x)的极值点
所以:f?(x0)=0是函数取得极值的必要不充分条件
思考
极大值一定比极小值大吗?
极值是函数的局部性概念
结论:不一定
极大值
极小值
极小值
练习1
下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.
a
b
x
y
x1
O
x2
x3
x4
x5
x6
因为 所以
例1 求函数 的极值.
解:
令 解得 或
当 , 即 , 或 ;
当 , 即 .
当 x 变化时, f?(x)、f (x) 的变化情况如下表:
x
(–∞, –2)
–2
(–2, 2)
2
( 2, +∞)
0
0
f (x)
28 / 3
– 4 / 3
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –2 时, f (x)有极大值, 并且为f (-2)= 28 / 3 ;
当 x = 2 时, f (x)有极小值, 并且为 f (2)= – 4 / 3 .
例1的图象:
-2
o
x
y
2
28/3
-4/3
求函数极值(极大值,极小值)的一般步骤:
(1)确定函数的定义域
(2)求方程f'(x)=0的根
(3)用方程f'(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f'(x)在方程f'(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
若f'(x0)左正右负,则f(x0)为极大值;
若f‘(x0)左负右正,则f(x0)为极小值。
+
-
x0
-
+
x0
定义域—求导—求根—列表—求极值
练习2
必要条件
函数极值与导数
函数极值的定义
函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.
函数极值的求法
求极值的步骤:1.定义域, 2 .求导 ,3 .令y’=0 , 4.列表 , 5.求极值
小结:
练习1
求下列函数的极值:
解:
令 解得 列表:
x
0
f (x)
+
单调递增
单调递减
–
所以, 当 时, f (x)有极小值
练习2
求下列函数的极值:
解:
解得 列表:
x
(–∞, –3)
–3
(–3, 3)
3
( 3, +∞)
0
0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –3 时, f (x)有极大值 54 ;
当 x = 3 时, f (x)有极小值 – 54 .
