高中数学人教A版选修2-3第二章:2.3.1_离散型随机变量的均值 课件(23张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-3第二章:2.3.1_离散型随机变量的均值 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 489.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 16:50:19 | ||
图片预览








文档简介
2.3.1离散型随机变量的均值
复习
什么叫做n次独立重复实验?
设X表示n次实验中A事件发生的次数,它满足什么分布?分布列如何表示?
如果X满足二项分布,则
记为:X~B (n,p)
如果你期中考试各门成绩为:
90、80、77、68、85、91
那你的平均成绩是多少?
算术平均数
加权平均数
你的期中数学考试成绩为70,平时表现成绩为60,学校规定:在你学分记录表中,该学期的数学成绩中考试成绩占70%、平时成绩占30%,你最终的数学成绩为多少?
加权平均数
权:称棰,权衡轻重的数值;
加权平均:计算若干数量的平均数时,考虑到每个数量在总量中所具有的重要性不同,分别给予不同的权数。
思考
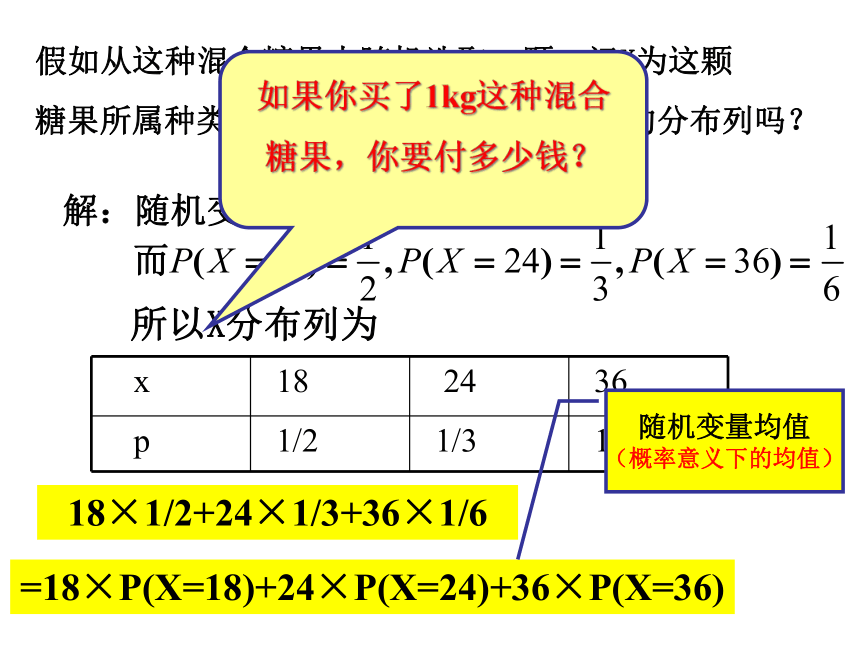
某商场要将单价分别为18元/kg、24元/kg、36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?
定价为
可以吗?
18×1/2+24×1/3+36×1/6
x
18
24
36
p
1/2
1/3
1/6
=18×P(X=18)+24×P(X=24)+36×P(X=36)
如果你买了1kg这种混合
糖果,你要付多少钱?
随机变量均值(概率意义下的均值)
离散型随机变量取值的平均值:
数学期望
一般地,若离散型随机变量X的概率分布为:
则称
为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。
···
···
···
···
?
随机变量的均值与样本的平均值有何区别和联系
随机变量的均值是常数,而样本的平均值随
着样本的不同而变化,因而样本的平均值是
随机变量;
对于简单随机样本,随着样本容量的增加,
样本的平均值越来越接近总体的平均值,因
此,我们常用样本的平均值来估计总体的平
均值。
例:
随机抛掷一个均匀的骰子,求所得骰子的点数X的期望.
X
1
2
3
4
5
6
P
1/6
1/6
1/6
1/6
1/6
1/6
解:随机变量X的取值为1,2,3,4,5,6
其分布列为
所以随机变量X的均值为E(X)=1× 1/6+2× 1/6
+3×1/6+4× 1/6+5× 1/6+6× 1/6=3.5
Y
3
5
7
9
11
13
P
1/6
1/6
1/6
1/6
1/6
1/6
解:随机变量X的取值为1,2,3,4,5,6
其分布列为
所以随机变量Y的均值为 E(Y) =3× 1/6+5× 1/6
+7×1/6+9× 1/6+11× 1/6+13× 1/6=8
=2E(X)+1
变式:将所得点数的2倍加1作为得分数, 即Y=2X+1,试求Y的期望?
离散型随机变量均值的线性性质
例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?
一般地,如果随机变量X服从两点分布,
X
1
0
P
p
1-p
则
例题讲解
小结:
例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。
X
0
1
2
3
P
解:
(1) X~B(3,0.7)
(2)
1、均值的线性性质
2、两种特殊分布的均值
(1)若随机变量X服从两点分布,则
(2)若 ,则
小结:离散型随机变量均值的性质
3、求离散型随机变量均值的步骤:
①确定所有可能取值;②写出分布列;
③求出均值
例:一次单元测验由20个选择题构成,每个选择题有4个选项,其中有且只有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分,学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和乙在这次英语单元测验中的成绩的期望。
不一定,其含义是在多次类似的测试中,他的平均成绩大约是90分
思考:学生甲在这次测试中的成绩一定会是90分吗?他的均值为90分的含义是什么?
例:根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元。为保护设备,有以下种方案:
方案1:运走设备,搬运费为3800元。
方案2:建保护围墙,建设费为2000元,但围墙只能挡住小洪水。
方案3:不采取措施,希望不发生洪水。
试比较哪一种方案好。
自主学习
小 结
1. 离散型随机变量均值的性质
若X~B(n,p), 则E(X)= np
若X~B(1,p), 则E(X)= p
2. 求离散型随机变量均值的步骤
①确定所有可能取值;②写出分布列;③求出均值
做练习:
P64 第2—5题
P68 A组:第2,3,4题
作业布置:
1、完成好《全优课堂》
2、预习新课2.3.2
提升练习1:
已知随机变量X的分布列如下:
某学校要从5名男生和2名女生中选出2人作为上海世博会
志愿者,若用随机变量ξ表示选出的志愿者中女生的人
数,则数学期望 E(ξ)=______(结果用最简分数表示).
解:ξ的可能取值为0,1,2,
提升练习2:
复习
什么叫做n次独立重复实验?
设X表示n次实验中A事件发生的次数,它满足什么分布?分布列如何表示?
如果X满足二项分布,则
记为:X~B (n,p)
如果你期中考试各门成绩为:
90、80、77、68、85、91
那你的平均成绩是多少?
算术平均数
加权平均数
你的期中数学考试成绩为70,平时表现成绩为60,学校规定:在你学分记录表中,该学期的数学成绩中考试成绩占70%、平时成绩占30%,你最终的数学成绩为多少?
加权平均数
权:称棰,权衡轻重的数值;
加权平均:计算若干数量的平均数时,考虑到每个数量在总量中所具有的重要性不同,分别给予不同的权数。
思考
某商场要将单价分别为18元/kg、24元/kg、36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?
定价为
可以吗?
18×1/2+24×1/3+36×1/6
x
18
24
36
p
1/2
1/3
1/6
=18×P(X=18)+24×P(X=24)+36×P(X=36)
如果你买了1kg这种混合
糖果,你要付多少钱?
随机变量均值(概率意义下的均值)
离散型随机变量取值的平均值:
数学期望
一般地,若离散型随机变量X的概率分布为:
则称
为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。
···
···
···
···
?
随机变量的均值与样本的平均值有何区别和联系
随机变量的均值是常数,而样本的平均值随
着样本的不同而变化,因而样本的平均值是
随机变量;
对于简单随机样本,随着样本容量的增加,
样本的平均值越来越接近总体的平均值,因
此,我们常用样本的平均值来估计总体的平
均值。
例:
随机抛掷一个均匀的骰子,求所得骰子的点数X的期望.
X
1
2
3
4
5
6
P
1/6
1/6
1/6
1/6
1/6
1/6
解:随机变量X的取值为1,2,3,4,5,6
其分布列为
所以随机变量X的均值为E(X)=1× 1/6+2× 1/6
+3×1/6+4× 1/6+5× 1/6+6× 1/6=3.5
Y
3
5
7
9
11
13
P
1/6
1/6
1/6
1/6
1/6
1/6
解:随机变量X的取值为1,2,3,4,5,6
其分布列为
所以随机变量Y的均值为 E(Y) =3× 1/6+5× 1/6
+7×1/6+9× 1/6+11× 1/6+13× 1/6=8
=2E(X)+1
变式:将所得点数的2倍加1作为得分数, 即Y=2X+1,试求Y的期望?
离散型随机变量均值的线性性质
例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?
一般地,如果随机变量X服从两点分布,
X
1
0
P
p
1-p
则
例题讲解
小结:
例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。
X
0
1
2
3
P
解:
(1) X~B(3,0.7)
(2)
1、均值的线性性质
2、两种特殊分布的均值
(1)若随机变量X服从两点分布,则
(2)若 ,则
小结:离散型随机变量均值的性质
3、求离散型随机变量均值的步骤:
①确定所有可能取值;②写出分布列;
③求出均值
例:一次单元测验由20个选择题构成,每个选择题有4个选项,其中有且只有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分,学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和乙在这次英语单元测验中的成绩的期望。
不一定,其含义是在多次类似的测试中,他的平均成绩大约是90分
思考:学生甲在这次测试中的成绩一定会是90分吗?他的均值为90分的含义是什么?
例:根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元。为保护设备,有以下种方案:
方案1:运走设备,搬运费为3800元。
方案2:建保护围墙,建设费为2000元,但围墙只能挡住小洪水。
方案3:不采取措施,希望不发生洪水。
试比较哪一种方案好。
自主学习
小 结
1. 离散型随机变量均值的性质
若X~B(n,p), 则E(X)= np
若X~B(1,p), 则E(X)= p
2. 求离散型随机变量均值的步骤
①确定所有可能取值;②写出分布列;③求出均值
做练习:
P64 第2—5题
P68 A组:第2,3,4题
作业布置:
1、完成好《全优课堂》
2、预习新课2.3.2
提升练习1:
已知随机变量X的分布列如下:
某学校要从5名男生和2名女生中选出2人作为上海世博会
志愿者,若用随机变量ξ表示选出的志愿者中女生的人
数,则数学期望 E(ξ)=______(结果用最简分数表示).
解:ξ的可能取值为0,1,2,
提升练习2:
