高中数学人教A版选修2-3第二章:2.4正态分布 课件(19张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-3第二章:2.4正态分布 课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览




文档简介
2.4 正态分布
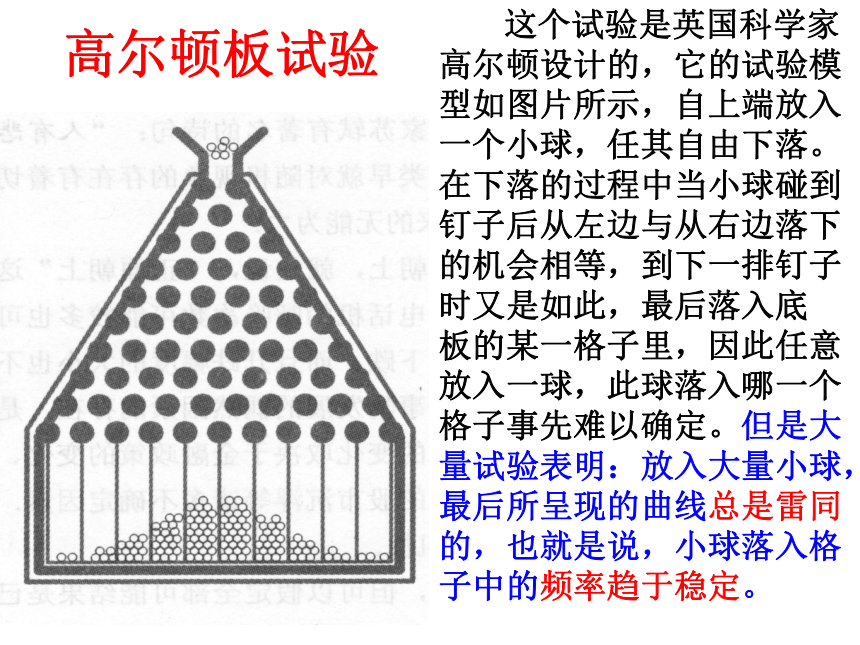
高尔顿板试验
这个试验是英国科学家高尔顿设计的,它的试验模型如图片所示,自上端放入一个小球,任其自由下落。在下落的过程中当小球碰到钉子后从左边与从右边落下的机会相等,到下一排钉子时又是如此,最后落入底
板的某一格子里,因此任意放入一球,此球落入哪一个格子事先难以确定。但是大量试验表明:放入大量小球,最后所呈现的曲线总是雷同的,也就是说,小球落入格子中的频率趋于稳定。
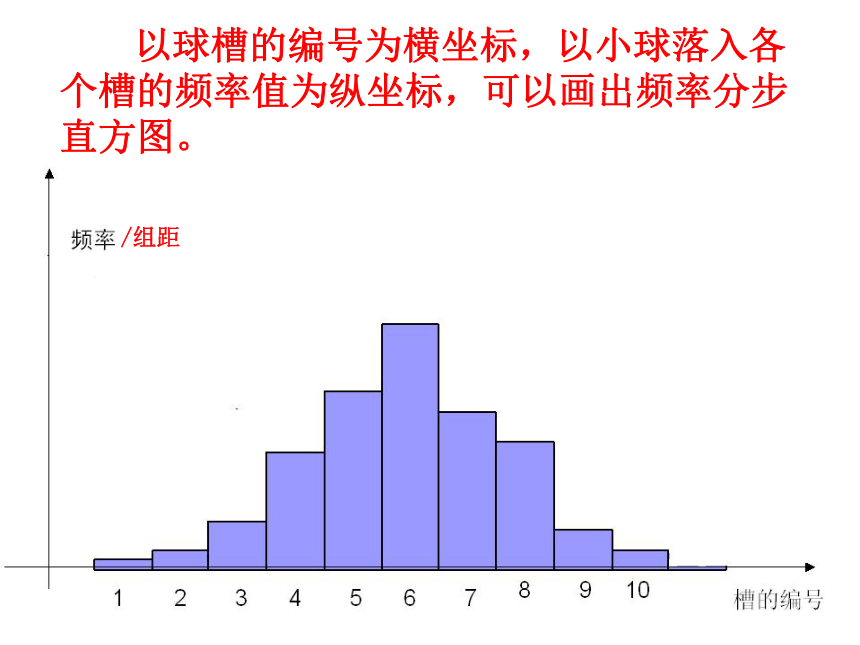
/组距
以球槽的编号为横坐标,以小球落入各个槽的频率值为纵坐标,可以画出频率分步直方图。
0
Y
X
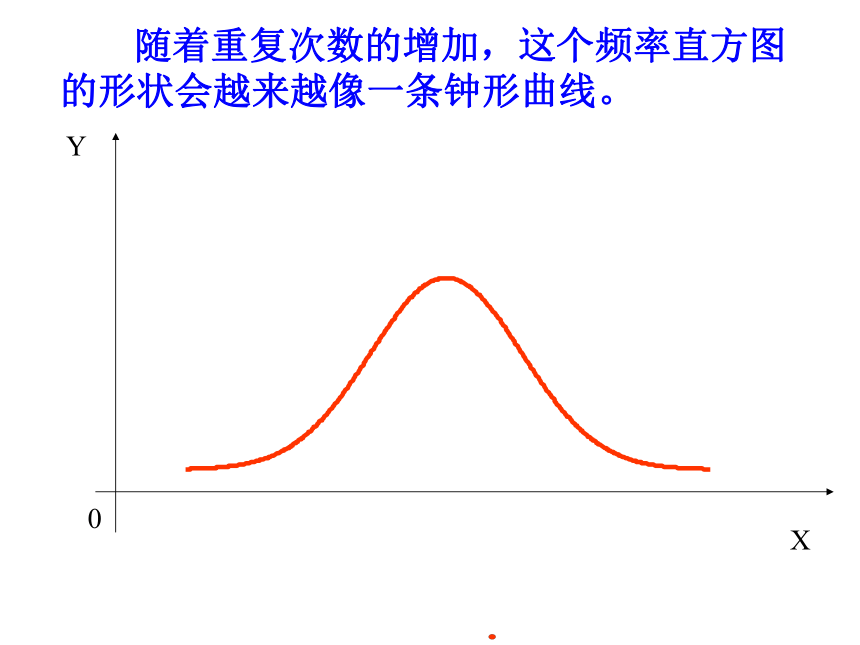
随着重复次数的增加,这个频率直方图的形状会越来越像一条钟形曲线。
这条曲线就是(或近似地是)以下函数的图象:
练习:给出下列两个正态分布密度函数的表达式,请找出其均值m和标准差s
m=0 , s =1
m=1 , s =2
正态分布的定义:
如果对于任何实数 a 则称为X 服从正态分布. 正态分布由参数μ、σ唯一确定.正态分布记作 N(μ,σ2).
若随机变量X服从正态分布,则
记作 X~ N(μ,σ2)
正态总体的函数表示式
当μ= 0,σ=1时
函数表示式变为:
因此,当m=0 , s =1时,X 服从标准正态分布,记为X~N (0 , 1)
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,在正常生产条件下各种产品的质量指标;
在测量中,测量结果;
在生物学中,同一群体的某一特征;……;
在气象中,某地每年七月份的平均气温、平均湿度
以及降雨量等,水文中的水位;
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
正态曲线的性质
(4)曲线与x轴之间的面积之和为1
(3)曲线在x=μ处达到峰值(最高点)
正态曲线下的面积规律
X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。
S(-?,-X)= S(X,?)
S(-x2,-x1)= S(x1,x2)
-x1 -x2 x2 x1
?
?
-x x
方差相等、均数不等的正态分布图示
?3
?1
?2
σ=0.5
μ= -1
μ=0
μ= 1
为位置参数
(5) 当σ一定时,曲线随着μ的变化而沿x轴平移;
均数相等、方差不等的正态分布图示
?
?=0.5
?=1
?=2
μ=0
为形状参数
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
特殊区间的概率:
若X~N ,则对于任何实数a>0,概率
m-a
m+a
x=μ
阴影部分的面积,对于固定的 和 而言,该面积随着的 减少而变大,这说明 越小,随机变量落在区间 的概率越大,即集中在均值 周围的概率越大。
我们从上图看到,正态总体在 以外取值的概率只有4.6%,在 以外取值的概率只有0.3 %。
特别地有
做练习:
1、P74第1、3题
2、P75 A组第2题
B组第2题
作业布置:
1、完成《全优课堂》
2、预习新课3.1
归纳小结
1.正态曲线及其性质;
2.正态分布及概率计算;
3.3s原则。
P75 B组 第2题:
设X~N(5,1),求P(62、在某次数学考试中,考生的成绩 服从一个正态分布,即 ~N(90,100).
(1)试求考试成绩 位于区间(70,110)上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?
2000×0.6826≈1365人
0.9544
1、设离散型随机变量X~N(0,1),则 = ,
= .
0.5
0.9544
巩固练习:
高尔顿板试验
这个试验是英国科学家高尔顿设计的,它的试验模型如图片所示,自上端放入一个小球,任其自由下落。在下落的过程中当小球碰到钉子后从左边与从右边落下的机会相等,到下一排钉子时又是如此,最后落入底
板的某一格子里,因此任意放入一球,此球落入哪一个格子事先难以确定。但是大量试验表明:放入大量小球,最后所呈现的曲线总是雷同的,也就是说,小球落入格子中的频率趋于稳定。
/组距
以球槽的编号为横坐标,以小球落入各个槽的频率值为纵坐标,可以画出频率分步直方图。
0
Y
X
随着重复次数的增加,这个频率直方图的形状会越来越像一条钟形曲线。
这条曲线就是(或近似地是)以下函数的图象:
练习:给出下列两个正态分布密度函数的表达式,请找出其均值m和标准差s
m=0 , s =1
m=1 , s =2
正态分布的定义:
如果对于任何实数 a
若随机变量X服从正态分布,则
记作 X~ N(μ,σ2)
正态总体的函数表示式
当μ= 0,σ=1时
函数表示式变为:
因此,当m=0 , s =1时,X 服从标准正态分布,记为X~N (0 , 1)
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,在正常生产条件下各种产品的质量指标;
在测量中,测量结果;
在生物学中,同一群体的某一特征;……;
在气象中,某地每年七月份的平均气温、平均湿度
以及降雨量等,水文中的水位;
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
正态曲线的性质
(4)曲线与x轴之间的面积之和为1
(3)曲线在x=μ处达到峰值(最高点)
正态曲线下的面积规律
X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。
S(-?,-X)= S(X,?)
S(-x2,-x1)= S(x1,x2)
-x1 -x2 x2 x1
?
?
-x x
方差相等、均数不等的正态分布图示
?3
?1
?2
σ=0.5
μ= -1
μ=0
μ= 1
为位置参数
(5) 当σ一定时,曲线随着μ的变化而沿x轴平移;
均数相等、方差不等的正态分布图示
?
?=0.5
?=1
?=2
μ=0
为形状参数
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
特殊区间的概率:
若X~N ,则对于任何实数a>0,概率
m-a
m+a
x=μ
阴影部分的面积,对于固定的 和 而言,该面积随着的 减少而变大,这说明 越小,随机变量落在区间 的概率越大,即集中在均值 周围的概率越大。
我们从上图看到,正态总体在 以外取值的概率只有4.6%,在 以外取值的概率只有0.3 %。
特别地有
做练习:
1、P74第1、3题
2、P75 A组第2题
B组第2题
作业布置:
1、完成《全优课堂》
2、预习新课3.1
归纳小结
1.正态曲线及其性质;
2.正态分布及概率计算;
3.3s原则。
P75 B组 第2题:
设X~N(5,1),求P(6
(1)试求考试成绩 位于区间(70,110)上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?
2000×0.6826≈1365人
0.9544
1、设离散型随机变量X~N(0,1),则 = ,
= .
0.5
0.9544
巩固练习:
