2019-2020学年黑龙江省哈尔滨市七年级(上)期末数学试卷(五四学制)(word版含答案)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨市七年级(上)期末数学试卷(五四学制)(word版含答案) | 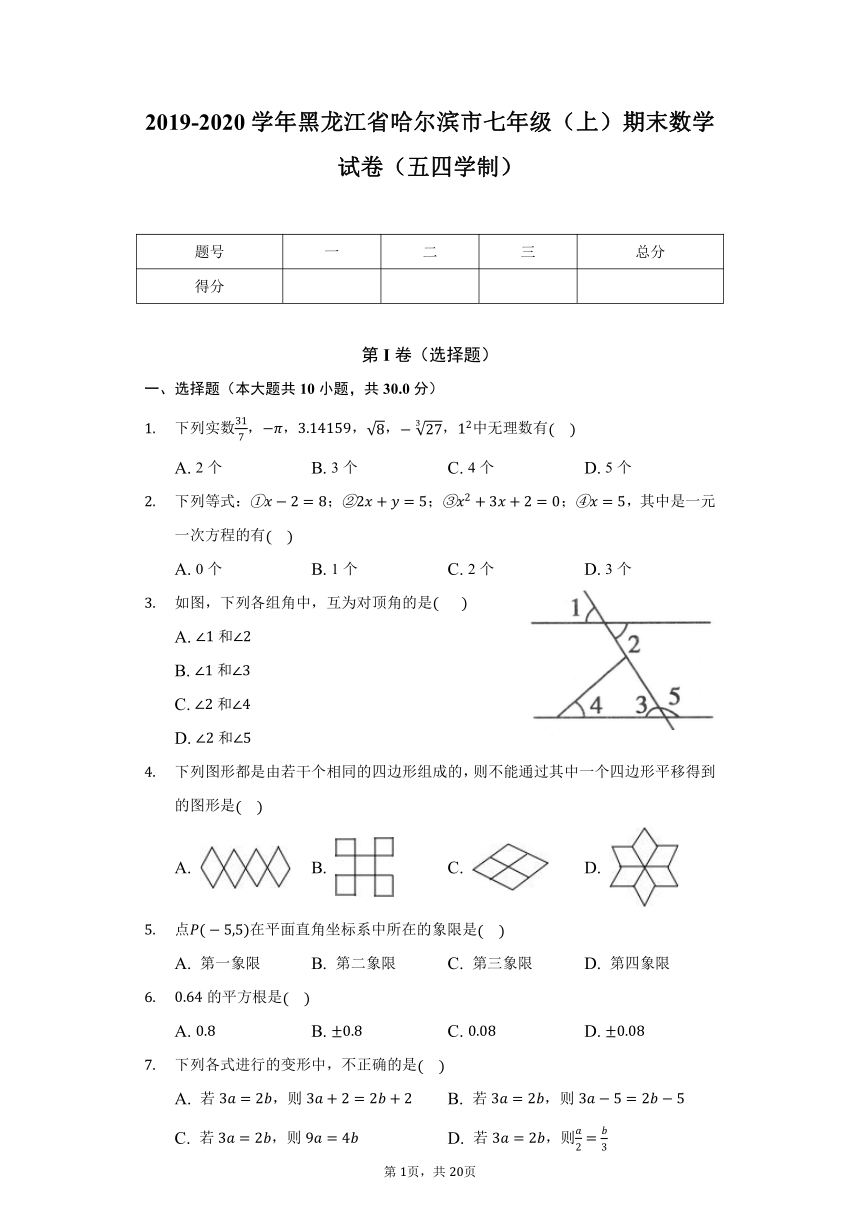 | |
| 格式 | zip | ||
| 文件大小 | 156.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 07:26:53 | ||
图片预览




文档简介
2019-2020学年黑龙江省哈尔滨市七年级(上)期末数学试卷(五四学制)
题号
一
二
三
总分
得分
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分)
下列实数,,,,,中无理数有
A.
2个
B.
3个
C.
4个
D.
5个
下列等式:;;;,其中是一元一次方程的有
A.
0个
B.
1个
C.
2个
D.
3个
如图,下列各组角中,互为对顶角的是?
?
A.
和
B.
和
C.
和
D.
和
下列图形都是由若干个相同的四边形组成的,则不能通过其中一个四边形平移得到的图形是
A.
B.
C.
D.
点在平面直角坐标系中所在的象限是
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
的平方根是
A.
B.
C.
D.
下列各式进行的变形中,不正确的是
A.
若,则
B.
若,则
C.
若,则?
D.
若,则
某车间有28名工人,每人每天能生产桌子12张或椅子18把,每天生产的桌子和椅子按配套,设有x名工人生产桌子,其他人生产椅子,则所列方程正确的是
A.
B.
C.
D.
如图,下列能判定的条件有个
?
.
A.
1
B.
2
C.
3
D.
4
下列选项中可以用来说明命题“若,则”是假命题的反例是?
?
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共10小题,共30.0分)
的立方根是__________.
比较大小:??????????填“”“”或“”
已知是关于x的一元一次方程的解,则的值是______.
将命题“对顶角相等”改为如果那么的形式________.
在平面直角坐标系中,点P?在x轴上,则______.
如图,已知,,::3,则的度数为______.
如图,,,DB平分,则的度数为______.
某种商品每件的标价是270元,按标价的八折销售时,仍可获利,则这种商品每件的进价为______元.
已知,,,则的面积是___________.
如图,将一张长方形纸条沿某条直线折叠,已知,则_________.
三、解答题(本大题共7小题,共60.0分)
计算:
解方程;
如图,在正方形网格中,每个小正方形的边长均为1个单位,格点三角形顶点是网格线的交点的三角形的顶点A,C的坐标分别为,.
???
请在图所示的网格内建立平面直角坐标系.
???
把三角形ABC先向右平移5个单位,再向下平移3个单位,得到三角形,请在图中画出三角形,并写出点,,的坐标.
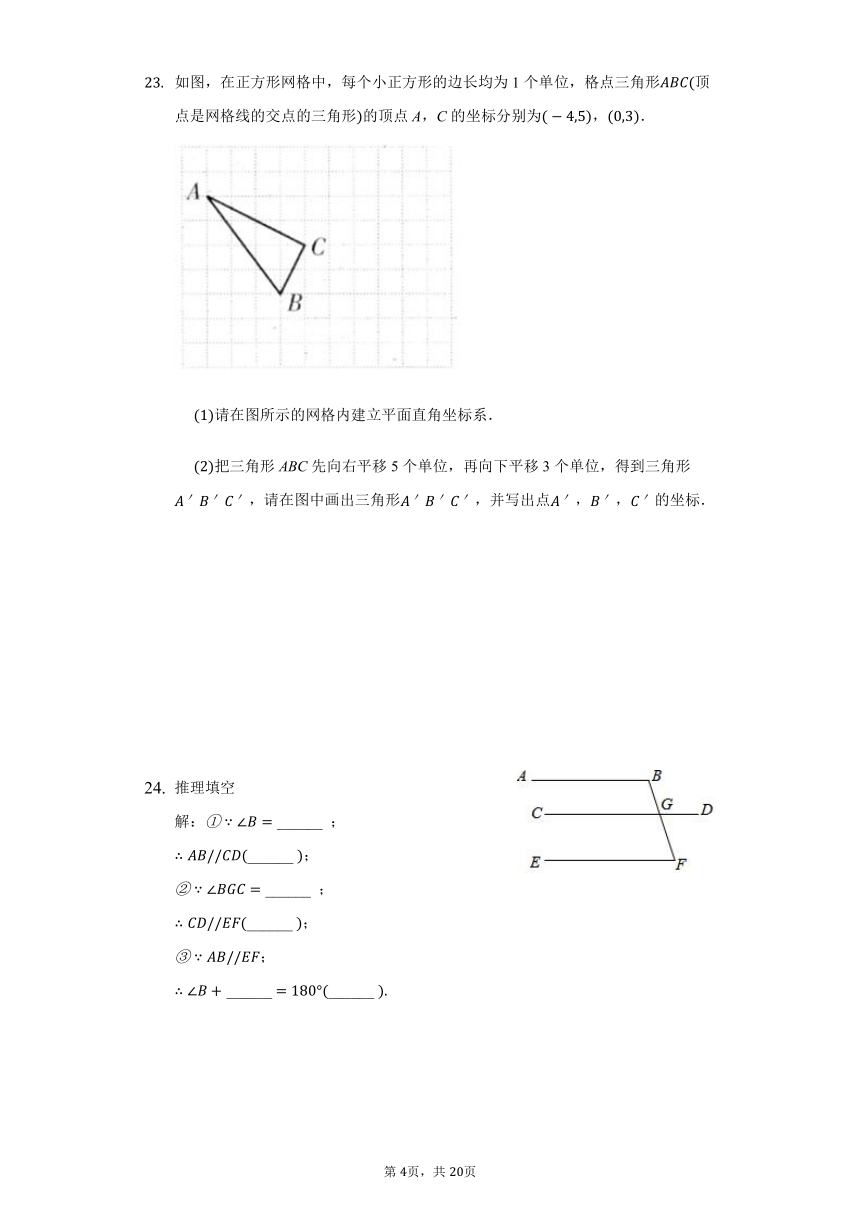
推理填空
解:
______
;
______
;
______
;
______
;
;
______
______
某市为了鼓励节约用水,对某用水行业的用水收费标准作出了如下规定:每户每月用水不超过10t的部分,按每吨元收费;超过10t而不超过20t的部分,按每吨元收取;超过20t的部分,则按每吨8元收取.
今有一用户按此标准10月份用水27t,该用户当月应缴_______元水费.
今有一用户按此标准11月份缴120元水费,问该用户11月份用水多少吨?表示吨
如图,,点G在CD上,GE交AB于F,于点E,GH平分,若,求的度数.
如图,平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,点B在x轴的正半轴上,以AB为斜边向上作等腰直角,BC交y轴于点D,.
如图1,求点B的坐标;
如图2,动点E从点O出发以每秒1个单位长度的速度沿y轴的正半轴运动,设运动时间为t秒,连接CE,设的面积为S,请用含t的式子来表示S;
如图3,在的条件下,当点E在OD的延长线上时,点F在直线CE的下方,且,连接AD,取AD的中点M,连接FM并延长交AO于点N,连接FO,当时,求S的值.
答案和解析
1.【答案】A
【解析】
【分析】
本题主要考查了无理数的概念,无限不循环小数叫做无理数,常见类型有:,等;开方开不尽的数;,等有这样规律的数。理解无理数的概念是解本题的关键注意区分无理数与有理数的概念,整数和分数统称为有理数,即有限小数和无限循环小数均是有理数;无限不循环小数叫做无理数。根据有理数和无理数的概念逐一辨别即可得出答案.
【解答】
解:无理数有,共2个.
故选A.
2.【答案】C
【解析】解:是一元一次方程;
含有两个未知数,不是一元一次方程;
未知数的最高次数为2,不是一元一次方程;
是一元一次方程.
故选:C.
根据一元一次方程的定义判断即可.
本题主要考查的是一元一次方程的定义,掌握一元一次方程的定义是解题的关键.
3.【答案】A
【解析】
【分析】
本题主要考查对顶角的定义根据对顶角的定义,如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角即可解答.
【解答】
A.和是对顶角,故A正确;
B.和不符合对顶角定义,不是对顶角,故B错误;
C.和不符合对顶角定义,不是对顶角,故C错误;
D.和不符合对顶角定义,不是对顶角,故D错误;
故选A.
4.【答案】D
【解析】
【分析】
本题考查的是利用平移设计图案以及平移的性质,熟知图形的平移只改变图形的位置,而不改变图形的形状和大小是解答此题的关键.
根据平移与旋转的性质即可得出结论.
【解答】
解:能通过其中一个四边形平移得到,不合题意;
B.能通过其中一个四边形平移得到,不合题意;
C.能通过其中一个四边形平移得到,不合题意;
D.不能通过其中一个四边形平移得到,需要一个四边形旋转得到,符合题意.
故选D.
5.【答案】B
【解析】
【分析】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号特征是解决本题的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限根据各象限内点的坐标特征解答即可.
【解答】
解:点在第二象限.
故选:B.
6.【答案】B
【解析】解:的平方根是.
故选:B.
依据平方根的定义求解即可.
本题主要考查的是平方根的定义,熟练掌握平方根的定义是解题的关键.
7.【答案】C
【解析】
【分析】
此题主要考查了等式的性质和应用,要熟练掌握,解答此题的关键是要明确:等式两边加同一个数或式子,结果仍得等式.等式两边乘同一个数或除以一个不为零的数,结果仍得等式根据等式的性质,逐项判断即可.
【解答】
解:,
,
选项A正确;
,
,
选项B正确;
,
,
选项C不正确;
,
,
选项D正确.
故选C.
8.【答案】C
【解析】
【分析】
本题考查一元一次方程在实际问题中的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.根据椅子的个数桌子个数列方程.
【解答】
解:设分配x人生产桌子,则有人生产椅子,由题意得:
.
故选C.
9.【答案】C
【解析】解:,
;
,
;
,
;
?,
.
故选:C.
根据平行线的判定方法对四个条件分别进行判断即可.
本题考查了平行线判定:同位角相等,两直线平行;同旁内角互补,两直线平行;内错角相等,两直线平行.
10.【答案】D
【解析】
【分析】
本题考查了命题与定理,要证明一个命题是假命题的反例,只需要这个例子满足命题的题设,但不满足命题的结论即可,据此逐一判断各选项即可得解.
【解答】
解:A、不满足,不是题设的条件,不是特例,故不是反例;
B、不满足,不是题设的条件,不是特例,故不是反例;
C、满足,也满足,故不是反例;
D、满足,不满足的要求,故是原命题的反例.
故选D.
11.【答案】
【解析】
【分析】
本题主要考查了立方根的概念.如果一个数x的立方等于a,即x的三次方等于,那么这个数x就叫做a的立方根,也叫做三次方根.读作“三次根号a”其中,a叫做被开方数,3叫做根指数,利用立方根的定义即可求解.
【解答】
解:,?
的立方根是,
的立方根是?
故答案为.
12.【答案】
【解析】
【分析】
本题考查了实数大小比较,将根号外面的数字转化到根号里面是解题的关键将根号外面的2平方后放到根号里面,再进行比较即可.
【解答】
解:,,
,
故填.
13.【答案】2
【解析】
【分析】
本题考查了一元一次方程的解,正确掌握解一元一次方程的方法是解题的关键把代入方程得到关于m的一元一次方程,解之,得到m的值,代入,计算求值即可.
【解答】
解:把代入方程得:
,
解得:,
,
故答案为2.
14.【答案】如果两个角互为对顶角,那么这两个角相等
【解析】
【分析】
本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单先找到命题的题设和结论,再写成“如果,那么”的形式即可.
【解答】
解:原命题的条件是:“两个角是对顶角”,结论是:“这两个角相等”,
命题“对顶角相等”写成“如果,那么”的形式为:“如果两个角互为对顶角,那么这两个角相等”.
故答案为如果两个角互为对顶角,那么这两个角相等.
15.【答案】0
【解析】解:点P?在x轴上,
.
故答案为:0.
直接利用x轴上点的坐标特点得出答案.
此题主要考查了点的坐标,正确掌握x轴点的坐标特点是解题关键.
16.【答案】
【解析】解:,,
,
,
::3,
,
.
故答案为:
直接利用垂直的定义结合::3求出,再根据角的和差关系求解即可.
此题主要考查了垂线以及角的计算,正确得出是解题关键.
17.【答案】
【解析】解:,
,
平分,
,
,
,
则的度数为:.
故答案为:.
直接利用平行线的性质以及角平分线的性质得出,进而得出答案.
此题主要考查了平行线的性质,正确得出的度数是解题关键.
18.【答案】180
【解析】解:设这种商品每件的进价为x元,
,
解得,,
故答案为:180.
根据题意可以列出相应的方程,本题得以解决.
本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程.
19.【答案】6
【解析】
【分析】
本题主要考查了坐标与图形的性质,正确得出的高是解题关键.?根据题意得出AB的长以及的高进而求出答案.
【解答】
解:点,,,
分别过点A、B作轴于E,轴于D,过点C作轴,交AE、BD于F、G,如图所示
则,,,,,
,
,,
所以,
故答案为6.
20.【答案】58
【解析】
【分析】
本题考查平行线的性质,翻折变换知识,解题的关键是熟练掌握基本知识依据平行线的性质以及折叠的性质,即可得到的度数.
【解答】
解:如图,
,
,
由折叠可得,,
,
.
故答案为58.
21.【答案】解:原式
.
【解析】首先化简二次根式进而合并同类二次根式即可.
此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.
22.【答案】?
;
【解析】
【分析】
先去括号,然后移项,合并同类项,系数化为1即可;
先两边乘以12去掉分母,然后按照去括号、移项、合并同类项、系数化为1的步骤解答即可.
【详解】
解:去括号得:
移项得:
合并同类项得:
系数化为1得:;
去分母得:
去括号得:
移项并合并得:.
【点睛】
本题考查了一元一次方程的解法,解一元一次方程的一般步骤是:去分母,去括号,移项,合并同类项,系数化为1.
23.【答案】解:如图所示:平面直角坐标系即为所求;
如图所示:即为所求,,,.
【解析】本题考查的是作图平移有关知识.
直接利用A,C点坐标进而建立平面直角坐标系即可;
利用平移的性质分别得出对应点位置进而得出答案.
24.【答案】;内错角相等,两直线平行;
;同位角相等,两直线平行;
;两直线平行,同旁内角互补
【解析】解:,
?内错角相等,两直线平行,
故答案为:,内错角相等,两直线平行;
,
同位角相等,两直线平行;
故答案为;,同位角相等,两直线平行;
,
两直线平行,同旁内角互补,
故答案为:,两直线平行,同旁内角互补.
根据平行线的判定得出即可;
根据平行线的判定得出即可;
根据平行线的性质得出即可.
本题考查了平行线的性质和判定,能灵活运用定理进行推理是解此题的关键.
25.【答案】解:元;
当月用水20t时,应缴水费?元元,
该用户11月份用水超过20t.
设该用户11月份用水.
由题意得:,
解得.
答:该用户11月份用水25t.
【解析】
【分析】
本题主要考查的是有理数的混合运算,一元一次方程的应用的有关知识.
根据题意列出式子求解即可;
当月用水20t时,应缴水费?元元,所以该用户11月份用水超过设该用户11月份用水根据题意列出方程,求解即可.
【解答】
解:元,
故答案为136;
见答案.
26.【答案】解:于点E,,
,
,
,
,
又平分,
.
【解析】本题考查了平行线的性质、三角形内角和定理、角平分线定义等知识点,能根据知识点求出的度数是解此题的关键.
依据于点E,,可得,依据,可得,进而得出,再根据GH平分,即可得到的度数.
27.【答案】解:如图1中,作于H.
,
,,
,,
,
,
,
,
,
,.
由可知,
所以当时,
当时,,
综上所述,.
如图3中,延长AC交y轴于H,连接FD,.
,是等腰直角三角形,
,
由知,
,,
是等腰直角三角形,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
又,
≌,
,,
,
,
,
,
是AD中点,
,
又,
≌,
,
,
≌,
,
,
,
,
,
,
,
.
【解析】如图1中,作于理由等腰直角三角形的性质求出OB即可.
根据点D的坐标,分两种情形求解.
如图3中,延长AC交y轴于H,连接证明≌,推出,,证明≌,推出,由,推出≌,推出,,推出,由,推出,方程解决问题.
本题属于三角形综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质三角形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.
第2页,共2页
第1页,共1页
题号
一
二
三
总分
得分
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分)
下列实数,,,,,中无理数有
A.
2个
B.
3个
C.
4个
D.
5个
下列等式:;;;,其中是一元一次方程的有
A.
0个
B.
1个
C.
2个
D.
3个
如图,下列各组角中,互为对顶角的是?
?
A.
和
B.
和
C.
和
D.
和
下列图形都是由若干个相同的四边形组成的,则不能通过其中一个四边形平移得到的图形是
A.
B.
C.
D.
点在平面直角坐标系中所在的象限是
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
的平方根是
A.
B.
C.
D.
下列各式进行的变形中,不正确的是
A.
若,则
B.
若,则
C.
若,则?
D.
若,则
某车间有28名工人,每人每天能生产桌子12张或椅子18把,每天生产的桌子和椅子按配套,设有x名工人生产桌子,其他人生产椅子,则所列方程正确的是
A.
B.
C.
D.
如图,下列能判定的条件有个
?
.
A.
1
B.
2
C.
3
D.
4
下列选项中可以用来说明命题“若,则”是假命题的反例是?
?
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共10小题,共30.0分)
的立方根是__________.
比较大小:??????????填“”“”或“”
已知是关于x的一元一次方程的解,则的值是______.
将命题“对顶角相等”改为如果那么的形式________.
在平面直角坐标系中,点P?在x轴上,则______.
如图,已知,,::3,则的度数为______.
如图,,,DB平分,则的度数为______.
某种商品每件的标价是270元,按标价的八折销售时,仍可获利,则这种商品每件的进价为______元.
已知,,,则的面积是___________.
如图,将一张长方形纸条沿某条直线折叠,已知,则_________.
三、解答题(本大题共7小题,共60.0分)
计算:
解方程;
如图,在正方形网格中,每个小正方形的边长均为1个单位,格点三角形顶点是网格线的交点的三角形的顶点A,C的坐标分别为,.
???
请在图所示的网格内建立平面直角坐标系.
???
把三角形ABC先向右平移5个单位,再向下平移3个单位,得到三角形,请在图中画出三角形,并写出点,,的坐标.
推理填空
解:
______
;
______
;
______
;
______
;
;
______
______
某市为了鼓励节约用水,对某用水行业的用水收费标准作出了如下规定:每户每月用水不超过10t的部分,按每吨元收费;超过10t而不超过20t的部分,按每吨元收取;超过20t的部分,则按每吨8元收取.
今有一用户按此标准10月份用水27t,该用户当月应缴_______元水费.
今有一用户按此标准11月份缴120元水费,问该用户11月份用水多少吨?表示吨
如图,,点G在CD上,GE交AB于F,于点E,GH平分,若,求的度数.
如图,平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,点B在x轴的正半轴上,以AB为斜边向上作等腰直角,BC交y轴于点D,.
如图1,求点B的坐标;
如图2,动点E从点O出发以每秒1个单位长度的速度沿y轴的正半轴运动,设运动时间为t秒,连接CE,设的面积为S,请用含t的式子来表示S;
如图3,在的条件下,当点E在OD的延长线上时,点F在直线CE的下方,且,连接AD,取AD的中点M,连接FM并延长交AO于点N,连接FO,当时,求S的值.
答案和解析
1.【答案】A
【解析】
【分析】
本题主要考查了无理数的概念,无限不循环小数叫做无理数,常见类型有:,等;开方开不尽的数;,等有这样规律的数。理解无理数的概念是解本题的关键注意区分无理数与有理数的概念,整数和分数统称为有理数,即有限小数和无限循环小数均是有理数;无限不循环小数叫做无理数。根据有理数和无理数的概念逐一辨别即可得出答案.
【解答】
解:无理数有,共2个.
故选A.
2.【答案】C
【解析】解:是一元一次方程;
含有两个未知数,不是一元一次方程;
未知数的最高次数为2,不是一元一次方程;
是一元一次方程.
故选:C.
根据一元一次方程的定义判断即可.
本题主要考查的是一元一次方程的定义,掌握一元一次方程的定义是解题的关键.
3.【答案】A
【解析】
【分析】
本题主要考查对顶角的定义根据对顶角的定义,如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角即可解答.
【解答】
A.和是对顶角,故A正确;
B.和不符合对顶角定义,不是对顶角,故B错误;
C.和不符合对顶角定义,不是对顶角,故C错误;
D.和不符合对顶角定义,不是对顶角,故D错误;
故选A.
4.【答案】D
【解析】
【分析】
本题考查的是利用平移设计图案以及平移的性质,熟知图形的平移只改变图形的位置,而不改变图形的形状和大小是解答此题的关键.
根据平移与旋转的性质即可得出结论.
【解答】
解:能通过其中一个四边形平移得到,不合题意;
B.能通过其中一个四边形平移得到,不合题意;
C.能通过其中一个四边形平移得到,不合题意;
D.不能通过其中一个四边形平移得到,需要一个四边形旋转得到,符合题意.
故选D.
5.【答案】B
【解析】
【分析】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号特征是解决本题的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限根据各象限内点的坐标特征解答即可.
【解答】
解:点在第二象限.
故选:B.
6.【答案】B
【解析】解:的平方根是.
故选:B.
依据平方根的定义求解即可.
本题主要考查的是平方根的定义,熟练掌握平方根的定义是解题的关键.
7.【答案】C
【解析】
【分析】
此题主要考查了等式的性质和应用,要熟练掌握,解答此题的关键是要明确:等式两边加同一个数或式子,结果仍得等式.等式两边乘同一个数或除以一个不为零的数,结果仍得等式根据等式的性质,逐项判断即可.
【解答】
解:,
,
选项A正确;
,
,
选项B正确;
,
,
选项C不正确;
,
,
选项D正确.
故选C.
8.【答案】C
【解析】
【分析】
本题考查一元一次方程在实际问题中的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.根据椅子的个数桌子个数列方程.
【解答】
解:设分配x人生产桌子,则有人生产椅子,由题意得:
.
故选C.
9.【答案】C
【解析】解:,
;
,
;
,
;
?,
.
故选:C.
根据平行线的判定方法对四个条件分别进行判断即可.
本题考查了平行线判定:同位角相等,两直线平行;同旁内角互补,两直线平行;内错角相等,两直线平行.
10.【答案】D
【解析】
【分析】
本题考查了命题与定理,要证明一个命题是假命题的反例,只需要这个例子满足命题的题设,但不满足命题的结论即可,据此逐一判断各选项即可得解.
【解答】
解:A、不满足,不是题设的条件,不是特例,故不是反例;
B、不满足,不是题设的条件,不是特例,故不是反例;
C、满足,也满足,故不是反例;
D、满足,不满足的要求,故是原命题的反例.
故选D.
11.【答案】
【解析】
【分析】
本题主要考查了立方根的概念.如果一个数x的立方等于a,即x的三次方等于,那么这个数x就叫做a的立方根,也叫做三次方根.读作“三次根号a”其中,a叫做被开方数,3叫做根指数,利用立方根的定义即可求解.
【解答】
解:,?
的立方根是,
的立方根是?
故答案为.
12.【答案】
【解析】
【分析】
本题考查了实数大小比较,将根号外面的数字转化到根号里面是解题的关键将根号外面的2平方后放到根号里面,再进行比较即可.
【解答】
解:,,
,
故填.
13.【答案】2
【解析】
【分析】
本题考查了一元一次方程的解,正确掌握解一元一次方程的方法是解题的关键把代入方程得到关于m的一元一次方程,解之,得到m的值,代入,计算求值即可.
【解答】
解:把代入方程得:
,
解得:,
,
故答案为2.
14.【答案】如果两个角互为对顶角,那么这两个角相等
【解析】
【分析】
本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单先找到命题的题设和结论,再写成“如果,那么”的形式即可.
【解答】
解:原命题的条件是:“两个角是对顶角”,结论是:“这两个角相等”,
命题“对顶角相等”写成“如果,那么”的形式为:“如果两个角互为对顶角,那么这两个角相等”.
故答案为如果两个角互为对顶角,那么这两个角相等.
15.【答案】0
【解析】解:点P?在x轴上,
.
故答案为:0.
直接利用x轴上点的坐标特点得出答案.
此题主要考查了点的坐标,正确掌握x轴点的坐标特点是解题关键.
16.【答案】
【解析】解:,,
,
,
::3,
,
.
故答案为:
直接利用垂直的定义结合::3求出,再根据角的和差关系求解即可.
此题主要考查了垂线以及角的计算,正确得出是解题关键.
17.【答案】
【解析】解:,
,
平分,
,
,
,
则的度数为:.
故答案为:.
直接利用平行线的性质以及角平分线的性质得出,进而得出答案.
此题主要考查了平行线的性质,正确得出的度数是解题关键.
18.【答案】180
【解析】解:设这种商品每件的进价为x元,
,
解得,,
故答案为:180.
根据题意可以列出相应的方程,本题得以解决.
本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程.
19.【答案】6
【解析】
【分析】
本题主要考查了坐标与图形的性质,正确得出的高是解题关键.?根据题意得出AB的长以及的高进而求出答案.
【解答】
解:点,,,
分别过点A、B作轴于E,轴于D,过点C作轴,交AE、BD于F、G,如图所示
则,,,,,
,
,,
所以,
故答案为6.
20.【答案】58
【解析】
【分析】
本题考查平行线的性质,翻折变换知识,解题的关键是熟练掌握基本知识依据平行线的性质以及折叠的性质,即可得到的度数.
【解答】
解:如图,
,
,
由折叠可得,,
,
.
故答案为58.
21.【答案】解:原式
.
【解析】首先化简二次根式进而合并同类二次根式即可.
此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.
22.【答案】?
;
【解析】
【分析】
先去括号,然后移项,合并同类项,系数化为1即可;
先两边乘以12去掉分母,然后按照去括号、移项、合并同类项、系数化为1的步骤解答即可.
【详解】
解:去括号得:
移项得:
合并同类项得:
系数化为1得:;
去分母得:
去括号得:
移项并合并得:.
【点睛】
本题考查了一元一次方程的解法,解一元一次方程的一般步骤是:去分母,去括号,移项,合并同类项,系数化为1.
23.【答案】解:如图所示:平面直角坐标系即为所求;
如图所示:即为所求,,,.
【解析】本题考查的是作图平移有关知识.
直接利用A,C点坐标进而建立平面直角坐标系即可;
利用平移的性质分别得出对应点位置进而得出答案.
24.【答案】;内错角相等,两直线平行;
;同位角相等,两直线平行;
;两直线平行,同旁内角互补
【解析】解:,
?内错角相等,两直线平行,
故答案为:,内错角相等,两直线平行;
,
同位角相等,两直线平行;
故答案为;,同位角相等,两直线平行;
,
两直线平行,同旁内角互补,
故答案为:,两直线平行,同旁内角互补.
根据平行线的判定得出即可;
根据平行线的判定得出即可;
根据平行线的性质得出即可.
本题考查了平行线的性质和判定,能灵活运用定理进行推理是解此题的关键.
25.【答案】解:元;
当月用水20t时,应缴水费?元元,
该用户11月份用水超过20t.
设该用户11月份用水.
由题意得:,
解得.
答:该用户11月份用水25t.
【解析】
【分析】
本题主要考查的是有理数的混合运算,一元一次方程的应用的有关知识.
根据题意列出式子求解即可;
当月用水20t时,应缴水费?元元,所以该用户11月份用水超过设该用户11月份用水根据题意列出方程,求解即可.
【解答】
解:元,
故答案为136;
见答案.
26.【答案】解:于点E,,
,
,
,
,
又平分,
.
【解析】本题考查了平行线的性质、三角形内角和定理、角平分线定义等知识点,能根据知识点求出的度数是解此题的关键.
依据于点E,,可得,依据,可得,进而得出,再根据GH平分,即可得到的度数.
27.【答案】解:如图1中,作于H.
,
,,
,,
,
,
,
,
,
,.
由可知,
所以当时,
当时,,
综上所述,.
如图3中,延长AC交y轴于H,连接FD,.
,是等腰直角三角形,
,
由知,
,,
是等腰直角三角形,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
又,
≌,
,,
,
,
,
,
是AD中点,
,
又,
≌,
,
,
≌,
,
,
,
,
,
,
,
.
【解析】如图1中,作于理由等腰直角三角形的性质求出OB即可.
根据点D的坐标,分两种情形求解.
如图3中,延长AC交y轴于H,连接证明≌,推出,,证明≌,推出,由,推出≌,推出,,推出,由,推出,方程解决问题.
本题属于三角形综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质三角形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.
第2页,共2页
第1页,共1页
同课章节目录
