高中数学人教A版选修2-3第三章:3.1回归分析的基本思想及其初步应用 课件(28张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-3第三章:3.1回归分析的基本思想及其初步应用 课件(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1016.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览






文档简介
3.1 回归分析的基本思想及其初步应用
两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
复习:一、两个变量间的关系
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系.
函数关系中的两个变量间是一种确定性关系,函数关系是一种理想的关系模型
相关关系是一种非确定性关系,相关关系在现实生活中大量存在,是更一般的情况。
现实生活中存在着大量的相关关系:
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
二、两个变量的线性相关
(1)散点图
正相关、
负相关。
(2)回归直线:观察散点图的特征,如果各点大致分布在一条直线的附近,就称两个变量之间具有线性相关的关系,这条直线叫做回归直线。
三、回归直线方程:最小二乘法
1、所求回归直线方程为 ,其中:
称为样本点的中心
2、求线性回归直线方程的步骤:
第一步:列表(把数据整理成表格);
第二步:计算:
第三步:代入公式计算b,a的值;
第四步:写出直线方程:
对两个变量进行的线性分析叫做线性回归分析。
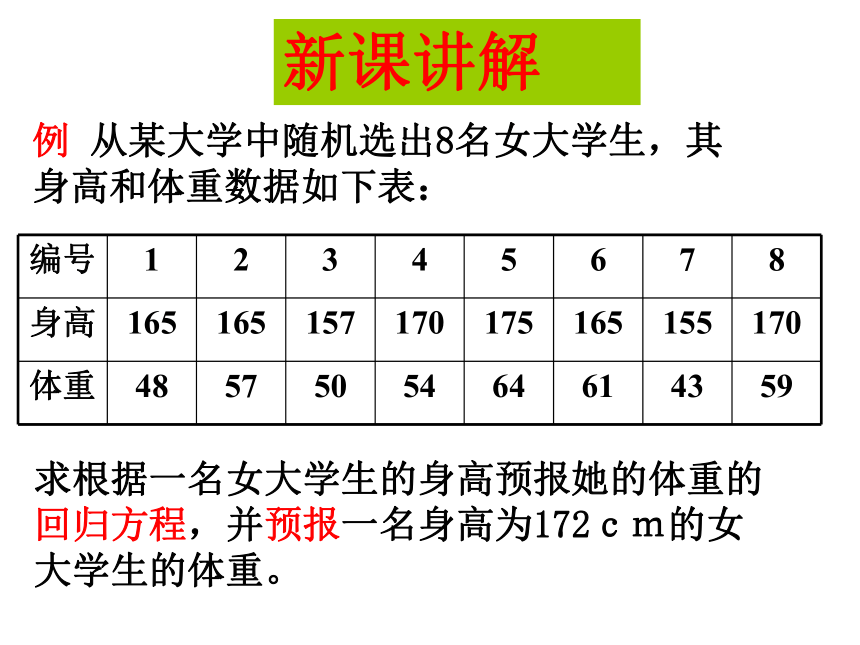
例 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号
1
2
3
4
5
6
7
8
身高
165
165
157
170
175
165
155
170
体重
48
57
50
54
64
61
43
59
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
新课讲解
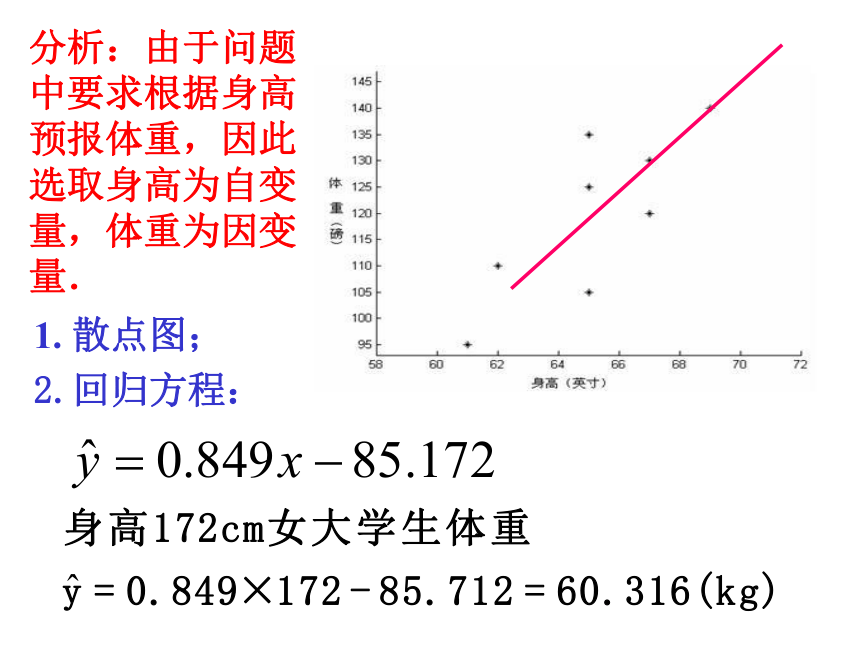
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
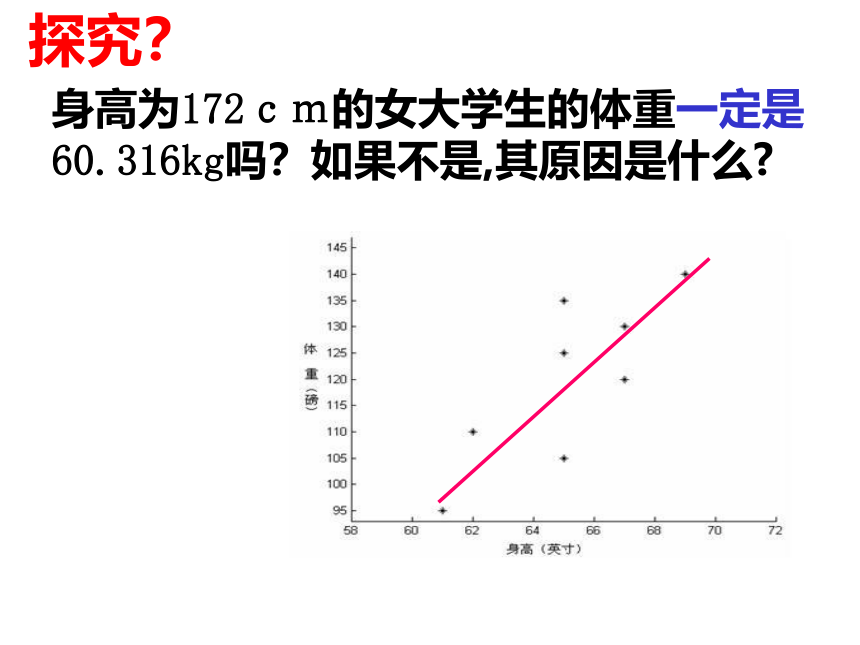
探究?
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,其原因是什么?
从散点图可以看到,样本点散布在某一条直线的附近,而不是一条直线上,所以不能用一次函数y=bx+a来描述它们之间的关系。
这时我们用下面的线性回归模型来描述身高和体重的关系:y=bx+a+e
其中a和b为模型的未知参数,
e是y与 之间的误差,通常e称为随机误差。
产生随机误差e的原因是什么?
(1)所用确定性函数模拟不恰当;
(2)忽略了某些因素的影响;
(3)观测误差,如使用的测量工具不同等。
线性回归直线与线性回归模型之间的差别
线性回归直线: y=bx+a
线性回归模型y=bx+a+e增加了随机误差项e,因变量y 的值由自变量x和随机误差项e 共同确定,即自变量x 只能解析部分y 的变化.
在统计中,我们也把自变量x称为解析变量,
因变量y称为预报变量.
线性回归模型: y=bx+a+e
解析变量x(身高)
随机误差e
预报变量y(体重)
在线性回归模型中,e是用bx+a预报真实值y的随机误差,即 e=y-(bx+a),它是一个不可观测的量,那么应如何研究随机误差呢?
随机误差的估计值为:
对于样本点:
随机误差的估计值为:
称为相应于点 的残差.
判断模型拟合的效果(精度)方法一:残差分析
在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否是线性相关,是否可以用线性回归模型来拟合数据。然后,可以通过残差 来判断模型拟合的效果,判断原始数据中是否存在可疑数据.这方面的分析工作称为残差分析。
通常先求出各个残差数据,然后画出残差图进行分析。
残差图的制作:
坐标纵轴为残差,横轴可以选择为样本编号、或身高数据、或体重估计值等等。
我们通常采用样本编号作为残差图的横轴。
判断方法:
如果残差图中的点比较均匀的分布在以横轴为中心的带形区域,说明选用的模型比较适合,带状区域宽度越窄,说明模型的拟合精度越高,回归方程的预报精度就越高!
0.382
-2.883
6.627
1.137
-4.618
2.419
2.627
-6.373
残差
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
下表为女大学生身高和体重的原始数据以及相应的残差数据:
?
e
以纵坐标为残差,横坐标为编号,作出图形(残差图)来分析残差特性.
由图可知,第1个样本点和第6个样本点的残差比较大,需要确认在采集这两个样本点的过程中是否有人为的错误.如果数据采集有错误,就予以纠正,然后重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他原因.
计算相关指数:
判断方法: R2表示解释变量对于预报变量变化的贡献率, R2越接近1,表示回归的效果越好。另一方面, R2取值越大,则残差平方和越小,即模型的拟合效果越好.
判断模型拟合的效果(精度)方法二:
其中,
称为总体偏差平方和,为确定的数值
称为残差平方和
1.线性回归方程:
2.样本点中心
称为样本点中心,回归直线 过样本点中心.
b=
a=
小 结
3.如果两个变量线性相关,则可以用线性回归模型来表示:y=bx+a+e,其中a和b为模型的未知参数, e
4.线性回归模型y=bx+a+e中,
称为随机误差。
把自变量x称为
解释变量,
把因变量y称为预报变量。
7.总偏差平方和:
5.残差:
6.残差平方和:
8.相关指数:
R2越接近1,表示回归的效果越好。另一方面, R2取值越大,则残差平方和越小,即模型的拟合效果越好.
1)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
建立回归模型的基本步骤
非线性回归分析
对于非线性回归问题,并且没有给出经验公式,这时我们可以画出已知数据的散点图,把它与学过的各种函数(幂函数、指数函数、对数函数等)的图象作比较,挑选一种跟这些散点拟合得最好的函数,然后采用适当的变量代换,把问题转化为线性回归问题,使其得到解决.
例、 一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据列于表中:
试建立产卵数y与温度x之间的回归方程。
解:(1)作散点图:
从散点图中可以看出产卵数和温度之间的关系并不能用线性回归模型来很好地近似。这些散点更像是集中在一条指数曲线或二次曲线的附近。
(指数函数模型),令
则z=bx+a,(a=lnc1,b=c2),列出变换后数据表并画出x与z 的散点图
此时x和z之间的关系可以用线性回归直线z=bx+a来拟合。由计算器得:z关于x的线性回归方程:
x
21
23
25
27
29
32
35
z
1.946
2.398
3.045
3.178
4.19
4.745
5.784
因此y关于x的非线性回归方程为
2) 用 y=c3x2+c4 模型(二次函数模型),令 ,则y=c3t+c4 ,列出变换后数据表并画出t与y 的散点图:
t
441
529
625
729
841
1024
1225
y
7
11
21
24
66
115
325
t
由计算器得:y和t之间的线性回归方程为: y=0.367t-202.54
将t=x2 代入线性回归方程得:
y=0.367x2 -202.54
函数模型
相关指数R2
线性回归模型
0.7464
二次函数模型
0.802
指数函数模型
0.98
上节例题中最好的模型是哪个?
显然,指数函数模型最好!
作业布置:
1、完成《全优课堂》
2、预习课本P91—P96内容
两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
复习:一、两个变量间的关系
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系.
函数关系中的两个变量间是一种确定性关系,函数关系是一种理想的关系模型
相关关系是一种非确定性关系,相关关系在现实生活中大量存在,是更一般的情况。
现实生活中存在着大量的相关关系:
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
二、两个变量的线性相关
(1)散点图
正相关、
负相关。
(2)回归直线:观察散点图的特征,如果各点大致分布在一条直线的附近,就称两个变量之间具有线性相关的关系,这条直线叫做回归直线。
三、回归直线方程:最小二乘法
1、所求回归直线方程为 ,其中:
称为样本点的中心
2、求线性回归直线方程的步骤:
第一步:列表(把数据整理成表格);
第二步:计算:
第三步:代入公式计算b,a的值;
第四步:写出直线方程:
对两个变量进行的线性分析叫做线性回归分析。
例 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号
1
2
3
4
5
6
7
8
身高
165
165
157
170
175
165
155
170
体重
48
57
50
54
64
61
43
59
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
新课讲解
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
探究?
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,其原因是什么?
从散点图可以看到,样本点散布在某一条直线的附近,而不是一条直线上,所以不能用一次函数y=bx+a来描述它们之间的关系。
这时我们用下面的线性回归模型来描述身高和体重的关系:y=bx+a+e
其中a和b为模型的未知参数,
e是y与 之间的误差,通常e称为随机误差。
产生随机误差e的原因是什么?
(1)所用确定性函数模拟不恰当;
(2)忽略了某些因素的影响;
(3)观测误差,如使用的测量工具不同等。
线性回归直线与线性回归模型之间的差别
线性回归直线: y=bx+a
线性回归模型y=bx+a+e增加了随机误差项e,因变量y 的值由自变量x和随机误差项e 共同确定,即自变量x 只能解析部分y 的变化.
在统计中,我们也把自变量x称为解析变量,
因变量y称为预报变量.
线性回归模型: y=bx+a+e
解析变量x(身高)
随机误差e
预报变量y(体重)
在线性回归模型中,e是用bx+a预报真实值y的随机误差,即 e=y-(bx+a),它是一个不可观测的量,那么应如何研究随机误差呢?
随机误差的估计值为:
对于样本点:
随机误差的估计值为:
称为相应于点 的残差.
判断模型拟合的效果(精度)方法一:残差分析
在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否是线性相关,是否可以用线性回归模型来拟合数据。然后,可以通过残差 来判断模型拟合的效果,判断原始数据中是否存在可疑数据.这方面的分析工作称为残差分析。
通常先求出各个残差数据,然后画出残差图进行分析。
残差图的制作:
坐标纵轴为残差,横轴可以选择为样本编号、或身高数据、或体重估计值等等。
我们通常采用样本编号作为残差图的横轴。
判断方法:
如果残差图中的点比较均匀的分布在以横轴为中心的带形区域,说明选用的模型比较适合,带状区域宽度越窄,说明模型的拟合精度越高,回归方程的预报精度就越高!
0.382
-2.883
6.627
1.137
-4.618
2.419
2.627
-6.373
残差
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
下表为女大学生身高和体重的原始数据以及相应的残差数据:
?
e
以纵坐标为残差,横坐标为编号,作出图形(残差图)来分析残差特性.
由图可知,第1个样本点和第6个样本点的残差比较大,需要确认在采集这两个样本点的过程中是否有人为的错误.如果数据采集有错误,就予以纠正,然后重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他原因.
计算相关指数:
判断方法: R2表示解释变量对于预报变量变化的贡献率, R2越接近1,表示回归的效果越好。另一方面, R2取值越大,则残差平方和越小,即模型的拟合效果越好.
判断模型拟合的效果(精度)方法二:
其中,
称为总体偏差平方和,为确定的数值
称为残差平方和
1.线性回归方程:
2.样本点中心
称为样本点中心,回归直线 过样本点中心.
b=
a=
小 结
3.如果两个变量线性相关,则可以用线性回归模型来表示:y=bx+a+e,其中a和b为模型的未知参数, e
4.线性回归模型y=bx+a+e中,
称为随机误差。
把自变量x称为
解释变量,
把因变量y称为预报变量。
7.总偏差平方和:
5.残差:
6.残差平方和:
8.相关指数:
R2越接近1,表示回归的效果越好。另一方面, R2取值越大,则残差平方和越小,即模型的拟合效果越好.
1)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
建立回归模型的基本步骤
非线性回归分析
对于非线性回归问题,并且没有给出经验公式,这时我们可以画出已知数据的散点图,把它与学过的各种函数(幂函数、指数函数、对数函数等)的图象作比较,挑选一种跟这些散点拟合得最好的函数,然后采用适当的变量代换,把问题转化为线性回归问题,使其得到解决.
例、 一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据列于表中:
试建立产卵数y与温度x之间的回归方程。
解:(1)作散点图:
从散点图中可以看出产卵数和温度之间的关系并不能用线性回归模型来很好地近似。这些散点更像是集中在一条指数曲线或二次曲线的附近。
(指数函数模型),令
则z=bx+a,(a=lnc1,b=c2),列出变换后数据表并画出x与z 的散点图
此时x和z之间的关系可以用线性回归直线z=bx+a来拟合。由计算器得:z关于x的线性回归方程:
x
21
23
25
27
29
32
35
z
1.946
2.398
3.045
3.178
4.19
4.745
5.784
因此y关于x的非线性回归方程为
2) 用 y=c3x2+c4 模型(二次函数模型),令 ,则y=c3t+c4 ,列出变换后数据表并画出t与y 的散点图:
t
441
529
625
729
841
1024
1225
y
7
11
21
24
66
115
325
t
由计算器得:y和t之间的线性回归方程为: y=0.367t-202.54
将t=x2 代入线性回归方程得:
y=0.367x2 -202.54
函数模型
相关指数R2
线性回归模型
0.7464
二次函数模型
0.802
指数函数模型
0.98
上节例题中最好的模型是哪个?
显然,指数函数模型最好!
作业布置:
1、完成《全优课堂》
2、预习课本P91—P96内容
