沪教版(上海)高中数学高二下册第十一章11.4点到直线的距离课件(14张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高二下册第十一章11.4点到直线的距离课件(14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 176.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 16:57:24 | ||
图片预览




文档简介
尝试 猜想 证明
-------------点到直线的距离
一、创设情境
我们已学习了两点间的距离公式,本节课我们来研究:点到直线的距离。
已知假定在直角坐标系上,已知一个定点 ,和一条定直线l: ,如何求点到直线的距离?
l
x
y
o
Q
方法1、过P作直线Ax+By+C=0的垂线,先求出Q的坐标,再求出|PQ|.
方法2、(启发学生)采用从特殊到一般的思想方法。我们先从点P的特殊位置考虑。点的特殊位置(1)
(2) (3)
最后考虑一般情况(4)
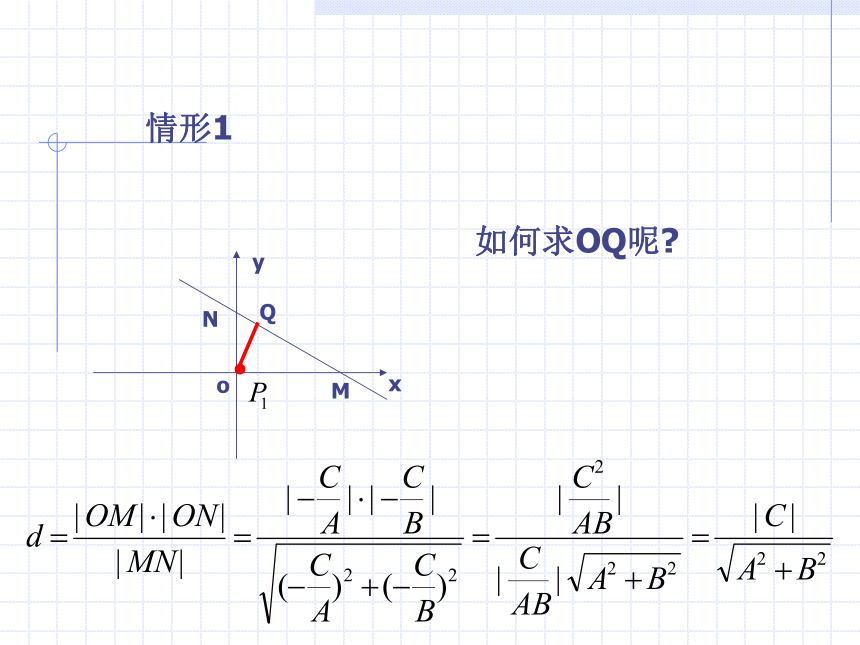
情形1
x
y
M
N
Q
o
如何求OQ呢?
x
y
o
M
S
R
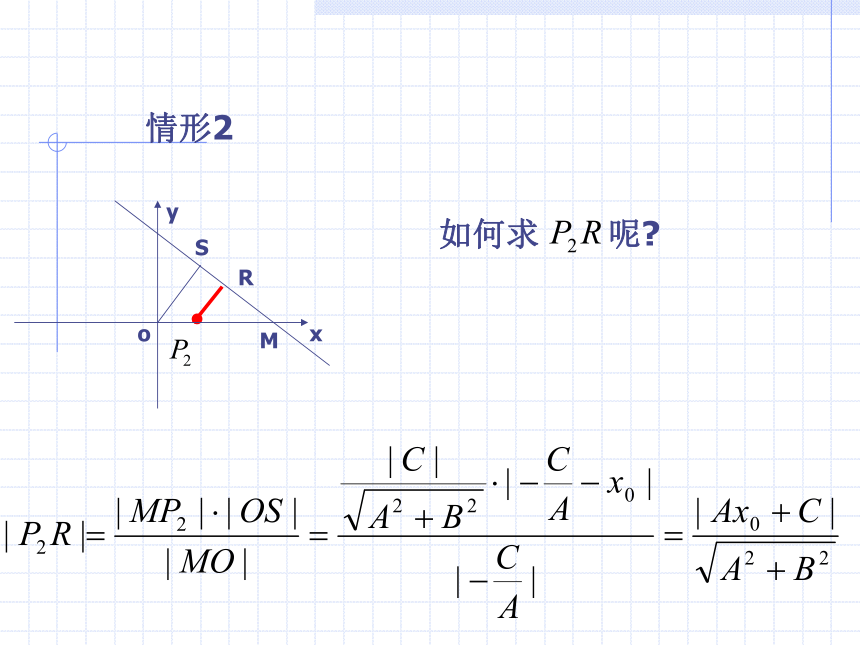
情形2
如何求 呢?
o
R
N
S
y
x
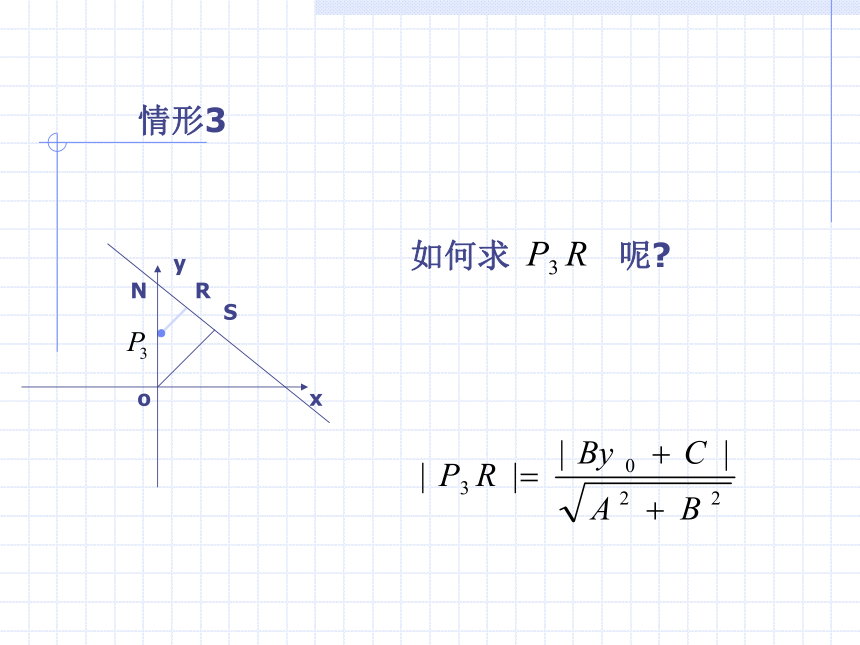
情形3
如何求 呢?
观察、归纳、猜想
我们能不能从这三种特殊情况中发现一般规律呢?
观察、类比前面三个公式,猜想出当点的坐标均不为0时,距离公式可能为
3、共同探讨
当任意一点不在坐标轴上时,如何利用前面的结论,求出P到的l距离呢?
能不能从X(或Y)轴上找一点,使它到l的距离等于 , 即能否将此距离转化为X(或Y)轴上一点到l的距离.
利用两平行直线的距离处处相等性质,就可以将所求线段 平行移动到
端点在坐标轴上的线段
x
y
M
N
O
过 的直线方程
令
得
4、证明
由猜想的结果知道,分子应该是
这里如何消去
,而引入 ?
因为在直线 :
所以
所以
代入(1)得
意外收获:
两平行直线之间的距离公式:
两平行线 与 间的距离公式
公式的辨析:
(1)公式的结构特征:分子是将点的坐标代入直线方程一般式的左边得到的代数式加绝对值,分母是 ;
(2)公式的适用范围:1、该公式对于任何位置的点(包括直线上的点)及任意直线都适合。2、当 公式仍成立,但计算常用图形直接求解。
(3)公式时应注意的问题:使用点到直线距离公式时,应先将直线方程化为一般式。
(4) 用方程的观点理解公式:该公式是含有6个量的方程,知道其中5个量可以求第6个量。
释疑解惑
在推导公式的过程中,我们假定 ,那么如果 或 ,公式还成立吗?
(1)求点 到直线 的距离;
(2)求点 到直线 的距离。
结合图形,我们可以得到
y
x
0
例:已知P(-1,2) ,直线方程3x+4y-1=0 ,求P到直线的距离。
变式练习1、把直线改成y=10-2x呢?
变式练习2、求直线2x+y=10关于点P(0,1)对称的直线.
变式练习3、求过点P(-2,3),且与原点距离等于2的直线方程。
简单应用:
-------------点到直线的距离
一、创设情境
我们已学习了两点间的距离公式,本节课我们来研究:点到直线的距离。
已知假定在直角坐标系上,已知一个定点 ,和一条定直线l: ,如何求点到直线的距离?
l
x
y
o
Q
方法1、过P作直线Ax+By+C=0的垂线,先求出Q的坐标,再求出|PQ|.
方法2、(启发学生)采用从特殊到一般的思想方法。我们先从点P的特殊位置考虑。点的特殊位置(1)
(2) (3)
最后考虑一般情况(4)
情形1
x
y
M
N
Q
o
如何求OQ呢?
x
y
o
M
S
R
情形2
如何求 呢?
o
R
N
S
y
x
情形3
如何求 呢?
观察、归纳、猜想
我们能不能从这三种特殊情况中发现一般规律呢?
观察、类比前面三个公式,猜想出当点的坐标均不为0时,距离公式可能为
3、共同探讨
当任意一点不在坐标轴上时,如何利用前面的结论,求出P到的l距离呢?
能不能从X(或Y)轴上找一点,使它到l的距离等于 , 即能否将此距离转化为X(或Y)轴上一点到l的距离.
利用两平行直线的距离处处相等性质,就可以将所求线段 平行移动到
端点在坐标轴上的线段
x
y
M
N
O
过 的直线方程
令
得
4、证明
由猜想的结果知道,分子应该是
这里如何消去
,而引入 ?
因为在直线 :
所以
所以
代入(1)得
意外收获:
两平行直线之间的距离公式:
两平行线 与 间的距离公式
公式的辨析:
(1)公式的结构特征:分子是将点的坐标代入直线方程一般式的左边得到的代数式加绝对值,分母是 ;
(2)公式的适用范围:1、该公式对于任何位置的点(包括直线上的点)及任意直线都适合。2、当 公式仍成立,但计算常用图形直接求解。
(3)公式时应注意的问题:使用点到直线距离公式时,应先将直线方程化为一般式。
(4) 用方程的观点理解公式:该公式是含有6个量的方程,知道其中5个量可以求第6个量。
释疑解惑
在推导公式的过程中,我们假定 ,那么如果 或 ,公式还成立吗?
(1)求点 到直线 的距离;
(2)求点 到直线 的距离。
结合图形,我们可以得到
y
x
0
例:已知P(-1,2) ,直线方程3x+4y-1=0 ,求P到直线的距离。
变式练习1、把直线改成y=10-2x呢?
变式练习2、求直线2x+y=10关于点P(0,1)对称的直线.
变式练习3、求过点P(-2,3),且与原点距离等于2的直线方程。
简单应用:
