人教A版高中数学必修1第二章2.1.1 指数与指数幂的运算课件(16张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第二章2.1.1 指数与指数幂的运算课件(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 479.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 16:59:23 | ||
图片预览






文档简介
2020/12/27
2.1.1指数与指数幂的运算
第一课时
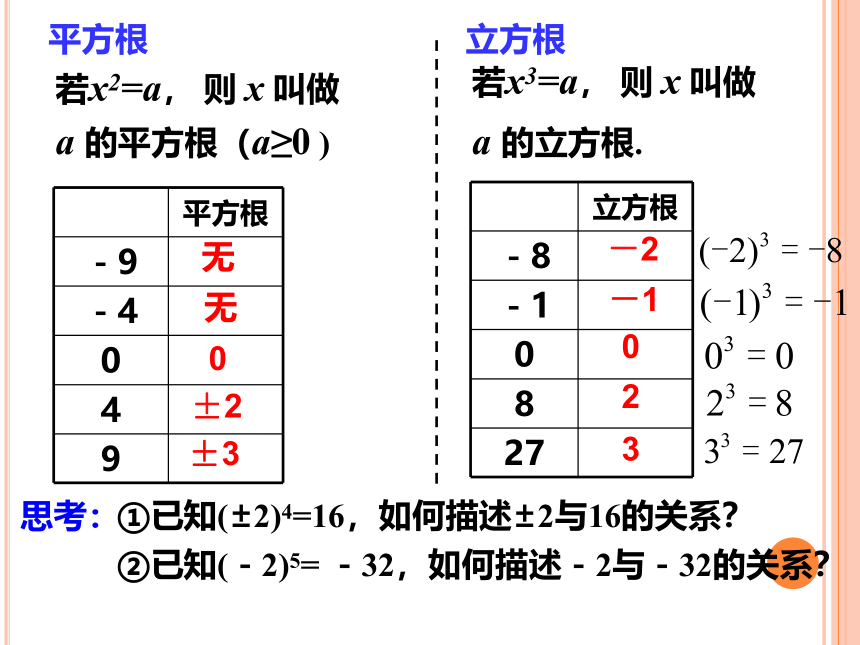
平方根
若x2=a, 则 x 叫做
立方根
若x3=a, 则 x 叫做
平方根
-9
-4
0
4
9
立方根
-8
-1
0
8
27
无
无
0
±2
±3
-2
-1
0
2
3
②已知(-2)5= -32,如何描述-2与-32的关系?
①已知(±2)4=16,如何描述±2与16的关系?
思考:
a 的平方根(a≥0 )
a 的立方根.
若xn=a,则x叫做a的n次方根,其中n>1且n∈N*
一、n次方根、根式的概念
(1)25的平方根是_______;
(2)27的三次方根是_____;
(3)-32的五次方根是____;
(4)16的四次方根是_____;
(5)a6的三次方根是_____;
(6)0的七次方根是______.
±5
3
-2
±2
0
a2
思考:一个数的n次方根有多少个?
①当n为奇数时, a的n次方根只有1个,用 表示
②当n为偶数时,
0的n次方根有1个,是0
负数没有偶次方根.
正数的n次方根有2个,
用 表示
(当n是奇数)
(当n是偶数,且a>0)
即:
式子 叫做根式, n 叫做根指数, a 叫做被开方数
一、n次方根、根式的概念
例1: 计算下列各式的值
① ;
③ ;
② ;
④ ;
⑤ ;
4
9
16
-1
-8
例题分析
公式1:
例2: 计算下列各式的值
例题分析
① ;
③ ;
② ;
④ ;
⑤ ;
公式2:
当n为奇数时:
当n为偶数时:
2
3
2
-3
1
例题分析
例3. 求下列各式的值
解:
尝试练习
今天的你努力了吗?
宝贝们,加油。。。
二、分数指数幂
1.复习初中时的整数指数幂,运算性质
2.观察以下式子,并总结出规律:(a > 0)
结论:当根式的被开方数的指数能被根指数整除时,根式可以表示为分数指数幂的形式.
探究
利用(1)的规律,你能表示下列式子吗?
类比
总结:当根式的被开方数的指数不能被根指数整除时,根式可以写成分数指数幂的形式.
探究
你能用方根的意义解释这些式子吗?
43的5次方根是
75的3次方根是
a2的3次方根是
a9的7次方根是
结果表明:方根与分数指数幂是相通的.
综上,我们得到正数的正分数指数幂的意义.
新课讲解
2、分数指数幂
规定正数的分数指数幂的意义为:
(1)正数的负分数指数幂的意义与负整数幂的意
义相同.即:
(2)规定:0的正分数指数幂等于0,
0的负分数指数幂无意义.
(3)运算性质仍然适用
例题分析
例3 .根式与分数指数幂的互化
课堂小结
1、两个定义:
2、两个公式:
①
当n为奇数时,
当n为偶数时,
②
3、根式和分数指数幂的互化
n次方根,根式
2.1.1指数与指数幂的运算
第一课时
平方根
若x2=a, 则 x 叫做
立方根
若x3=a, 则 x 叫做
平方根
-9
-4
0
4
9
立方根
-8
-1
0
8
27
无
无
0
±2
±3
-2
-1
0
2
3
②已知(-2)5= -32,如何描述-2与-32的关系?
①已知(±2)4=16,如何描述±2与16的关系?
思考:
a 的平方根(a≥0 )
a 的立方根.
若xn=a,则x叫做a的n次方根,其中n>1且n∈N*
一、n次方根、根式的概念
(1)25的平方根是_______;
(2)27的三次方根是_____;
(3)-32的五次方根是____;
(4)16的四次方根是_____;
(5)a6的三次方根是_____;
(6)0的七次方根是______.
±5
3
-2
±2
0
a2
思考:一个数的n次方根有多少个?
①当n为奇数时, a的n次方根只有1个,用 表示
②当n为偶数时,
0的n次方根有1个,是0
负数没有偶次方根.
正数的n次方根有2个,
用 表示
(当n是奇数)
(当n是偶数,且a>0)
即:
式子 叫做根式, n 叫做根指数, a 叫做被开方数
一、n次方根、根式的概念
例1: 计算下列各式的值
① ;
③ ;
② ;
④ ;
⑤ ;
4
9
16
-1
-8
例题分析
公式1:
例2: 计算下列各式的值
例题分析
① ;
③ ;
② ;
④ ;
⑤ ;
公式2:
当n为奇数时:
当n为偶数时:
2
3
2
-3
1
例题分析
例3. 求下列各式的值
解:
尝试练习
今天的你努力了吗?
宝贝们,加油。。。
二、分数指数幂
1.复习初中时的整数指数幂,运算性质
2.观察以下式子,并总结出规律:(a > 0)
结论:当根式的被开方数的指数能被根指数整除时,根式可以表示为分数指数幂的形式.
探究
利用(1)的规律,你能表示下列式子吗?
类比
总结:当根式的被开方数的指数不能被根指数整除时,根式可以写成分数指数幂的形式.
探究
你能用方根的意义解释这些式子吗?
43的5次方根是
75的3次方根是
a2的3次方根是
a9的7次方根是
结果表明:方根与分数指数幂是相通的.
综上,我们得到正数的正分数指数幂的意义.
新课讲解
2、分数指数幂
规定正数的分数指数幂的意义为:
(1)正数的负分数指数幂的意义与负整数幂的意
义相同.即:
(2)规定:0的正分数指数幂等于0,
0的负分数指数幂无意义.
(3)运算性质仍然适用
例题分析
例3 .根式与分数指数幂的互化
课堂小结
1、两个定义:
2、两个公式:
①
当n为奇数时,
当n为偶数时,
②
3、根式和分数指数幂的互化
n次方根,根式
