人教A版高中数学必修1第二章2.2.1对数与对数运算课件(20张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第二章2.2.1对数与对数运算课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 654.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览




文档简介
2.2.1对数与对数运算
高中数学人教A版必修一
第二章 基本初等函数(I)
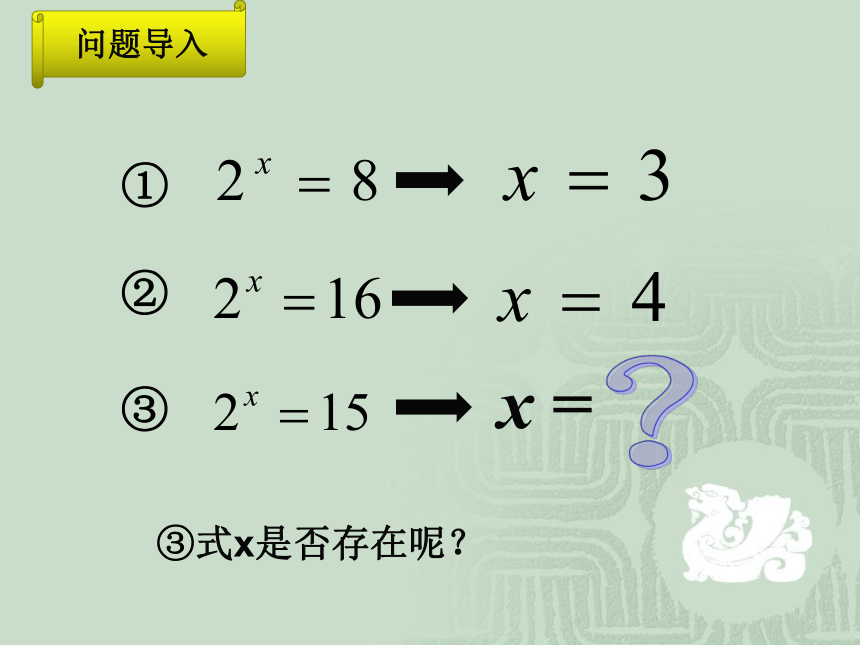
x =
③式x是否存在呢?
问题导入
①
③
②
?
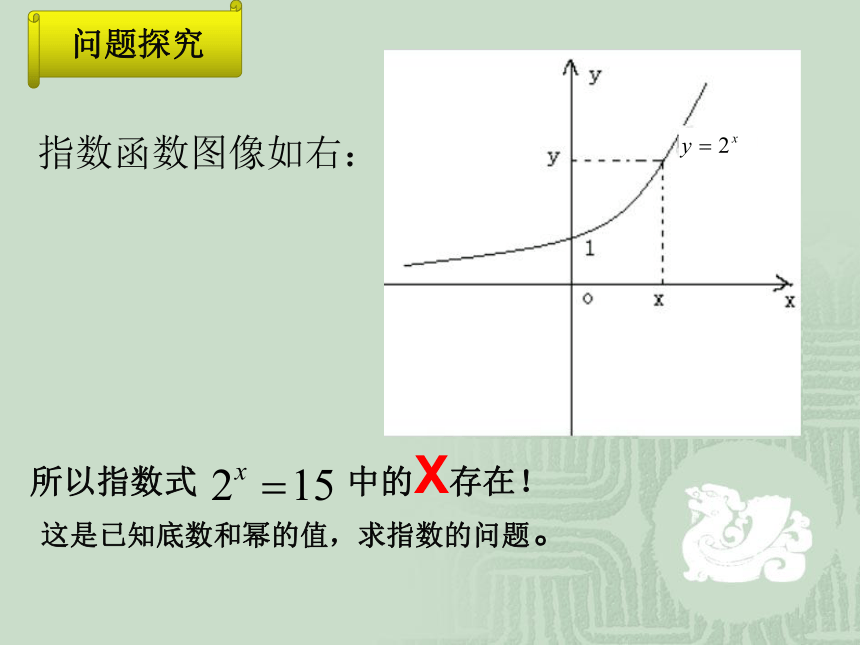
指数函数图像如右:
所以指数式 中的X存在!
问题探究
这是已知底数和幂的值,求指数的问题。
为了解决“已知底数和幂的值,求指数”这类问题,
引进对数
一般地,如果ax=N(a>0,且a≠1),
那么数x叫做以a为底N的对数(logarithm),
记作
其中a叫做对数的底数,N叫做真数。
对数定义
N
a
l
o
g
对数的写法
对数定义的剖析
问题1: 的含义是什么? 含义 ?
对数是一个数,对数者,指数也。
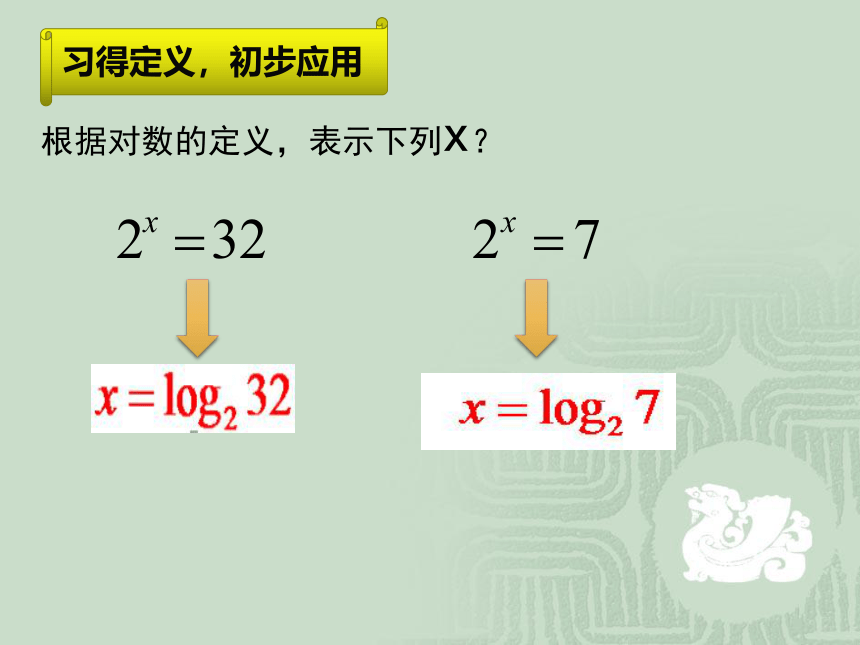
根据对数的定义,表示下列x?
习得定义,初步应用
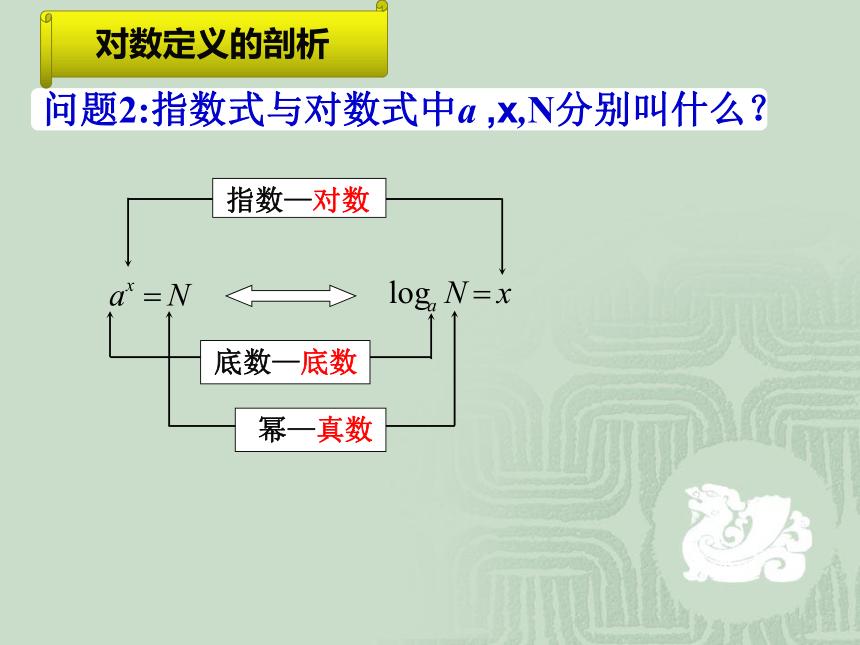
指数—对数
底数—底数
幂—真数
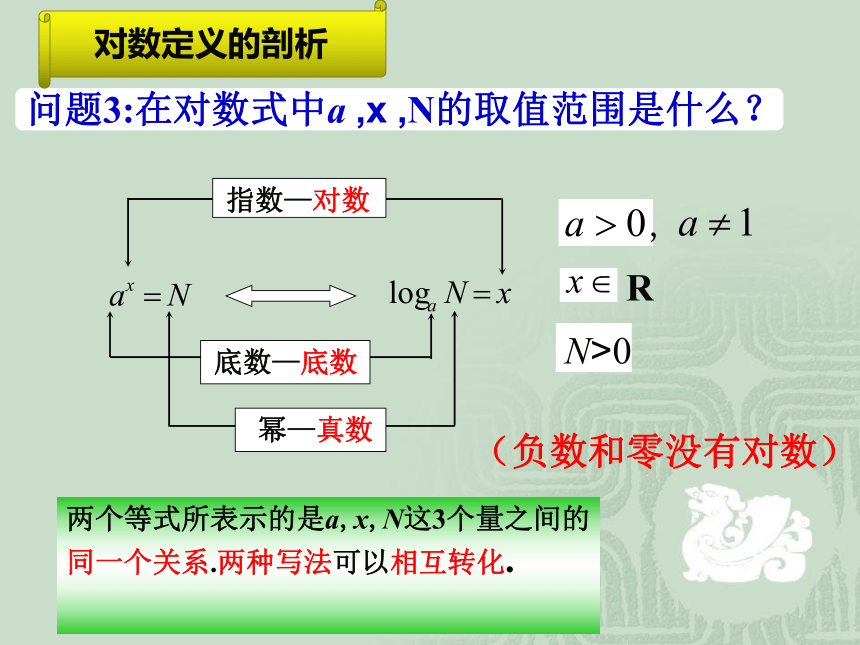
问题2:指数式与对数式中a ,x,N分别叫什么?
对数定义的剖析
指数—对数
底数—底数
幂—真数
问题3:在对数式中a ,x ,N的取值范围是什么?
N>0
R
,
(负数和零没有对数)
两个等式所表示的是a,x,N这3个量之间的同一个关系.两种写法可以相互转化.
对数定义的剖析
指数式与对数式互化
(1)
(2)
(3)
(4)
应用举例1
常用对数
以10为底的对数称为常用对数,即 简记为lgN
两种特殊的对数
自然对数
以e为底的对数称为自然对数,
把 简记为lnN
自然常数
两种特殊的对数
根据对数的定义,写出下列各对数的值:
应用探究
log31=
(6) lg10=
(1)
log33=
(2)
(4)
(5) ln1=
(4)
(3)
;
;
;
;
;
.
log0.50.5=
根据对数的定义,写出下列各对数的值:
应用探究
log31=
(6) lg10=
(1)
log33=
(2)
(4)
(5) ln1=
(4)
(3)
;
;
;
;
;
.
log0.50.5=
0
0
0
1
1
1
观察上述各式,进行适当分类,归纳出一般性结论.
=0
应用探究1
log31
(1)
(4)
■
=0
■
■
(5) ln1
=0
对任意a>0且a≠1,都有
( 1的对数为0 )
结论:
应用探究2
=1
=1
=1
(6) lg10
log33
(2)
■
■
(3) lne
■
对任意a>0且a≠1,都有
(底数的对数为1 )
结论:
求下列各式中x的值:
(1)
(2)
解:
(1)因为
所以
(2)因为
所以
于是
应用举例2
解:(1)
(4)
(3)
(2)
求下列各式的值
(1)
(4)
(3)
(2)
25
log
5
课堂练习
1.对数的定义
2.掌握指数式与对数式的互化
4.会用指数运算求简单的对数值
(a>0,a≠1)
3.对数的基本性质
关于对数的概念要注意以下几点
知识详解
高中数学人教A版必修一
第二章 基本初等函数(I)
x =
③式x是否存在呢?
问题导入
①
③
②
?
指数函数图像如右:
所以指数式 中的X存在!
问题探究
这是已知底数和幂的值,求指数的问题。
为了解决“已知底数和幂的值,求指数”这类问题,
引进对数
一般地,如果ax=N(a>0,且a≠1),
那么数x叫做以a为底N的对数(logarithm),
记作
其中a叫做对数的底数,N叫做真数。
对数定义
N
a
l
o
g
对数的写法
对数定义的剖析
问题1: 的含义是什么? 含义 ?
对数是一个数,对数者,指数也。
根据对数的定义,表示下列x?
习得定义,初步应用
指数—对数
底数—底数
幂—真数
问题2:指数式与对数式中a ,x,N分别叫什么?
对数定义的剖析
指数—对数
底数—底数
幂—真数
问题3:在对数式中a ,x ,N的取值范围是什么?
N>0
R
,
(负数和零没有对数)
两个等式所表示的是a,x,N这3个量之间的同一个关系.两种写法可以相互转化.
对数定义的剖析
指数式与对数式互化
(1)
(2)
(3)
(4)
应用举例1
常用对数
以10为底的对数称为常用对数,即 简记为lgN
两种特殊的对数
自然对数
以e为底的对数称为自然对数,
把 简记为lnN
自然常数
两种特殊的对数
根据对数的定义,写出下列各对数的值:
应用探究
log31=
(6) lg10=
(1)
log33=
(2)
(4)
(5) ln1=
(4)
(3)
;
;
;
;
;
.
log0.50.5=
根据对数的定义,写出下列各对数的值:
应用探究
log31=
(6) lg10=
(1)
log33=
(2)
(4)
(5) ln1=
(4)
(3)
;
;
;
;
;
.
log0.50.5=
0
0
0
1
1
1
观察上述各式,进行适当分类,归纳出一般性结论.
=0
应用探究1
log31
(1)
(4)
■
=0
■
■
(5) ln1
=0
对任意a>0且a≠1,都有
( 1的对数为0 )
结论:
应用探究2
=1
=1
=1
(6) lg10
log33
(2)
■
■
(3) lne
■
对任意a>0且a≠1,都有
(底数的对数为1 )
结论:
求下列各式中x的值:
(1)
(2)
解:
(1)因为
所以
(2)因为
所以
于是
应用举例2
解:(1)
(4)
(3)
(2)
求下列各式的值
(1)
(4)
(3)
(2)
25
log
5
课堂练习
1.对数的定义
2.掌握指数式与对数式的互化
4.会用指数运算求简单的对数值
(a>0,a≠1)
3.对数的基本性质
关于对数的概念要注意以下几点
知识详解
