人教A版高中数学必修1第二章2.1.2指数函数及其性质课件(17张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第二章2.1.2指数函数及其性质课件(17张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 30.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览





文档简介
指数函数及其性质
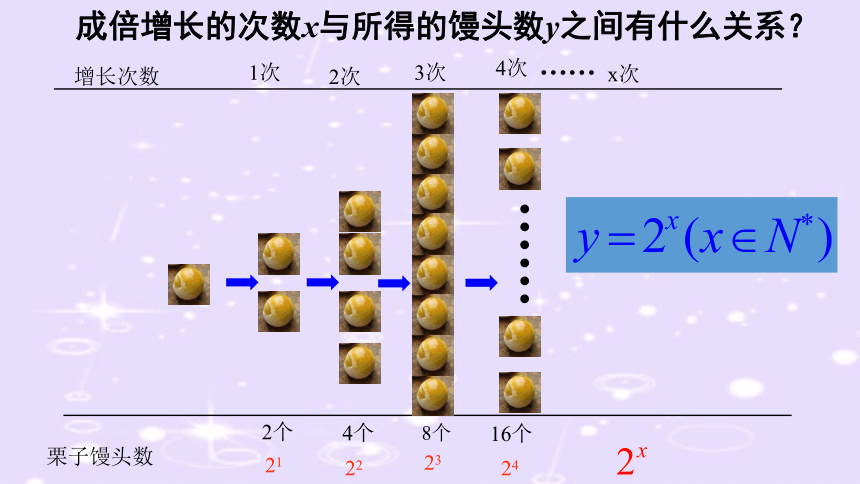
1小时之后是4096个
2小时之后是16777226个
再过15分钟之后就会超过100000000个
增长次数
栗子馒头数
1次
2次
3次
4次
x次
……
21
22
23
24
成倍增长的次数x与所得的馒头数y之间有什么关系?
……
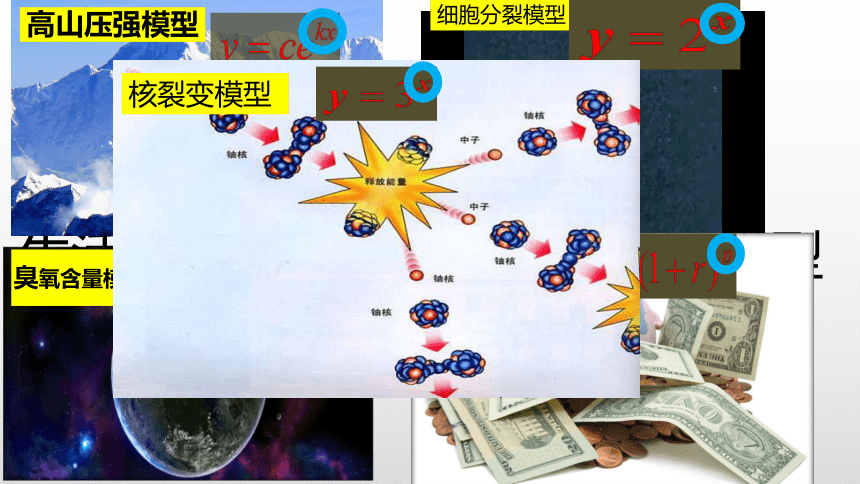
生活中我们有很多这样的函数模型
高山压强模型
臭氧含量模型
银行复利模型
细胞分裂模型
核裂变模型
函数 叫做指数函
数(exponential function),其中x是自变量,函数
的定义域是R.
指数函数
为什么要规定
的定义
底数是常数(大于0且不等于1)
指数为自变量
系数为1
y=1 · ax
再探究,再认识!
找找看,谁是指数函数?
试一试
课本P55页,填表
x
y
O
y
x
O
x
-3
-2
-1
0
1
2
3
x
-3
-2
-1
0
1
2
3
定义域
值域
单调性
奇偶性
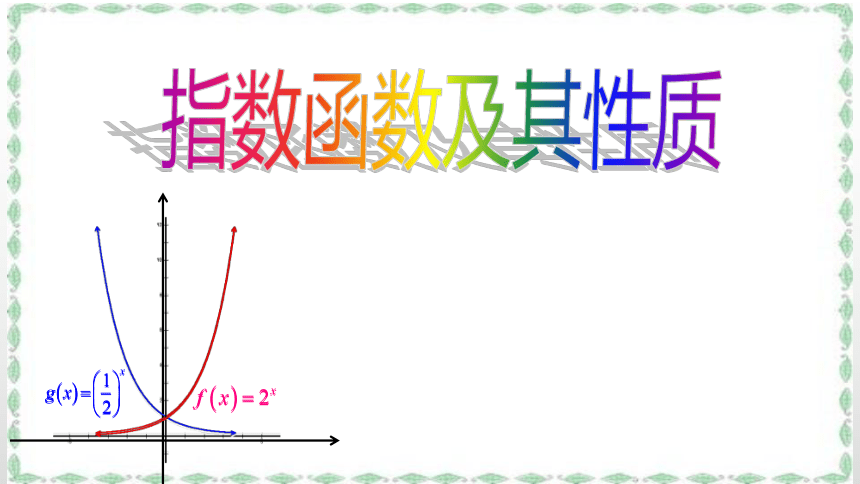
两个函数图象关于y 轴对称
两个函数图象都过点(0,1)
图
象
性
质
x
y
o
1
x
y
o
1
R
( 0 , + ∞)
过定点 ( 0 , 1 ),即x=0时,y=1
当x>0时,y>1
当x<0时,0<y<1
当x>0时, 0<y<1当x<0时, y>1
在R上是增函数
在R上是减函数
(1)定义域
(2)值域
(3)定点
(5)函数值的分布情况
(4)单调性
指数函数的图象和性质
a > 1
0 < a < 1
“提”
“捺”
课堂小结:
?一个函数
?两个图象
2.1.2 指数函数及其性质
例题精讲
例1:下列函数中,哪些是指数函数?
我是
我还不是
我不是
我也不是
你答对了吗?
2.1.2 指数函数及其性质
课堂练习
1、下列函数中,哪些是指数函数?
2、若函数y=(a2-3a+3)ax是指数函数,求a的值.
1小时之后是4096个
2小时之后是16777226个
再过15分钟之后就会超过100000000个
增长次数
栗子馒头数
1次
2次
3次
4次
x次
……
21
22
23
24
成倍增长的次数x与所得的馒头数y之间有什么关系?
……
生活中我们有很多这样的函数模型
高山压强模型
臭氧含量模型
银行复利模型
细胞分裂模型
核裂变模型
函数 叫做指数函
数(exponential function),其中x是自变量,函数
的定义域是R.
指数函数
为什么要规定
的定义
底数是常数(大于0且不等于1)
指数为自变量
系数为1
y=1 · ax
再探究,再认识!
找找看,谁是指数函数?
试一试
课本P55页,填表
x
y
O
y
x
O
x
-3
-2
-1
0
1
2
3
x
-3
-2
-1
0
1
2
3
定义域
值域
单调性
奇偶性
两个函数图象关于y 轴对称
两个函数图象都过点(0,1)
图
象
性
质
x
y
o
1
x
y
o
1
R
( 0 , + ∞)
过定点 ( 0 , 1 ),即x=0时,y=1
当x>0时,y>1
当x<0时,0<y<1
当x>0时, 0<y<1当x<0时, y>1
在R上是增函数
在R上是减函数
(1)定义域
(2)值域
(3)定点
(5)函数值的分布情况
(4)单调性
指数函数的图象和性质
a > 1
0 < a < 1
“提”
“捺”
课堂小结:
?一个函数
?两个图象
2.1.2 指数函数及其性质
例题精讲
例1:下列函数中,哪些是指数函数?
我是
我还不是
我不是
我也不是
你答对了吗?
2.1.2 指数函数及其性质
课堂练习
1、下列函数中,哪些是指数函数?
2、若函数y=(a2-3a+3)ax是指数函数,求a的值.
