人教A版高中数学必修1第二章2.2.2 对数函数及其性质课件(23张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第二章2.2.2 对数函数及其性质课件(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 733.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览






文档简介
第2章
基本初等函数(Ⅰ)
2.2.2 对数函数及其性质
温故知新
回顾研究指数函数的过程:
前面我们已经学习过 指数式
对数式
对数函数
1.定义
2.画图
3.性质
指数函数
我们把函数 叫做指数函数
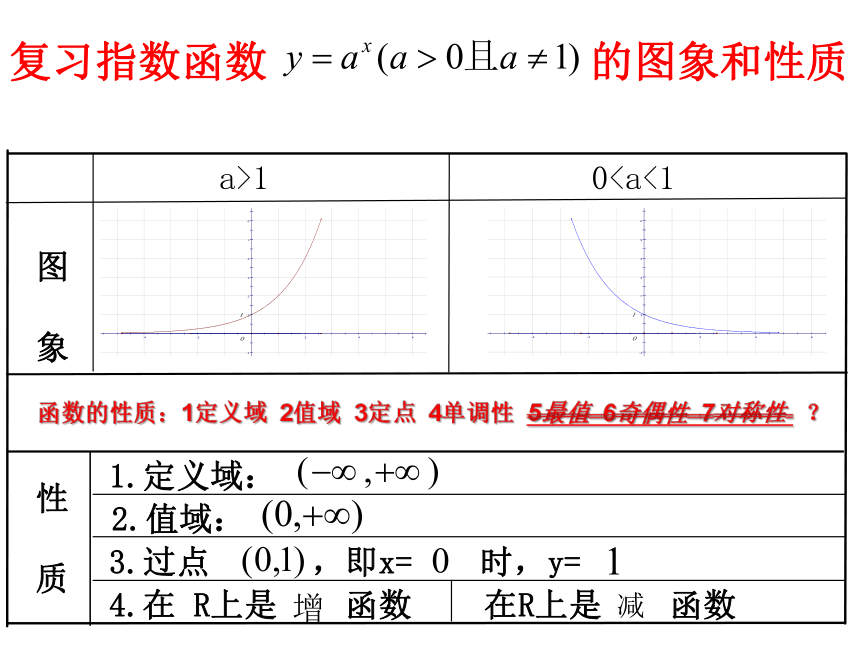
在R上是 函数
4.在 R上是 函数
3.过点 ,即x= 时,y=
2.值域:
1.定义域:
性
质
图
象
0 a>1
复习指数函数 的图象和性质
函数的性质:1定义域 2值域 3定点 4单调性 5最值 6奇偶性 7对称性 ?
本节课的学习预告:
1.对数函数的定义
2.画出对数函数的图象
3.对数函数性质
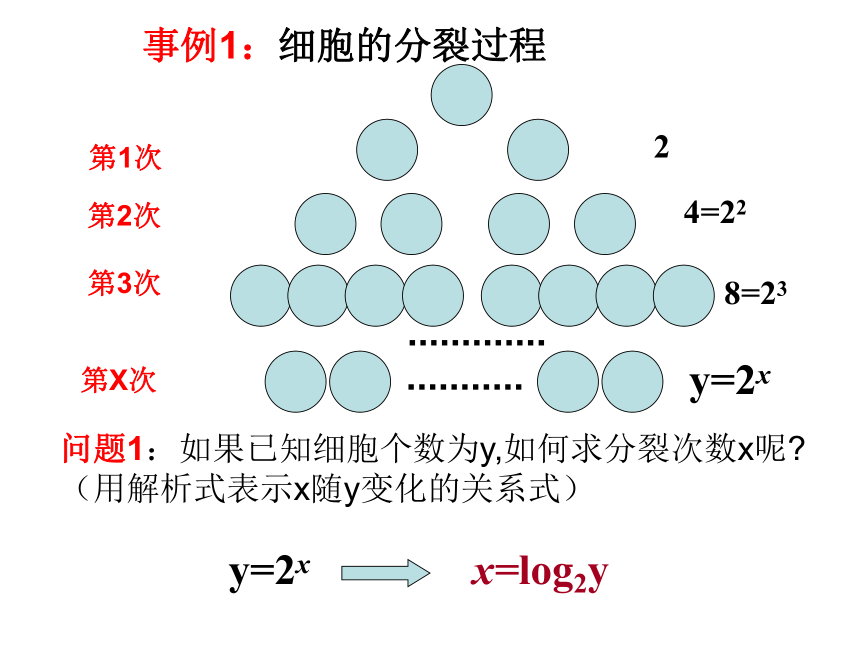
事例1:细胞的分裂过程
第1次
第2次
第X次
第3次
y=2x
2
4=22
8=23
问题1:如果已知细胞个数为y,如何求分裂次数x呢?(用解析式表示x随y变化的关系式)
x=log2y
y=2x
-3 -2 -1 O 1 2 3 x
8 7 6 5 4 3 2 1
y
y = 2 x
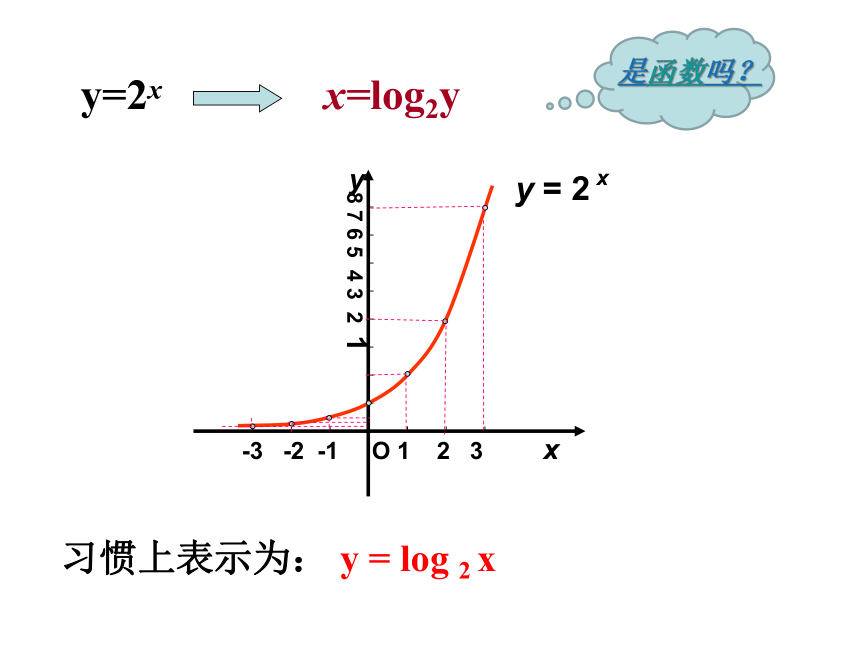
x=log2y
y=2x
习惯上表示为: y = log 2 x
是函数吗?
一般地,函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,
函数的定义域是( 0 , +∞).
对数函数的定义:
注意:1)对数函数定义是形式定义:
2)对数函数对底数的限制条件:
想一想?
为什么函数的定义域是(0,+∞)?
即真数大于0?
1
1
1
辨析:
下列函数是否为对数函数
×
×
×
×
例1求下列函数的定义域:
(1)
讲解范例
(2)
课堂练习: 求下列函数的定义域:
(1)
(2)
(3)
)
,
1
(
)
1
,
0
(
+?
∪
二、对数函数的图象和性质:
在同一个直角坐标系里,画出下列函数的图象:
定义域是 (0,+∞)
…
…
…
…
-2
-1
1
0
2
1
4
2
…
…
…
…
-2
-1
1
0
3
1
9
2
1 2 3 4 5 6 7 8 9
x
O
1
2
3
-2
-1
-3
y
1 2 3 4 5 6 7 8 9
x
O
1
2
3
-2
-1
-3
y
…
…
…
…
2
1
1
0
2
-1
4
-2
…
…
…
…
2
1
1
0
3
-1
9
-2
请归纳这些
函数图象的特征
图
象
对数函数的性质:
x
y
0
1
x
y
0
1
定义域: (0,+∞)
值 域:R
过定点:(1,0),
在 (0,+∞)上是增函数
在 (0,+∞)上是减函数
图象位于y轴右侧
经过(1,0)点
自左往右呈上升趋势
自左往右呈下降趋势
图象向上、向下无限延伸
图象特征
函数性质
例2.比较下列各组数中两个值的大小:
解: (1)考察对数函数
,它在
上是增函数
如果改成以0.3为底?
如果改成以 为底?
(0,+∞)
解:
(一)同底数比较大小
1.当底数确定时,
(二)若底数、真数都不相同,
归纳:两个对数比较大小
则常借助1、0等中间量进行比较。
则可由函数的单调性直接进行判断;
2.当底数不确定时,
应对底数进行分类讨论。
课堂练习:
比较下列各题中两个值的大小:
<
>
<
<
练习:
已知下列不等式,比较正数m,n 的大小:
(1)
(2)
(3)
(1)
(2)
(3)
解:
图
象
课堂小结:
x
y
0
1
x
y
0
1
定义域: (0,+∞)
值 域:R
过定点:(1,0),
在 (0,+∞)上是增函数
在 (0,+∞)上是减函数
图象位于y轴右侧
经过(1,0)点
自左往右呈上升趋势
自左往右呈下降趋势
图象向上、向下无限延伸
图象特征
函数性质
(三)拓展探究题
1
0
如图,已知函数y=logax,y=logbx,y=logcx,
y=logdx的图象分别是曲线C1,C2,C3,C4,试判断0,1,a,b,c,d的大小关系,并用“<”连接起来.
0 设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f: A→B为从集合A到集合B的一个函数,
记作 y=f(x),x∈A
函数的定义
例题:
函数定义
定义域
单调性
辨析函数是否为对数函数
对应例题
求函数的定义域
教材71页 例7
教材73页 练习2
“比大小”
教材72页 例8
教材73页 练习3
知识点
函数性质
基本初等函数(Ⅰ)
2.2.2 对数函数及其性质
温故知新
回顾研究指数函数的过程:
前面我们已经学习过 指数式
对数式
对数函数
1.定义
2.画图
3.性质
指数函数
我们把函数 叫做指数函数
在R上是 函数
4.在 R上是 函数
3.过点 ,即x= 时,y=
2.值域:
1.定义域:
性
质
图
象
0
复习指数函数 的图象和性质
函数的性质:1定义域 2值域 3定点 4单调性 5最值 6奇偶性 7对称性 ?
本节课的学习预告:
1.对数函数的定义
2.画出对数函数的图象
3.对数函数性质
事例1:细胞的分裂过程
第1次
第2次
第X次
第3次
y=2x
2
4=22
8=23
问题1:如果已知细胞个数为y,如何求分裂次数x呢?(用解析式表示x随y变化的关系式)
x=log2y
y=2x
-3 -2 -1 O 1 2 3 x
8 7 6 5 4 3 2 1
y
y = 2 x
x=log2y
y=2x
习惯上表示为: y = log 2 x
是函数吗?
一般地,函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,
函数的定义域是( 0 , +∞).
对数函数的定义:
注意:1)对数函数定义是形式定义:
2)对数函数对底数的限制条件:
想一想?
为什么函数的定义域是(0,+∞)?
即真数大于0?
1
1
1
辨析:
下列函数是否为对数函数
×
×
×
×
例1求下列函数的定义域:
(1)
讲解范例
(2)
课堂练习: 求下列函数的定义域:
(1)
(2)
(3)
)
,
1
(
)
1
,
0
(
+?
∪
二、对数函数的图象和性质:
在同一个直角坐标系里,画出下列函数的图象:
定义域是 (0,+∞)
…
…
…
…
-2
-1
1
0
2
1
4
2
…
…
…
…
-2
-1
1
0
3
1
9
2
1 2 3 4 5 6 7 8 9
x
O
1
2
3
-2
-1
-3
y
1 2 3 4 5 6 7 8 9
x
O
1
2
3
-2
-1
-3
y
…
…
…
…
2
1
1
0
2
-1
4
-2
…
…
…
…
2
1
1
0
3
-1
9
-2
请归纳这些
函数图象的特征
图
象
对数函数的性质:
x
y
0
1
x
y
0
1
定义域: (0,+∞)
值 域:R
过定点:(1,0),
在 (0,+∞)上是增函数
在 (0,+∞)上是减函数
图象位于y轴右侧
经过(1,0)点
自左往右呈上升趋势
自左往右呈下降趋势
图象向上、向下无限延伸
图象特征
函数性质
例2.比较下列各组数中两个值的大小:
解: (1)考察对数函数
,它在
上是增函数
如果改成以0.3为底?
如果改成以 为底?
(0,+∞)
解:
(一)同底数比较大小
1.当底数确定时,
(二)若底数、真数都不相同,
归纳:两个对数比较大小
则常借助1、0等中间量进行比较。
则可由函数的单调性直接进行判断;
2.当底数不确定时,
应对底数进行分类讨论。
课堂练习:
比较下列各题中两个值的大小:
<
>
<
<
练习:
已知下列不等式,比较正数m,n 的大小:
(1)
(2)
(3)
(1)
(2)
(3)
解:
图
象
课堂小结:
x
y
0
1
x
y
0
1
定义域: (0,+∞)
值 域:R
过定点:(1,0),
在 (0,+∞)上是增函数
在 (0,+∞)上是减函数
图象位于y轴右侧
经过(1,0)点
自左往右呈上升趋势
自左往右呈下降趋势
图象向上、向下无限延伸
图象特征
函数性质
(三)拓展探究题
1
0
如图,已知函数y=logax,y=logbx,y=logcx,
y=logdx的图象分别是曲线C1,C2,C3,C4,试判断0,1,a,b,c,d的大小关系,并用“<”连接起来.
0
记作 y=f(x),x∈A
函数的定义
例题:
函数定义
定义域
单调性
辨析函数是否为对数函数
对应例题
求函数的定义域
教材71页 例7
教材73页 练习2
“比大小”
教材72页 例8
教材73页 练习3
知识点
函数性质
