人教A版高中数学必修1第二章2.2.2对数函数及其性质课件 (1)(40张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第二章2.2.2对数函数及其性质课件 (1)(40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1008.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览





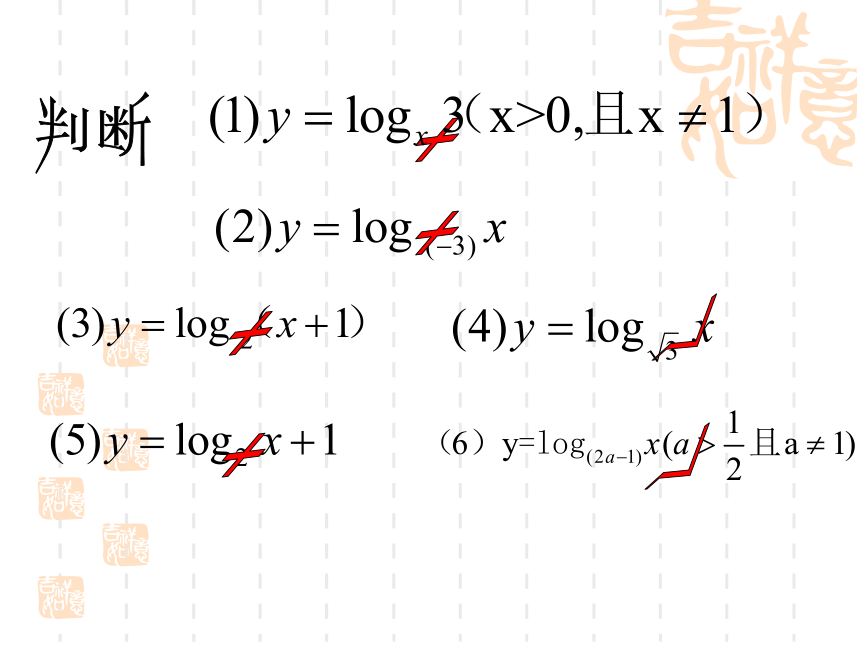



文档简介
§2.2.2 对数函数及其性质
教学目标
理解对数函数的概念,掌握对数函数的性质,通过对对数函数的学习,渗透数形结合,分类讨论,转化等数学思想。
能根据对数函数的图象,画出含有对数式的函数的图象。
重点难点
重点:对数函数的概念、图像和性质;
难点:对数函数的图像和性质与其底数的关系。
对数函数及其性质
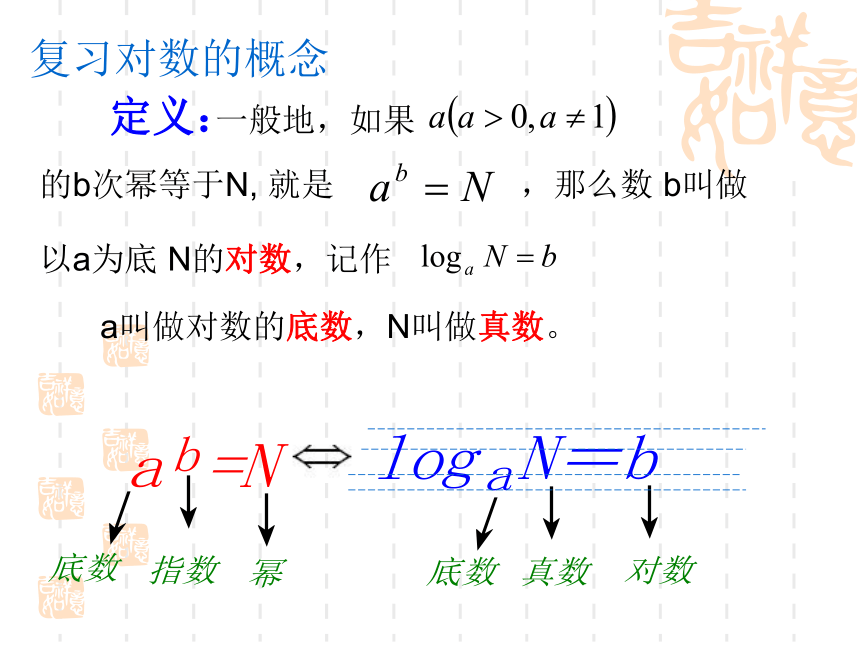
一般地,如果
的b次幂等于N, 就是
,那么数 b叫做
以a为底 N的对数,记作
a叫做对数的底数,N叫做真数。
复习对数的概念
定义:
由前面的学习我们知道:如果有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· ,1个这样的细胞分裂x次会得到多少个细胞?
如果知道了细胞的个数y,如何确定分裂的次数x呢?
由对数式与指数式的互化可知:
对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即
这就是本节课要学习的:
对数函数
一般地,函数y = loga x (a>0,且a≠ 1)叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)
一引导探究,形成概念
判断
√
×
×
×
×
√
①、对数的形式
②、底数大于0 且不等于1的常数;
③、x是自变量,定义域( 0 , +∞) 。
对数函数有哪些特征?
怎样判断一个函数是对数函数?
想一想
二.对数函数的图象:
1.描点画图
在同一平面直角坐标系中做出
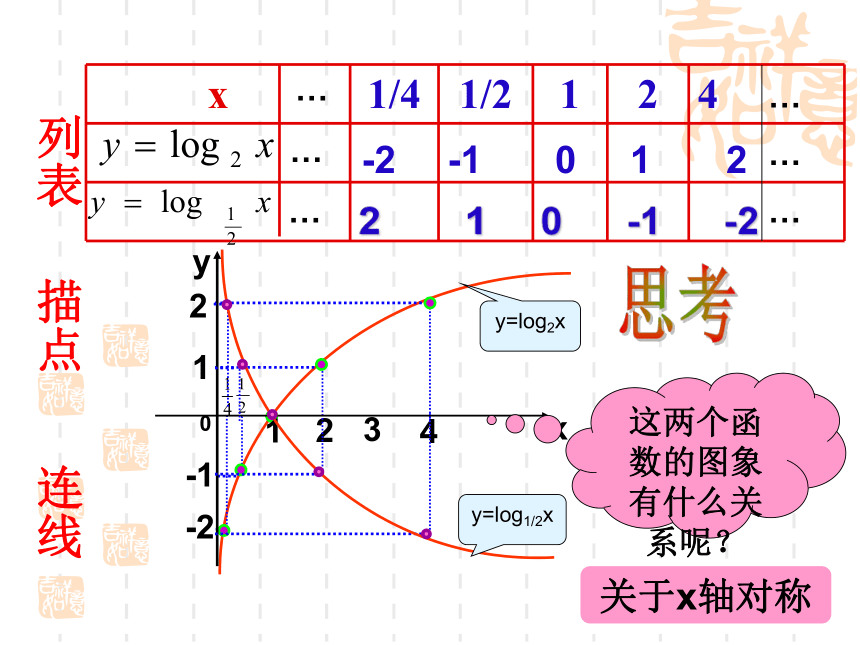
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
y=log1/2x
y=log2x
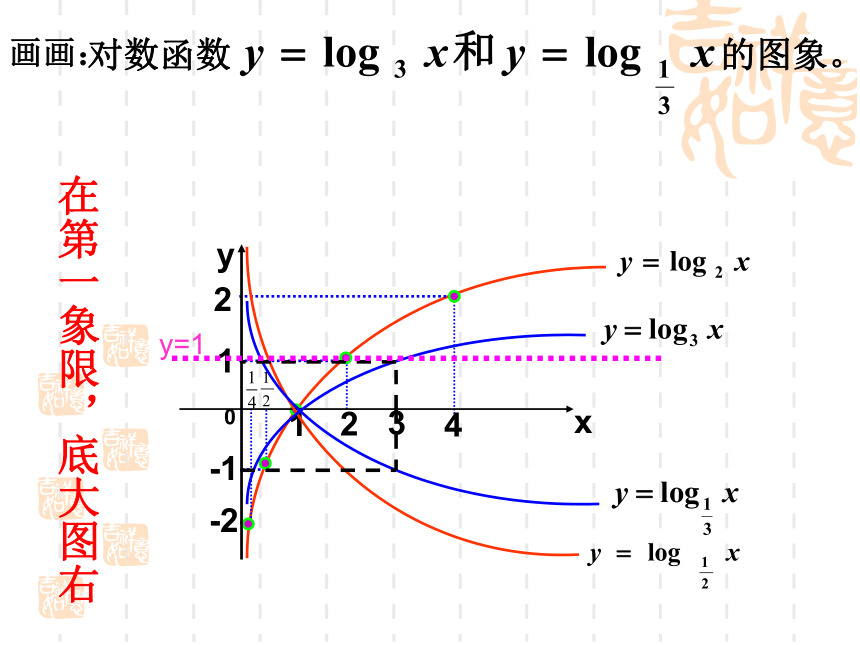
对数函数 的图象。
画画:
2
1
-1
-2
1
2
4
0
y
x
3
在第一象限,底大图右
y=1
思考:对数函数:y = loga x (a>0,且a≠ 1) 图象随着a的取值变化图象如何变化?有规律吗?
返回
再来一遍
对数函数及其性质
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
图 象 性 质
a > 1 0 < a < 1
定义域 :
值 域 :
过定点
在(0,+∞)上是
在(0,+∞)上是
对数函数的图像与性质
当x>1时, 当x=1时, 当0( 0,+∞)
R
(1 ,0),
即当x =1时,y=0
增函数
减函数
y>0
y=0
y<0
当x>1时, 当x=1时, 当0y<0
y=0
y>0
例1:求下列函数的定义域:
(1) y=logax2 (2) y=loga(4-x)
解:
(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为
?-???? ? (0,+??
(2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为
(-??4)
习题讲解
例1中求定义域时应注意:
对数的真数大于0,底数大于0且不等于1;
使式子符合实际背景;
对含有字母的式子要注意分类讨论。
课堂训练
1、已知某对数函数的图像过点(4,2),则该函数的解析式为 。
2、函数 的图象恒过定点 。
3、求下列函数的定义域
(1) (2)
(3) (4)
(0,-2)
对数函数及其性质
小结
(1)对数函数的概念
(2)对数函数的图象与性质
(3)数形结合与转化的数学思想
正式作业:课本P74 第7题、P82 第3、4、5题;导学案:P103-P105
对数函数及其性质
谢谢
谢谢
教学目标
理解对数函数的概念,掌握对数函数的性质,通过对对数函数的学习,渗透数形结合,分类讨论,转化等数学思想。
能根据对数函数的图象,画出含有对数式的函数的图象。
重点难点
重点:对数函数的概念、图像和性质;
难点:对数函数的图像和性质与其底数的关系。
对数函数及其性质
一般地,如果
的b次幂等于N, 就是
,那么数 b叫做
以a为底 N的对数,记作
a叫做对数的底数,N叫做真数。
复习对数的概念
定义:
由前面的学习我们知道:如果有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· ,1个这样的细胞分裂x次会得到多少个细胞?
如果知道了细胞的个数y,如何确定分裂的次数x呢?
由对数式与指数式的互化可知:
对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即
这就是本节课要学习的:
对数函数
一般地,函数y = loga x (a>0,且a≠ 1)叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)
一引导探究,形成概念
判断
√
×
×
×
×
√
①、对数的形式
②、底数大于0 且不等于1的常数;
③、x是自变量,定义域( 0 , +∞) 。
对数函数有哪些特征?
怎样判断一个函数是对数函数?
想一想
二.对数函数的图象:
1.描点画图
在同一平面直角坐标系中做出
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
y=log1/2x
y=log2x
对数函数 的图象。
画画:
2
1
-1
-2
1
2
4
0
y
x
3
在第一象限,底大图右
y=1
思考:对数函数:y = loga x (a>0,且a≠ 1) 图象随着a的取值变化图象如何变化?有规律吗?
返回
再来一遍
对数函数及其性质
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
图 象 性 质
a > 1 0 < a < 1
定义域 :
值 域 :
过定点
在(0,+∞)上是
在(0,+∞)上是
对数函数的图像与性质
当x>1时, 当x=1时, 当0
R
(1 ,0),
即当x =1时,y=0
增函数
减函数
y>0
y=0
y<0
当x>1时, 当x=1时, 当0
y=0
y>0
例1:求下列函数的定义域:
(1) y=logax2 (2) y=loga(4-x)
解:
(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为
?-???? ? (0,+??
(2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为
(-??4)
习题讲解
例1中求定义域时应注意:
对数的真数大于0,底数大于0且不等于1;
使式子符合实际背景;
对含有字母的式子要注意分类讨论。
课堂训练
1、已知某对数函数的图像过点(4,2),则该函数的解析式为 。
2、函数 的图象恒过定点 。
3、求下列函数的定义域
(1) (2)
(3) (4)
(0,-2)
对数函数及其性质
小结
(1)对数函数的概念
(2)对数函数的图象与性质
(3)数形结合与转化的数学思想
正式作业:课本P74 第7题、P82 第3、4、5题;导学案:P103-P105
对数函数及其性质
谢谢
谢谢
