人教A版高中数学必修1第二章2.2.2对数函数及其性质课件(26张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第二章2.2.2对数函数及其性质课件(26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 545.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 17:16:00 | ||
图片预览






文档简介
§2.2.2 对数函数及其性质
复 习
1、指数、对数的互化关系:
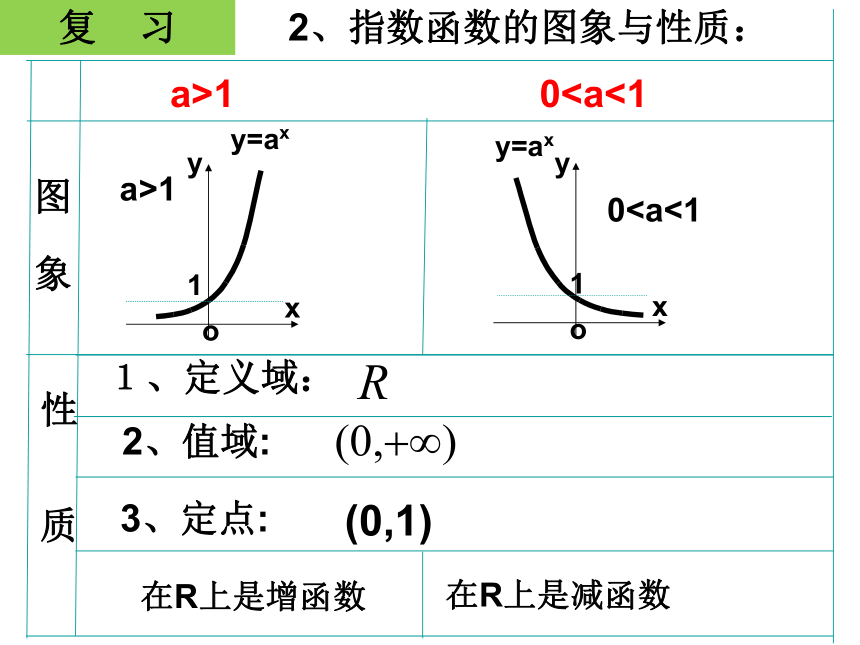
2、指数函数的图象与性质:
a>1
0图 象
性 质
1、定义域:
2、值域:
x
y
o
1
a>1
y=ax
在R上是增函数
在R上是减函数
x
y
o
1
0y=ax
3、定点:
(0,1)
复 习
2、指数函数的图象与性质:
问题2:
1
2
4
y=2x
……
y
x=?
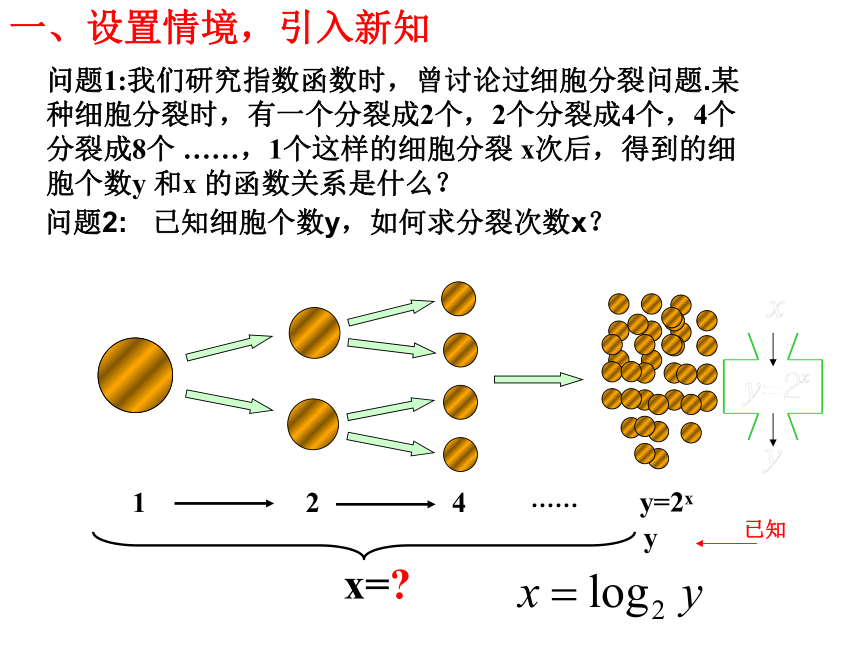
一、设置情境,引入新知
已知
问题1:我们研究指数函数时,曾讨论过细胞分裂问题.某种细胞分裂时,有一个分裂成2个,2个分裂成4个,4个分裂成8个 ……,1个这样的细胞分裂 x次后,得到的细胞个数y 和x 的函数关系是什么?
已知细胞个数y,如何求分裂次数x?
一般地,函数y = loga x(a>0,且a≠1)
叫做对数函数.其中 x是自变量.
函数的定义域是(0,+∞).
(一)引入新知
注意:
1、对数函数的定义:
二、合作交流,探索新知
(1)对数符号前面的系数为1;
(2)底数是大于零且不等于1的常数;
(3)真数是x的形式。
思考:定义中为什么要求a>0,且a≠1,x>0呢?
小试牛刀
以下函数是对数函数的是 ( )
A y=2log5x B y=log(a-1)x
C y=log5x D y=ln(x-1)
c
注意:
对数函数的定义与指数函数类似,都是形式定义,
注意辨别。
(二)探究图象和性质:
1、分组用描点法画出对数函数
的图象。
作图步骤: ①列表,
②描点,
③连接。
X
…
1
2
4
…
y=log2x
…
…
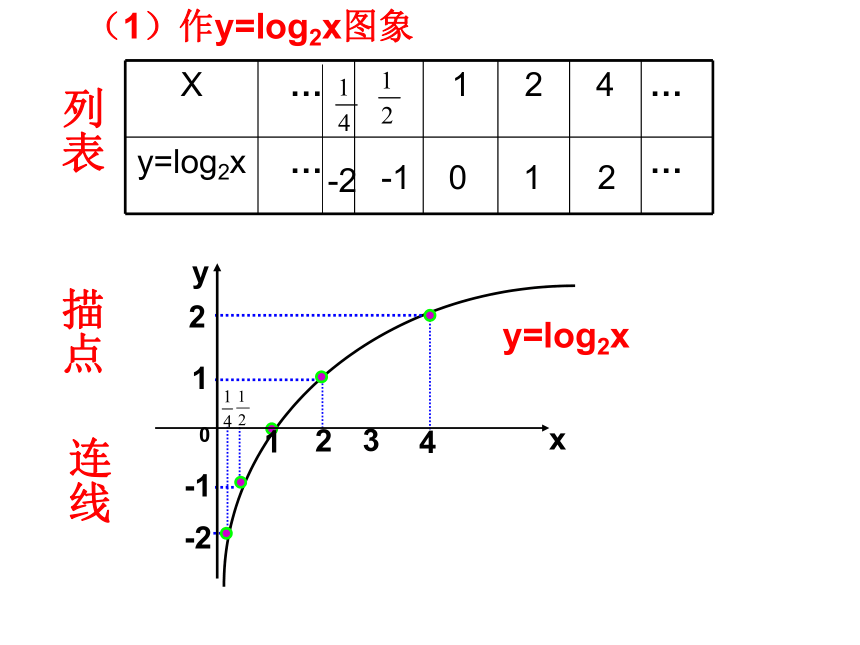
列表
描点
(1)作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
-2
-1
0
1
2
y=log2x
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
(2)作 的图象
y=log2x
思考:
刚才利用描点法作出了 和 的图象.还有其他方法可以作出它们的 图象吗?
y=log2x
图象特征
函数性质
图象位于y轴___________
图象向上、向下_______
自左向右看图象_______
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
探索发现:认真观察函数y=log2x和
的图象填写下表
图象特征
函数性质
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
右方
无限延伸
逐渐上升
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
图象位于y轴___________
图象向上、向下_______
自左向右看图象_______
图象特征
函数性质
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
右方
无限延伸
逐渐下降
图象位于y轴___________
图象向上、向下_______
自左向右看图象_______
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
探索发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
2
1
-1
-2
1
2
4
0
y
x
3
(3)再分别选取底数为 和 ,在同一平面直角坐标系内分组作出相应对数函数的图象.观察图象,你能发现它们有哪些共同特征吗?
图 象 性 质
a > 1 0 < a < 1
定义域 : ( 0,+∞)
值 域 : R
过定点(1 ,0), 即当x =1时,y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
y
x
0
y
x
0
(1,0)
(1,0)
对数函数y=logax (a>0,且a≠1)的图象与性质
当x>1时,y>0 当x=1时,y=0 当0当x>1时,y<0 当x=1时,y=0 当00
2、总结性质
练一练
分别画出下列函数的图象。(示意图)
(1)
(2)
例1 求下列函数的定义域:
(1)
(2)
(三)
解 :
解 :
由
得
∴函数
的定义域是
由
得
∴函数
的定义域是
由具体函数式求定义域,考虑以下几个方面:
(1)分母不等于0;
(2)偶次方根被开方数非负;
(3)零指数幂底数不为0;
(4)对数式考虑真数大于0;
(5)实际问题要有实际意义.
【提升总结】
我练练我掌握
1. 求下列函数的定义域:
(3)
(4)
(1)
( 2 )
解:(1){x|x<1}
(2) {x|x>0且x≠1}
(3){x|x< }
(4) {x|x≥1}
当堂检测
3.求下列函数的定义域:
2、分别画出下列函数的图象。(示意图)
(1)
(2)
(2)
(1)
1、判断下列函数是否为对数函数。
(1)y =2 loga x (a>0,且a≠ 1 )
(2)y = loga x2 (a>0,且a≠ 1 )
通过本节的学习,说出你的收获。
数形结合
对数函数
图 象
性 质
概 念
课堂小结
(1) 类比记忆指数函数和对数函数。
(2)看见函数式想图像,结合图像记性质。
课后作业
必做题
课本 练习2、
课本 习题2.2 A 组7、
选做题
课本 习题2.2 B 组2
课后能力提升:根据如图所示的四个对数函 数图象,比较a, b, c, d的大小。
x
y
1
祝同学们学习进步!
复 习
1、指数、对数的互化关系:
2、指数函数的图象与性质:
a>1
0
性 质
1、定义域:
2、值域:
x
y
o
1
a>1
y=ax
在R上是增函数
在R上是减函数
x
y
o
1
0
3、定点:
(0,1)
复 习
2、指数函数的图象与性质:
问题2:
1
2
4
y=2x
……
y
x=?
一、设置情境,引入新知
已知
问题1:我们研究指数函数时,曾讨论过细胞分裂问题.某种细胞分裂时,有一个分裂成2个,2个分裂成4个,4个分裂成8个 ……,1个这样的细胞分裂 x次后,得到的细胞个数y 和x 的函数关系是什么?
已知细胞个数y,如何求分裂次数x?
一般地,函数y = loga x(a>0,且a≠1)
叫做对数函数.其中 x是自变量.
函数的定义域是(0,+∞).
(一)引入新知
注意:
1、对数函数的定义:
二、合作交流,探索新知
(1)对数符号前面的系数为1;
(2)底数是大于零且不等于1的常数;
(3)真数是x的形式。
思考:定义中为什么要求a>0,且a≠1,x>0呢?
小试牛刀
以下函数是对数函数的是 ( )
A y=2log5x B y=log(a-1)x
C y=log5x D y=ln(x-1)
c
注意:
对数函数的定义与指数函数类似,都是形式定义,
注意辨别。
(二)探究图象和性质:
1、分组用描点法画出对数函数
的图象。
作图步骤: ①列表,
②描点,
③连接。
X
…
1
2
4
…
y=log2x
…
…
列表
描点
(1)作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
-2
-1
0
1
2
y=log2x
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
(2)作 的图象
y=log2x
思考:
刚才利用描点法作出了 和 的图象.还有其他方法可以作出它们的 图象吗?
y=log2x
图象特征
函数性质
图象位于y轴___________
图象向上、向下_______
自左向右看图象_______
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
探索发现:认真观察函数y=log2x和
的图象填写下表
图象特征
函数性质
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
右方
无限延伸
逐渐上升
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
图象位于y轴___________
图象向上、向下_______
自左向右看图象_______
图象特征
函数性质
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
右方
无限延伸
逐渐下降
图象位于y轴___________
图象向上、向下_______
自左向右看图象_______
探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质
探索发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
2
1
-1
-2
1
2
4
0
y
x
3
(3)再分别选取底数为 和 ,在同一平面直角坐标系内分组作出相应对数函数的图象.观察图象,你能发现它们有哪些共同特征吗?
图 象 性 质
a > 1 0 < a < 1
定义域 : ( 0,+∞)
值 域 : R
过定点(1 ,0), 即当x =1时,y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
y
x
0
y
x
0
(1,0)
(1,0)
对数函数y=logax (a>0,且a≠1)的图象与性质
当x>1时,y>0 当x=1时,y=0 当0
2、总结性质
练一练
分别画出下列函数的图象。(示意图)
(1)
(2)
例1 求下列函数的定义域:
(1)
(2)
(三)
解 :
解 :
由
得
∴函数
的定义域是
由
得
∴函数
的定义域是
由具体函数式求定义域,考虑以下几个方面:
(1)分母不等于0;
(2)偶次方根被开方数非负;
(3)零指数幂底数不为0;
(4)对数式考虑真数大于0;
(5)实际问题要有实际意义.
【提升总结】
我练练我掌握
1. 求下列函数的定义域:
(3)
(4)
(1)
( 2 )
解:(1){x|x<1}
(2) {x|x>0且x≠1}
(3){x|x< }
(4) {x|x≥1}
当堂检测
3.求下列函数的定义域:
2、分别画出下列函数的图象。(示意图)
(1)
(2)
(2)
(1)
1、判断下列函数是否为对数函数。
(1)y =2 loga x (a>0,且a≠ 1 )
(2)y = loga x2 (a>0,且a≠ 1 )
通过本节的学习,说出你的收获。
数形结合
对数函数
图 象
性 质
概 念
课堂小结
(1) 类比记忆指数函数和对数函数。
(2)看见函数式想图像,结合图像记性质。
课后作业
必做题
课本 练习2、
课本 习题2.2 A 组7、
选做题
课本 习题2.2 B 组2
课后能力提升:根据如图所示的四个对数函 数图象,比较a, b, c, d的大小。
x
y
1
祝同学们学习进步!
