人教A版高中数学必修1第二章2.2.2对数函数及其性质课件(16张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第二章2.2.2对数函数及其性质课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 184.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 17:17:40 | ||
图片预览






文档简介
对数函数及其性质
由前面的学习我们知道:如果有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· ,1个这样的细胞分裂x次会得到多少个细胞?
如果知道了细胞的个数y,如何确定分裂的次数x呢?
由对数式与指数式的互化可知:
上式可以看作以y为自变量的函数表达式
对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即
这就是本节课要学习的:
定义:函数
,且
叫做对数函数,其中x是自变量,函数的定义域是(0,+∞)。
对数函数及其性质
,
对数函数
判断:以下函数是对数函数的是 ( )
A. y=(logax)+1(a>0且a≠1)
B. y=loga(2x)(a>0且a≠1)
C.y=lnx
D. y=2logax(a>0且a≠1)
小试牛刀
C
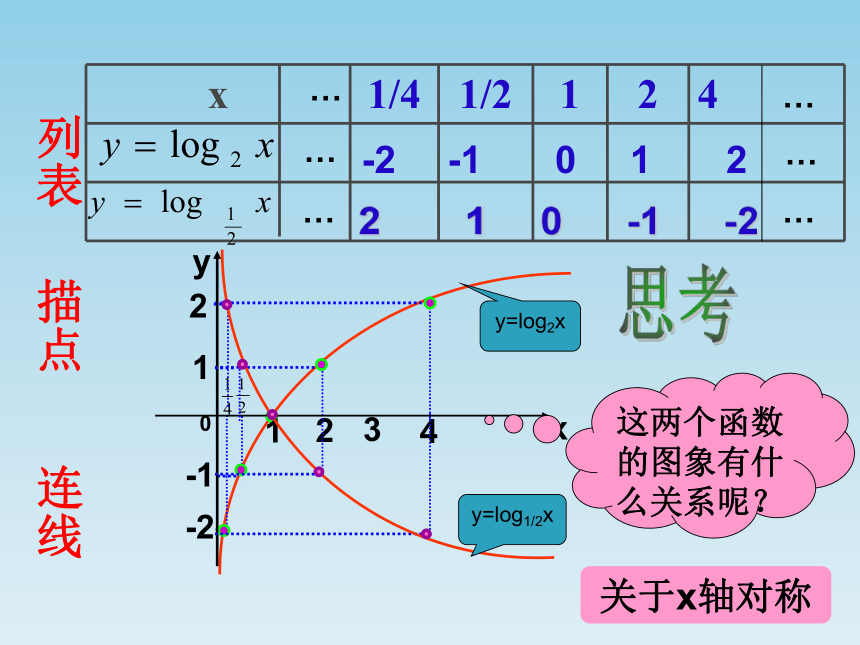
二.对数函数的图象:
1.描点画图
的变量x,y的对应值对调即可得到
y=logax(a>0,a≠1)的变量对应值表如下.
注意只要把指数函数y=ax (a>0,a≠1)
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
y=log1/2x
y=log2x
对数函数及其性质
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
研究内容:定义域、值域、特殊点、单调性.
类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
3.对数函数的图象与性质:
函数
y = log a x ( a>0 且 a≠1 )
底数
a > 1
0 < a < 1
图象
定义域
值域
定点
单调性
1
x
y
o
1
x
y
o
( 0 , + ∞ )
R
( 1 , 0 ) 即 x = 1 时,y = 0
在 ( 0 , + ∞ ) 上是增函数
在 ( 0 , + ∞ ) 上是减函数
例1:求下列函数的定义域:
(1) y=logax2 (2) y=loga(4-x)
解:
(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为
?-???? ? (0,+??
(2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为
(-??4)
习题讲解
例1中求定义域时应注意:
对数的真数大于0,底数大于0且不等于1;
使式子符合实际背景;
练一练
例2:函数f(x)=loga(x-1)的图像恒过定点 _____.
解:由于对数函数y=logax恒过定点(1,0),即当x=1时,y=0.那么要求f(x)恒过定点,只需令x-1=1即可,即x=2时,y=0.所以f(x)恒过定点(2,0)
因此,对数函数求过定点问题,只需令真数部分等于1即可.
例2:若函数f(x)是对数函数,且f(9)=2,当x 时,求f(x)的最大值与最小值.
解:由于f(x)为对数函数,则设f(x)=logax,由于f(9)=2,即loga9=2,即a2 =9,又a>0,故a=3.所以f(x)=log3x,则f(x)在所给区间上是增函数,所以f(x)的最大值为1,最小值为0.
对数函数及其性质
小结
(1)本节要求掌握对数函数的概念、图象和性质.
(2)在理解对数函数的定义的基础上,掌握对数函数的图象和性质的应用是本小节的重点.
作业:P74 习题2.2 A组 第7题
由前面的学习我们知道:如果有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· ,1个这样的细胞分裂x次会得到多少个细胞?
如果知道了细胞的个数y,如何确定分裂的次数x呢?
由对数式与指数式的互化可知:
上式可以看作以y为自变量的函数表达式
对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即
这就是本节课要学习的:
定义:函数
,且
叫做对数函数,其中x是自变量,函数的定义域是(0,+∞)。
对数函数及其性质
,
对数函数
判断:以下函数是对数函数的是 ( )
A. y=(logax)+1(a>0且a≠1)
B. y=loga(2x)(a>0且a≠1)
C.y=lnx
D. y=2logax(a>0且a≠1)
小试牛刀
C
二.对数函数的图象:
1.描点画图
的变量x,y的对应值对调即可得到
y=logax(a>0,a≠1)的变量对应值表如下.
注意只要把指数函数y=ax (a>0,a≠1)
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
y=log1/2x
y=log2x
对数函数及其性质
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
研究内容:定义域、值域、特殊点、单调性.
类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
3.对数函数的图象与性质:
函数
y = log a x ( a>0 且 a≠1 )
底数
a > 1
0 < a < 1
图象
定义域
值域
定点
单调性
1
x
y
o
1
x
y
o
( 0 , + ∞ )
R
( 1 , 0 ) 即 x = 1 时,y = 0
在 ( 0 , + ∞ ) 上是增函数
在 ( 0 , + ∞ ) 上是减函数
例1:求下列函数的定义域:
(1) y=logax2 (2) y=loga(4-x)
解:
(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为
?-???? ? (0,+??
(2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为
(-??4)
习题讲解
例1中求定义域时应注意:
对数的真数大于0,底数大于0且不等于1;
使式子符合实际背景;
练一练
例2:函数f(x)=loga(x-1)的图像恒过定点 _____.
解:由于对数函数y=logax恒过定点(1,0),即当x=1时,y=0.那么要求f(x)恒过定点,只需令x-1=1即可,即x=2时,y=0.所以f(x)恒过定点(2,0)
因此,对数函数求过定点问题,只需令真数部分等于1即可.
例2:若函数f(x)是对数函数,且f(9)=2,当x 时,求f(x)的最大值与最小值.
解:由于f(x)为对数函数,则设f(x)=logax,由于f(9)=2,即loga9=2,即a2 =9,又a>0,故a=3.所以f(x)=log3x,则f(x)在所给区间上是增函数,所以f(x)的最大值为1,最小值为0.
对数函数及其性质
小结
(1)本节要求掌握对数函数的概念、图象和性质.
(2)在理解对数函数的定义的基础上,掌握对数函数的图象和性质的应用是本小节的重点.
作业:P74 习题2.2 A组 第7题
