人教A版高中数学必修1第三章3.1.1方程的根与函数的零点课件(17张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.1.1方程的根与函数的零点课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 558.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 17:00:18 | ||
图片预览




文档简介
y
-2 0 2 4 6 x
8
6
4
2
-2
-4
普通高中课程标准实验教科书
人教A版数学必修1第三章 函数的应用 3.1.1节
函数的零点
1.理解函数零点的概念;
2.会求简单函数的零点 ;
3.理解函数图像与x轴的交点的横坐标和相应方程的实数根的关系;
4.理解零点存在性定理。
学习 目 标
引例:
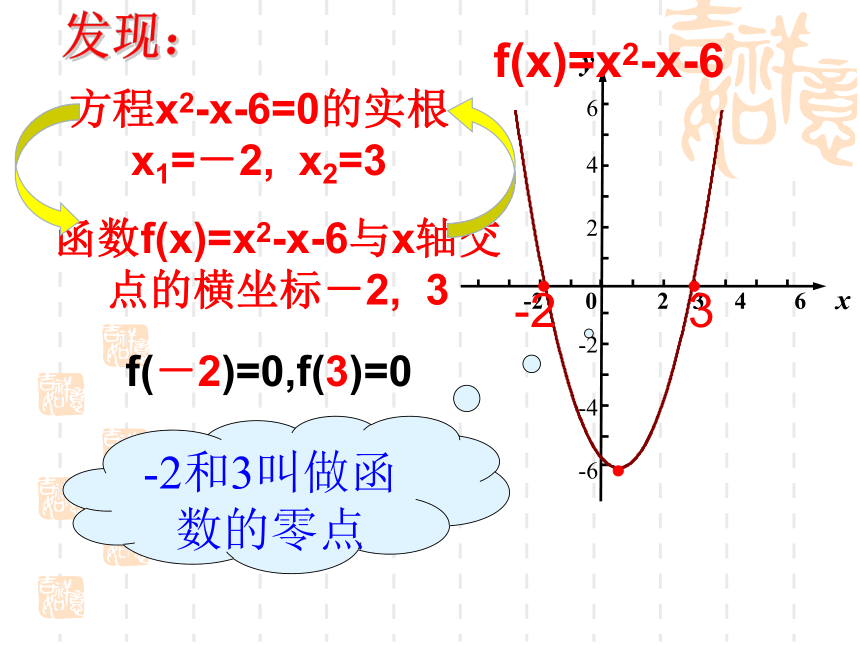
已知函数y=x2-x-6,
⑴当x为何值时,y=0?⑵作出函数的简图.
⑴解:令y=0, x2-x-6=0
(x-3)(x+2)=0
x1=-2,x2=3
∴当x = -2或3时,y=0
令y=0即x2-x-6=0的实根 是x1=-2,x2=3
y
-2 0 2 3 4 6 x
6
4
2
-2
-4
-6
f(-2)=0,f(3)=0
y
-2 0 2 3 4 6 x
6
4
2
-2
-4
-6
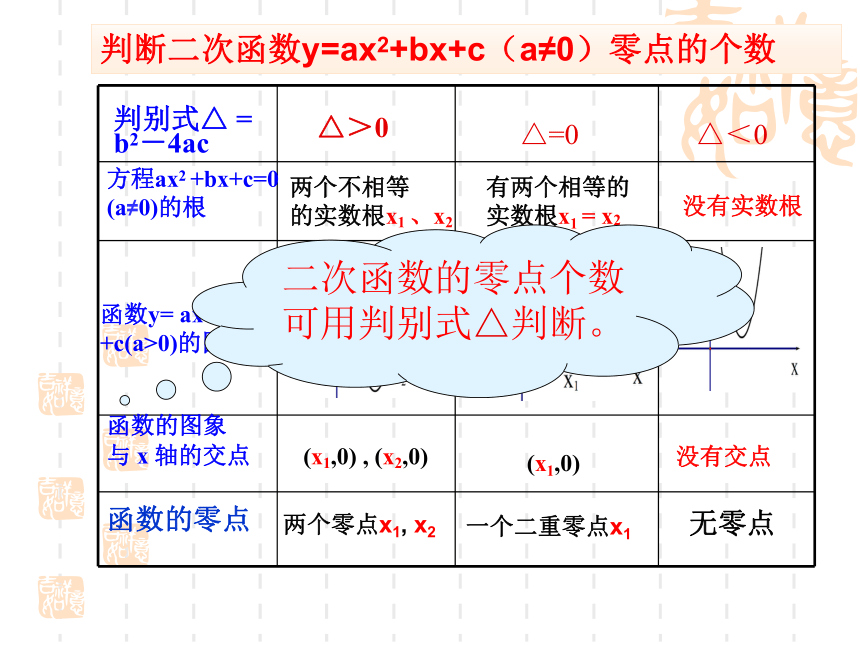
发现:
-2
3
方程x2-x-6=0的实根 x1=-2, x2=3
f(x)=x2-x-6
函数f(x)=x2-x-6与x轴交点的横坐标-2, 3
-2和3叫做函数的零点
解:(1)对应方程x2-2x-3 =0
△=4+12=16>0
方程有两根,故函数有两个零点。
(2)对应方程x2-2x+1 =0
△=4-4=0
方程有一根 ,故函数有一个零点。
(3)对应方程x2-2x+3 =0
△=-8﹤0
方程无实根,故函数没有零点。
练习:判断下列一元二次函数有几个零点。
转化
函数的零点
方程ax2 +bx+c=0
(a≠0)的根
函数y= ax2 +bx
+c(a>0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
两个零点x1, x2
一个二重零点x1
无零点
判断二次函数y=ax2+bx+c(a≠0)零点的个数
二次函数的零点个数可用判别式△判断。
函数零点的定义:
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
生成概念:
方程f(x) =0
的实数根
函数y=f(x)的零点
函数零点方程根,
形数本是同根生。
形
数
函数y=f(x)的图象与x轴交点的横坐标
等价关系
o
x
y
(1,0)
(-2,0)
0, 4
-2, 1
(2)图像法。
小试牛刀:
零点不是一个点,而是一个实数。
总结:求函数零点的方法
(1)代数法;
判断下列方程有无实根,若有实根,有几个?
问题情景:
如何求不能用公式求解的方程的根呢?
转化
(1)
(2)
问题1:看电影时,我们会错过一些镜头,但我们仍能推测出被忽略的片段。现我们有以下两组镜头,哪一组镜头说明小孩的行程一定曾渡过河?
生活情景:
问题2:将河流抽象成x轴,将前后两个位置视为A、B两点。请问当A、B与x轴有怎样的位置关系时,A、B间的一段连续不断的函数图象与x轴一定会有交点?
问题3:满足条件的函数图象与x轴的交点一定在(a,b)内吗?即函数的零点一定在(a,b)内吗?
问题4:如图,函数y=f(x)在[a,b]的图象,A、B是函数图象的端点,A、B在x轴的上下两侧的位置关系,如何用数学式子来表示?
表示点A、B在x轴的两侧。
零点存在性定理:
如果函数y=f(x)在区间 上的图象是 的一条曲线,并且有 ,那么,函数y=f(x)在区间 ,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的一个根.
生成概念:
连续不断
f(a)·f(b)<0
(a,b)内有零点
[a,b]
例1:判断下列方程有无实根,若有实根,有几个?
典例分析:
A(-1,0) B.(0,1) C.(1,2) D.(2,3)
A(-1,0) B.(0,1) C.(1,2) D.(2,3)
典例分析:
B
B
2. 方法:
3. 思想:
1. 知识:
函数零点的概念、零点存在定理
求函数零点的方法
数形结合、函数与方程
从特殊到一般的数学思想.
课堂小结
-2 0 2 4 6 x
8
6
4
2
-2
-4
普通高中课程标准实验教科书
人教A版数学必修1第三章 函数的应用 3.1.1节
函数的零点
1.理解函数零点的概念;
2.会求简单函数的零点 ;
3.理解函数图像与x轴的交点的横坐标和相应方程的实数根的关系;
4.理解零点存在性定理。
学习 目 标
引例:
已知函数y=x2-x-6,
⑴当x为何值时,y=0?⑵作出函数的简图.
⑴解:令y=0, x2-x-6=0
(x-3)(x+2)=0
x1=-2,x2=3
∴当x = -2或3时,y=0
令y=0即x2-x-6=0的实根 是x1=-2,x2=3
y
-2 0 2 3 4 6 x
6
4
2
-2
-4
-6
f(-2)=0,f(3)=0
y
-2 0 2 3 4 6 x
6
4
2
-2
-4
-6
发现:
-2
3
方程x2-x-6=0的实根 x1=-2, x2=3
f(x)=x2-x-6
函数f(x)=x2-x-6与x轴交点的横坐标-2, 3
-2和3叫做函数的零点
解:(1)对应方程x2-2x-3 =0
△=4+12=16>0
方程有两根,故函数有两个零点。
(2)对应方程x2-2x+1 =0
△=4-4=0
方程有一根 ,故函数有一个零点。
(3)对应方程x2-2x+3 =0
△=-8﹤0
方程无实根,故函数没有零点。
练习:判断下列一元二次函数有几个零点。
转化
函数的零点
方程ax2 +bx+c=0
(a≠0)的根
函数y= ax2 +bx
+c(a>0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
两个零点x1, x2
一个二重零点x1
无零点
判断二次函数y=ax2+bx+c(a≠0)零点的个数
二次函数的零点个数可用判别式△判断。
函数零点的定义:
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
生成概念:
方程f(x) =0
的实数根
函数y=f(x)的零点
函数零点方程根,
形数本是同根生。
形
数
函数y=f(x)的图象与x轴交点的横坐标
等价关系
o
x
y
(1,0)
(-2,0)
0, 4
-2, 1
(2)图像法。
小试牛刀:
零点不是一个点,而是一个实数。
总结:求函数零点的方法
(1)代数法;
判断下列方程有无实根,若有实根,有几个?
问题情景:
如何求不能用公式求解的方程的根呢?
转化
(1)
(2)
问题1:看电影时,我们会错过一些镜头,但我们仍能推测出被忽略的片段。现我们有以下两组镜头,哪一组镜头说明小孩的行程一定曾渡过河?
生活情景:
问题2:将河流抽象成x轴,将前后两个位置视为A、B两点。请问当A、B与x轴有怎样的位置关系时,A、B间的一段连续不断的函数图象与x轴一定会有交点?
问题3:满足条件的函数图象与x轴的交点一定在(a,b)内吗?即函数的零点一定在(a,b)内吗?
问题4:如图,函数y=f(x)在[a,b]的图象,A、B是函数图象的端点,A、B在x轴的上下两侧的位置关系,如何用数学式子来表示?
表示点A、B在x轴的两侧。
零点存在性定理:
如果函数y=f(x)在区间 上的图象是 的一条曲线,并且有 ,那么,函数y=f(x)在区间 ,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的一个根.
生成概念:
连续不断
f(a)·f(b)<0
(a,b)内有零点
[a,b]
例1:判断下列方程有无实根,若有实根,有几个?
典例分析:
A(-1,0) B.(0,1) C.(1,2) D.(2,3)
A(-1,0) B.(0,1) C.(1,2) D.(2,3)
典例分析:
B
B
2. 方法:
3. 思想:
1. 知识:
函数零点的概念、零点存在定理
求函数零点的方法
数形结合、函数与方程
从特殊到一般的数学思想.
课堂小结
