人教A版高中数学必修1第三章3.1.2用二分法求方程的近似解课件(19张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.1.2用二分法求方程的近似解课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 232.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 17:19:22 | ||
图片预览


文档简介
课题:用二分法求方程的近似解
难点名称:根据精确度得出近似解
高一年级-必修一第三章3.1.2 节
目录
CONTENTS
2
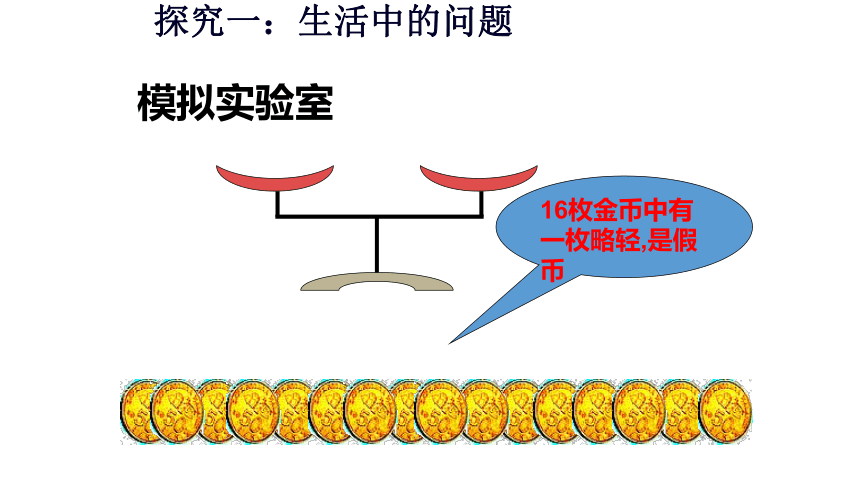
模拟实验室
16枚金币中有一枚略轻,是假币
探究一:生活中的问题
模拟实验室
模拟实验室
我在这里
模拟实验室
模拟实验室
模拟实验室
我在这里
模拟实验室
模拟实验室
哦,找到了啊!
通过这个小实验,你能想到什么样的方法缩小零点所在的范围呢?
例题分析:怎样计算函数 在区间(2,3)内精确到0.01零点近似值?
区间(a,b)
中点值m
f(m)的近似值
精确度|a-b|
(2,3)
2.5
-0.084
1
(2.5,3)
2.75
0.512
0.5
(2.5,2.75)
2.625
0.215
0.25
(2.5,2.625)
2.562 5
0.066
0.125
(2.5,2.562 5)
2.531 25
-0.009
0.0625
(2.531 25,2.562 5)
2.546 875
0.029
0.03125
(2.531 25,2.546 875)
2.539 062 5
0.01
0.015625
(2.531 25,2.539 062 5)
2.535 156 25
0.001
0.007813
探究三:给定精确度ε ,用二分法求函数f(x)零点近似值的步骤
1.确定区间[a,b],验证f(a).f(b)<0,给定精确度ε;
2.求区间(a,b)的中点x1,
3.计算f(x1)
(1)若f(x1)=0,则x1就是函数的零点;
(2)若f(a).f(x1)<0,则令b= x1(此时零点x0∈(a, x1) );
(3)若f(x1).f(b)<0,则令a= x1(此时零点x0∈( x1,,b));
4.判断是否达到精确度ε ,即若|a-b|< ε 则得到零点近似值a(或b),否则重复2~4
确定初始区间
求中点,算其函数值
缩小区间
算长度,比精确度
下结论
返
回
用二分法求方程的近似解一般步骤:
1.下列函数中,不能用二分法求零点的是( )
小试牛刀
B
2.用二分法求f(x)=0的近似解,
f(1)=-2,f(1.5)=0.625,
f(1.25)=-0.984,
f(1.375)=-0.260,
下一个求f(m),则m=________.
1.4375
B
3.已知 在区间
(1,2)内有一个零点x,若用二分
法求x的近似值(精确度0.1),则
需要将区间等分的次数为( )
A.3 B.4 C.5 D.6
如果在一个风雨交加的夜里查找线路,从某水库闸房到防洪指挥部的电话线路发生了故障.这是一条10 km长的线路,如何迅速查出故障所在?
如果沿着线路一小段一小段查找,困难很多.每查一个点要爬一次电线杆子,10 km长,大约有200多根电线杆子.
想一想,维修线路的工人师傅怎样工作最合理?每查一次,可以把待查的线路长度缩减一半,算一算,要把故障可能发生的范围缩小到50 m~100 m左右,即一两根电线杆附近,要查多少次?
【分析】根据二分法原理求解.
学以致用
【解析】(1)如图,他首先从中点C查.用随身带的话机向两端测试时,发现AC段正常,断定故障在BC段,再到BC段中点D查,这次发现BD段正常,可见故障在CD段,再到CD中点E来查,依次查下去
(2)每查一次,可以把待查的线路长度缩减一半,因此,只要7次就够了.
【评析】此方案应该说方便、迅速、准确,而且很科学,在实际生活中处处有数学,碰到问题时多用数学方法去思考,会使我们变得更聪明,更具有数学素养.
函数
方程
转化思想
逼近思想
数学
源于生活
数学
用于生活
小结
二分法
数形结合
1.寻找解所在的区间
2.不断二分解所在的区间
3.根据精确度得出近似解
用二分法求
方程的近似解
算法思想
难点名称:根据精确度得出近似解
高一年级-必修一第三章3.1.2 节
目录
CONTENTS
2
模拟实验室
16枚金币中有一枚略轻,是假币
探究一:生活中的问题
模拟实验室
模拟实验室
我在这里
模拟实验室
模拟实验室
模拟实验室
我在这里
模拟实验室
模拟实验室
哦,找到了啊!
通过这个小实验,你能想到什么样的方法缩小零点所在的范围呢?
例题分析:怎样计算函数 在区间(2,3)内精确到0.01零点近似值?
区间(a,b)
中点值m
f(m)的近似值
精确度|a-b|
(2,3)
2.5
-0.084
1
(2.5,3)
2.75
0.512
0.5
(2.5,2.75)
2.625
0.215
0.25
(2.5,2.625)
2.562 5
0.066
0.125
(2.5,2.562 5)
2.531 25
-0.009
0.0625
(2.531 25,2.562 5)
2.546 875
0.029
0.03125
(2.531 25,2.546 875)
2.539 062 5
0.01
0.015625
(2.531 25,2.539 062 5)
2.535 156 25
0.001
0.007813
探究三:给定精确度ε ,用二分法求函数f(x)零点近似值的步骤
1.确定区间[a,b],验证f(a).f(b)<0,给定精确度ε;
2.求区间(a,b)的中点x1,
3.计算f(x1)
(1)若f(x1)=0,则x1就是函数的零点;
(2)若f(a).f(x1)<0,则令b= x1(此时零点x0∈(a, x1) );
(3)若f(x1).f(b)<0,则令a= x1(此时零点x0∈( x1,,b));
4.判断是否达到精确度ε ,即若|a-b|< ε 则得到零点近似值a(或b),否则重复2~4
确定初始区间
求中点,算其函数值
缩小区间
算长度,比精确度
下结论
返
回
用二分法求方程的近似解一般步骤:
1.下列函数中,不能用二分法求零点的是( )
小试牛刀
B
2.用二分法求f(x)=0的近似解,
f(1)=-2,f(1.5)=0.625,
f(1.25)=-0.984,
f(1.375)=-0.260,
下一个求f(m),则m=________.
1.4375
B
3.已知 在区间
(1,2)内有一个零点x,若用二分
法求x的近似值(精确度0.1),则
需要将区间等分的次数为( )
A.3 B.4 C.5 D.6
如果在一个风雨交加的夜里查找线路,从某水库闸房到防洪指挥部的电话线路发生了故障.这是一条10 km长的线路,如何迅速查出故障所在?
如果沿着线路一小段一小段查找,困难很多.每查一个点要爬一次电线杆子,10 km长,大约有200多根电线杆子.
想一想,维修线路的工人师傅怎样工作最合理?每查一次,可以把待查的线路长度缩减一半,算一算,要把故障可能发生的范围缩小到50 m~100 m左右,即一两根电线杆附近,要查多少次?
【分析】根据二分法原理求解.
学以致用
【解析】(1)如图,他首先从中点C查.用随身带的话机向两端测试时,发现AC段正常,断定故障在BC段,再到BC段中点D查,这次发现BD段正常,可见故障在CD段,再到CD中点E来查,依次查下去
(2)每查一次,可以把待查的线路长度缩减一半,因此,只要7次就够了.
【评析】此方案应该说方便、迅速、准确,而且很科学,在实际生活中处处有数学,碰到问题时多用数学方法去思考,会使我们变得更聪明,更具有数学素养.
函数
方程
转化思想
逼近思想
数学
源于生活
数学
用于生活
小结
二分法
数形结合
1.寻找解所在的区间
2.不断二分解所在的区间
3.根据精确度得出近似解
用二分法求
方程的近似解
算法思想
