人教A版高中数学必修1第三章3.2.1几类不同增长的函数模型课件(22张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.2.1几类不同增长的函数模型课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 529.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览






文档简介
1859年,当澳大利亚的一个农夫为了打猎而从外国弄来几只兔子后,一场可怕的生态灾难爆发了。兔子是出了名的快速繁殖者,在澳大利亚它没有天敌,数量不断翻番。1950年,澳大利亚的兔子的数量从最初的五只增加到了五亿只,这个国家绝大部分地区的庄稼或草地都
遭到了极大损失。绝望之中,
人们从巴西引入了多发黏液瘤
病,以对付迅速繁殖的兔子。
整个20世纪中期,澳大利亚的
灭兔行动从未停止过。
创设情境
几类不同增长的函数模型
问题1. 假设你有一笔资金用于投资,现有三种投资方案供你选 择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
问题探究
回报值
日回报
累积回报
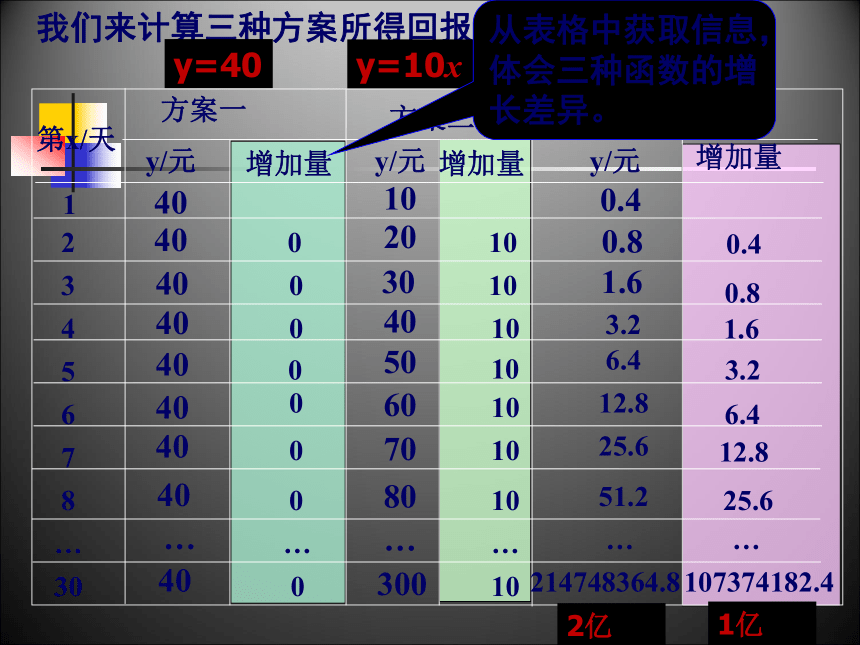
我们来计算三种方案所得回报的增长情况:
第x/天
方案一
方案二
方案三
y/元
y/元
y/元
增加量
增加量
增加量
1
2
3
40
40
40
0
0
10
20
30
10
10
0.4
0.8
1.6
0.4
0.8
0
4
5
6
7
8
…
30
…
…
…
…
…
…
40
40
40
40
40
40
0
0
0
0
0
40
50
60
70
80
300
10
10
10
10
10
10
3.2
6.4
12.8
25.6
51.2
214748364.8
1.6
3.2
6.4
12.8
25.6
107374182.4
y=40
y=10x
y=0.4×2x-1
从表格中获取信息,体会三种函数的增长差异。
2亿
1亿
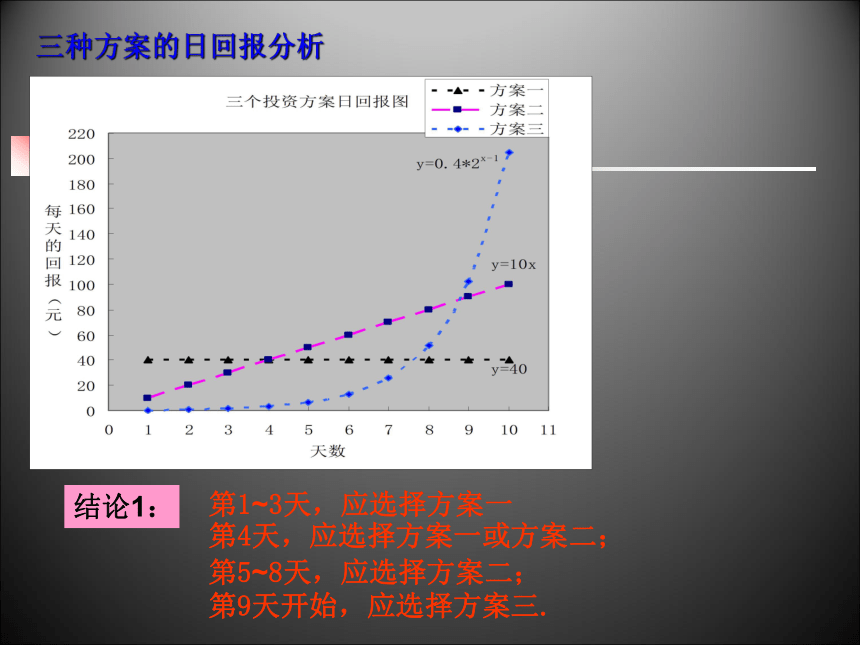
三种方案的日回报分析
第1~3天,应选择方案一
第4天,应选择方案一或方案二;
第9天开始,应选择方案三.
第5~8天,应选择方案二;
结论1:
结论二:投资1 ~ 6天,应选择方案一;
投资7天,可选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天以上(含11天),应选择方案三。
总天数
回报
方案
一
二
三
40
1 2 3 4 5 6 7 8 9 10 11
80 120 160 200 240 280 320 360 400 440
10 30 60 100 150 210 280 360 450 550 660
0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4409.2818.8
下面再看累计的回报数:
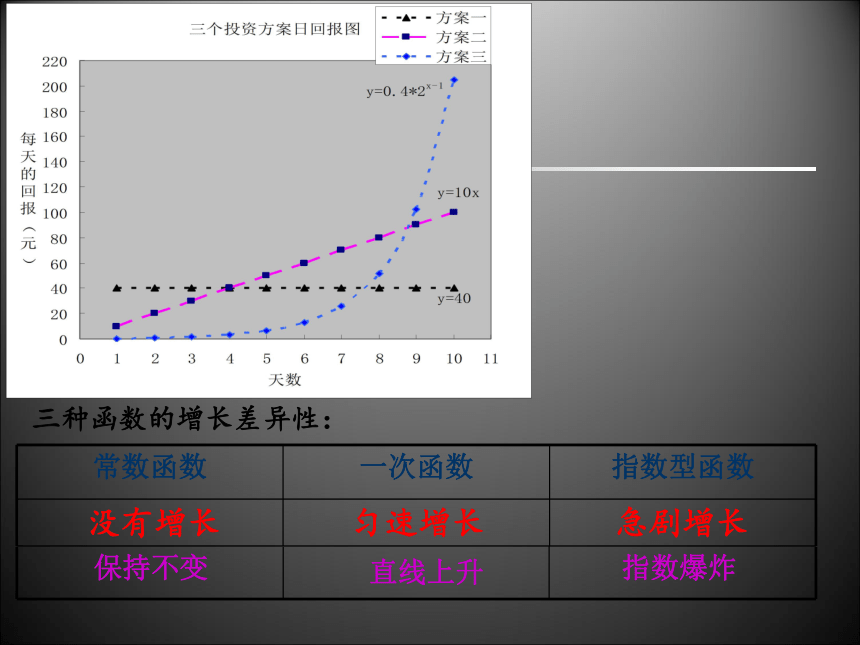
常数函数
一次函数
指数型函数
三种函数的增长差异性:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
学好函数可以帮大家做出最佳的方案选择,这样你就可以更快更好的积累财富。
问题2. 经过科学的选择和不懈的努力,你的投资终于给你带来了爆炸式的回报,现在你有了自己的公司,为了实现1000万元利润的目标,你的助手为你制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元。 现有三个奖励模型:
问:其中哪个模型能符合你公司的要求?
问题探究
若奖金不超过销售利润的25%,则上述模型还适用吗?
我们不妨先作出函数图象:
400
600
800
1000
1200
200
x
o
y=5
y=0.25x
通过观察函数图象得到初步结论:按对数模型进行奖励时符合公司的要求。
下面通过计算确认以上判断
对数增长模型比较适合于描述增长速度平缓的变化规律
400
600
800
1000
1200
200
x
o
y=5
y=0.25x
首先计算哪个模型的奖金不超过5万
对于模型 y=0.25x,它在 [10,1000]上是 递增
当 x=20 时,y=5,所以 x > 20 时,y>5,因此该模型 不符合要求;
单调性
x=?
哪个范围?
符合要求否?
所以,当 有
用计算机作图得它在[10,1000]上为减函数,所以有
即奖金不会超过利润的25%,
所以模型 能符合公司要求。
再计算按该模型奖金 y 是否不超过利润 x 的25%
当 是否有
当 是否有
用计算机作图得它在[10,1000]上为减函数,
再计算按该模型奖金 y 是否不超过利润 x 的25%
O
x
y
思维拓展
(1)如果从员工的角度考虑,哪个模型更好呢?
如果从双方共赢的角度看呢?
(2)如果这个模型2实施后,你觉得公司后续发 展会如何?你有什么对策吗?
10万~ 50万,奖金不超过2万
50万~ 200万,奖金不超过4万
200万~ 1000万, 奖金不超过20万
在你的要求下,你的助手为你重新制定了奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,要求如下:
请选择适当的函数模型,用图象表达助手的设计方案.
思维拓展
O
x
y
O
x
y
O
x
y
x
O
y
O
200
50
10
1000
20
4
2
1.几种常见函数的增长情况:
2.研究函数的方法:
解析法, 列表法,图象法。
常数函数
一次函数
指数函数
对数函数
没有增长
直线上升
指数爆炸
平缓增长
知识总结
实际问题
函数问题
建立模型
抽象概括
解析法
图像法
列表法
形成思维
1.当x越来越大时,增长速度最快的是( )
D
2.一次实验中,x,y函数关系与下列哪类函数最接近( )
A
x
1
2
3
4
5
6
y
0.25
0.49
0.76
1
1.26
1.51
课堂练习
3.一次实验中,x,y函数关系与下列哪类函数最接近( )
x
1.99
3.0
4.0
5.1
6.12
y
1.5
4.04
7.5
12
18.01
C
4. 时有( )
A
课堂练习
探索:
幂函数
指数函数
对数函数 的增长差异性.
课程延伸
谢谢观看
遭到了极大损失。绝望之中,
人们从巴西引入了多发黏液瘤
病,以对付迅速繁殖的兔子。
整个20世纪中期,澳大利亚的
灭兔行动从未停止过。
创设情境
几类不同增长的函数模型
问题1. 假设你有一笔资金用于投资,现有三种投资方案供你选 择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
问题探究
回报值
日回报
累积回报
我们来计算三种方案所得回报的增长情况:
第x/天
方案一
方案二
方案三
y/元
y/元
y/元
增加量
增加量
增加量
1
2
3
40
40
40
0
0
10
20
30
10
10
0.4
0.8
1.6
0.4
0.8
0
4
5
6
7
8
…
30
…
…
…
…
…
…
40
40
40
40
40
40
0
0
0
0
0
40
50
60
70
80
300
10
10
10
10
10
10
3.2
6.4
12.8
25.6
51.2
214748364.8
1.6
3.2
6.4
12.8
25.6
107374182.4
y=40
y=10x
y=0.4×2x-1
从表格中获取信息,体会三种函数的增长差异。
2亿
1亿
三种方案的日回报分析
第1~3天,应选择方案一
第4天,应选择方案一或方案二;
第9天开始,应选择方案三.
第5~8天,应选择方案二;
结论1:
结论二:投资1 ~ 6天,应选择方案一;
投资7天,可选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天以上(含11天),应选择方案三。
总天数
回报
方案
一
二
三
40
1 2 3 4 5 6 7 8 9 10 11
80 120 160 200 240 280 320 360 400 440
10 30 60 100 150 210 280 360 450 550 660
0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4409.2818.8
下面再看累计的回报数:
常数函数
一次函数
指数型函数
三种函数的增长差异性:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
学好函数可以帮大家做出最佳的方案选择,这样你就可以更快更好的积累财富。
问题2. 经过科学的选择和不懈的努力,你的投资终于给你带来了爆炸式的回报,现在你有了自己的公司,为了实现1000万元利润的目标,你的助手为你制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元。 现有三个奖励模型:
问:其中哪个模型能符合你公司的要求?
问题探究
若奖金不超过销售利润的25%,则上述模型还适用吗?
我们不妨先作出函数图象:
400
600
800
1000
1200
200
x
o
y=5
y=0.25x
通过观察函数图象得到初步结论:按对数模型进行奖励时符合公司的要求。
下面通过计算确认以上判断
对数增长模型比较适合于描述增长速度平缓的变化规律
400
600
800
1000
1200
200
x
o
y=5
y=0.25x
首先计算哪个模型的奖金不超过5万
对于模型 y=0.25x,它在 [10,1000]上是 递增
当 x=20 时,y=5,所以 x > 20 时,y>5,因此该模型 不符合要求;
单调性
x=?
哪个范围?
符合要求否?
所以,当 有
用计算机作图得它在[10,1000]上为减函数,所以有
即奖金不会超过利润的25%,
所以模型 能符合公司要求。
再计算按该模型奖金 y 是否不超过利润 x 的25%
当 是否有
当 是否有
用计算机作图得它在[10,1000]上为减函数,
再计算按该模型奖金 y 是否不超过利润 x 的25%
O
x
y
思维拓展
(1)如果从员工的角度考虑,哪个模型更好呢?
如果从双方共赢的角度看呢?
(2)如果这个模型2实施后,你觉得公司后续发 展会如何?你有什么对策吗?
10万~ 50万,奖金不超过2万
50万~ 200万,奖金不超过4万
200万~ 1000万, 奖金不超过20万
在你的要求下,你的助手为你重新制定了奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,要求如下:
请选择适当的函数模型,用图象表达助手的设计方案.
思维拓展
O
x
y
O
x
y
O
x
y
x
O
y
O
200
50
10
1000
20
4
2
1.几种常见函数的增长情况:
2.研究函数的方法:
解析法, 列表法,图象法。
常数函数
一次函数
指数函数
对数函数
没有增长
直线上升
指数爆炸
平缓增长
知识总结
实际问题
函数问题
建立模型
抽象概括
解析法
图像法
列表法
形成思维
1.当x越来越大时,增长速度最快的是( )
D
2.一次实验中,x,y函数关系与下列哪类函数最接近( )
A
x
1
2
3
4
5
6
y
0.25
0.49
0.76
1
1.26
1.51
课堂练习
3.一次实验中,x,y函数关系与下列哪类函数最接近( )
x
1.99
3.0
4.0
5.1
6.12
y
1.5
4.04
7.5
12
18.01
C
4. 时有( )
A
课堂练习
探索:
幂函数
指数函数
对数函数 的增长差异性.
课程延伸
谢谢观看
