人教A版数学必修1第三章3.1.2 用二分法求方程的近似解 课件(共16张PPT)
文档属性
| 名称 | 人教A版数学必修1第三章3.1.2 用二分法求方程的近似解 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 339.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 08:05:18 | ||
图片预览



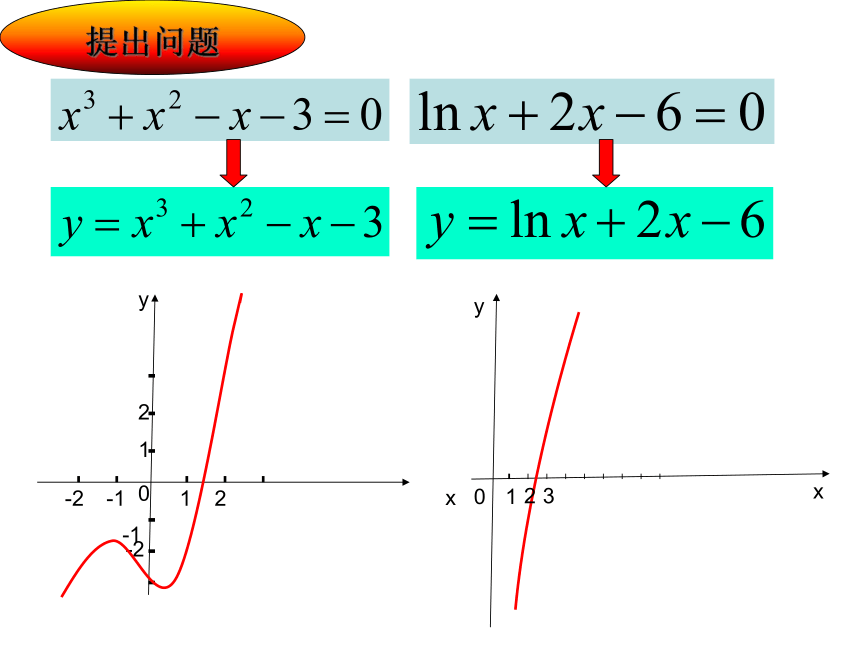


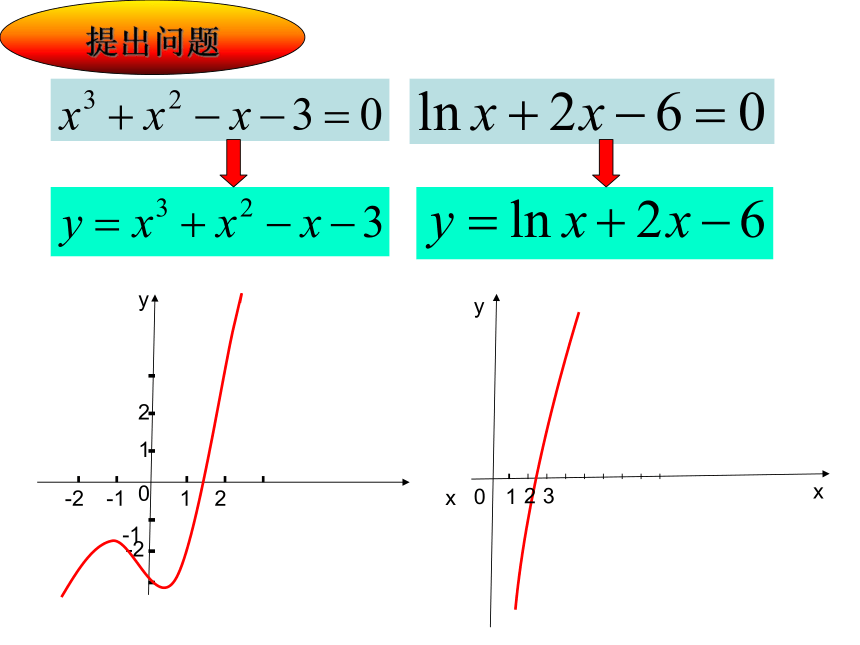
文档简介
§3.1.2 用二分法求方程的近似解
问题1:你能求下列方程的解吗?
提出问题
提出问题
问题2:能否有办法求解 ?
0
1
2
2
1
-1
-2
-1
-2
y
y
x
0
x
1
2
3
提出问题
实例导入
从城市A到附近郊区B的供电线路的某一处发生了故障,这是一条10km长的线路,每隔约100米有一根电线杆,如何迅速查出故障所在呢?
? 维修电工师傅怎样工作合理?
想一想
?
如图,设市区和郊区的所在处分别为点A、B(间距10km)
A
(市区)
这样每查一次,就可以把待查的线路长度缩减一半
C
B
(郊区)
D
E
取中点
实例导入
0
1
2
2
1
-1
-2
-1
-2
y
y
x
0
x
1
2
3
提出问题
探究1:检测函数零点的标准是什么?
探究2:利用求故障点的思路叙述出找寻函数零点的思路。
新知探究
二分法的定义:
概念形成
例:借助计算器用二分法求方程
的近似解(精确度0.1)
求方程 的近似解
求函数 零点的近似值
次数
区间长度:
1
2
3
4
0.5
所以方程的近似解为:
2.5
-0.084
2.5
3
0.25
0.125
0.0625
2.75
0.512
2.625
0.215
0.066
2.5625
2.5
2.75
2
3
由于|2.5625-2.5|=0.0625<0.1
2.5
2.75
2.625
2.5625
零点所在区间为[2,3]且
探究归纳
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
借助计算器或计算机用二分法求方程
的近似解(精确度0.1)
巩固新知
周而复始怎么办?
定区间,找中点,
零点落在异号间,
口 诀
反思小结 体会收获
中值计算两边看;
区间长度缩一半;
精确度上来判断.
本节课你学到了哪些知识?有哪些收获?
1.下列函数中能用二分法求零点的是( )
2.用二分法求函数
在
值的过程中得到
则函数的零点落在区间( ).
A (1,1.25) B (1.25,1.5) C (1.5,2) D 不能确定
3.从上海到美国旧金山的海底电缆有15个接点,现在某 接点发生故障,需及时修理,为了尽快断定故障发生点, 一般至少需要检查接点的个数为 ? 个.
内零点近似
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
课堂检测
巩固提高 课外练习
1、课堂作业:
课本P92 第3题,第5题
2、课外作业:
(1)阅读课本P91 《中外历史上的方程求解》;
(2)12只金表中有一只份量略轻,如何用一架天平秤,在秤量次数最少的情况下分辩出来?
问题1:你能求下列方程的解吗?
提出问题
提出问题
问题2:能否有办法求解 ?
0
1
2
2
1
-1
-2
-1
-2
y
y
x
0
x
1
2
3
提出问题
实例导入
从城市A到附近郊区B的供电线路的某一处发生了故障,这是一条10km长的线路,每隔约100米有一根电线杆,如何迅速查出故障所在呢?
? 维修电工师傅怎样工作合理?
想一想
?
如图,设市区和郊区的所在处分别为点A、B(间距10km)
A
(市区)
这样每查一次,就可以把待查的线路长度缩减一半
C
B
(郊区)
D
E
取中点
实例导入
0
1
2
2
1
-1
-2
-1
-2
y
y
x
0
x
1
2
3
提出问题
探究1:检测函数零点的标准是什么?
探究2:利用求故障点的思路叙述出找寻函数零点的思路。
新知探究
二分法的定义:
概念形成
例:借助计算器用二分法求方程
的近似解(精确度0.1)
求方程 的近似解
求函数 零点的近似值
次数
区间长度:
1
2
3
4
0.5
所以方程的近似解为:
2.5
-0.084
2.5
3
0.25
0.125
0.0625
2.75
0.512
2.625
0.215
0.066
2.5625
2.5
2.75
2
3
由于|2.5625-2.5|=0.0625<0.1
2.5
2.75
2.625
2.5625
零点所在区间为[2,3]且
探究归纳
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
借助计算器或计算机用二分法求方程
的近似解(精确度0.1)
巩固新知
周而复始怎么办?
定区间,找中点,
零点落在异号间,
口 诀
反思小结 体会收获
中值计算两边看;
区间长度缩一半;
精确度上来判断.
本节课你学到了哪些知识?有哪些收获?
1.下列函数中能用二分法求零点的是( )
2.用二分法求函数
在
值的过程中得到
则函数的零点落在区间( ).
A (1,1.25) B (1.25,1.5) C (1.5,2) D 不能确定
3.从上海到美国旧金山的海底电缆有15个接点,现在某 接点发生故障,需及时修理,为了尽快断定故障发生点, 一般至少需要检查接点的个数为 ? 个.
内零点近似
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
课堂检测
巩固提高 课外练习
1、课堂作业:
课本P92 第3题,第5题
2、课外作业:
(1)阅读课本P91 《中外历史上的方程求解》;
(2)12只金表中有一只份量略轻,如何用一架天平秤,在秤量次数最少的情况下分辩出来?
