北师大版九上数学1.1菱形的性质和判定课堂讲义及练习(word版含答案)
文档属性
| 名称 | 北师大版九上数学1.1菱形的性质和判定课堂讲义及练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 440.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 21:50:10 | ||
图片预览


文档简介
菱形练习
1.1菱形的性质和判定
【菱形的性质】
1.菱形的定义
有一组邻边相等的平行四边形叫做菱形.
符号语言:
??∵四边形ABCD是平行四边形,且AB=BC,
??∴四边形ABCD是菱形
.
温馨提示:
①菱形必须满足两个条件:一是平行四边形;二是一组邻边相等;
②菱形是特殊的平行四边形,即当一个平行四边形满足一组邻边相等时,该平行四边形是菱形,不能错误地认为有一组邻边相等的四边形就是菱形;
③菱形的定义既提供了菱形的基本性质,也提供了基本判定方法。
2.菱形的性质
(1)菱形具有平行四边形的所有性质
.
(2)菱形的四条边都相等
.
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
.
(4)菱形是轴对称图形,它有两条对称轴,对角线所在直线就是它的对称轴.菱形又是中心对称图形,对角线的交点为对称中心.
菱形中相等的线段:AB
=
CD
=
AD
=
BC.OA
=
OC
,
OB
=
OD.
菱形中相等的角:∠AOB
=
∠DOC
=
∠AOD
=
∠BOC
=
90°?.∠ADC=∠ABC.∠DAB=∠DCB
∠1
=
∠2
=
∠3
=
∠4,∠5
=
∠6
=
∠7
=
∠8.
菱形中的全等三角形:
全等的等腰三角形有:,
全等的直角三角形有:
点拨:有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
(转化思想).
温馨提示:
①菱形具有平行四边形的一切性质;
②“菱形的对角线互相垂直”这一性质可用来证明两条线段互相垂直,“菱形的每一条对角线平分一组对角”这一性质可用来证明角相等;
③菱形的两条对角线分菱形为四个全等的直角三角形。
1、下列四边形中不一定为菱形的是( )
A.
对角线相等的平行四边形
B.
对角线平分一组对角的平行四边形
C.
对角线互相垂直的平行四边形
D.
用两个全等的等边三角形拼成的四边形
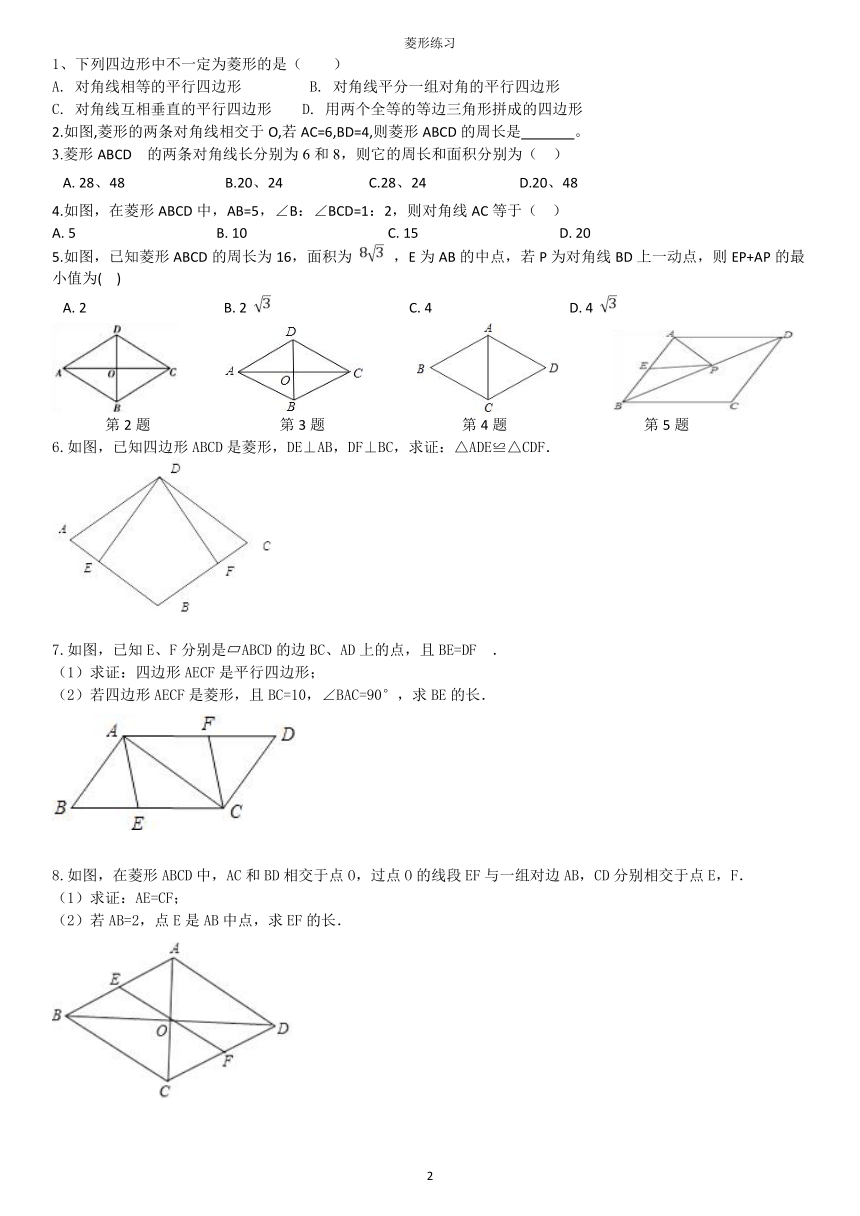
2.如图,菱形的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是
。
3.菱形ABCD
的两条对角线长分别为6和8,则它的周长和面积分别为(??
)
A.?28、48
???????????????????????????B.20、24?????????????????????????C.28、24???????????????????????????D.20、48?
4.如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于(??
)
A.?5?????????????????????????????????????????B.?10?????????????????????????????????????????C.?15?????????????????????????????????????????D.?20
5.如图,已知菱形ABCD的周长为16,面积为
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为(??
)
A.?2????????????????????????????????????????B.?2
????????????????????????????????????????C.?4????????????????????????????????????????D.?4
第2题
第3题
第4题
第5题
6.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF.
7.如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF
.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
8.如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
【菱形的判定】
1.
菱形的判定定理
(1)定义法:有一组邻边相等的平行四边形是菱形.
(2)对角线互相垂直的平行四边形是菱形
.
(3)四边相等的四边形是菱形
.
①证明一个四边形是菱形,一般情况下,先证明它是一个平行四边形,然后要么证明“一组邻边相等”,要么证明“对角线互相垂直”.若要直接证明一个四边形是菱形,只要证明“四条边相等”即可;
②对角线互相垂直平分的四边形是菱形;
③对角线平分一个内角的平行四边形是菱形。
1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
2.下列命题中正确的是(??
)
A.?对角线相等的四边形是菱形???
B.?对角线互相垂直的四边形是菱形
C.?对角线相等的平行四边形是菱形??D.?对角线互相垂直的平行四边形是菱形
3.四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是(
??)
A.?平行四边形???B.?矩形???C.?菱形??D.?正方形
4.如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形是一个特殊的四边形.
(1)这个特殊的四边形应该叫做________;
(2)请证明你的结论.
如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE.求证:四边形BCED是菱形.
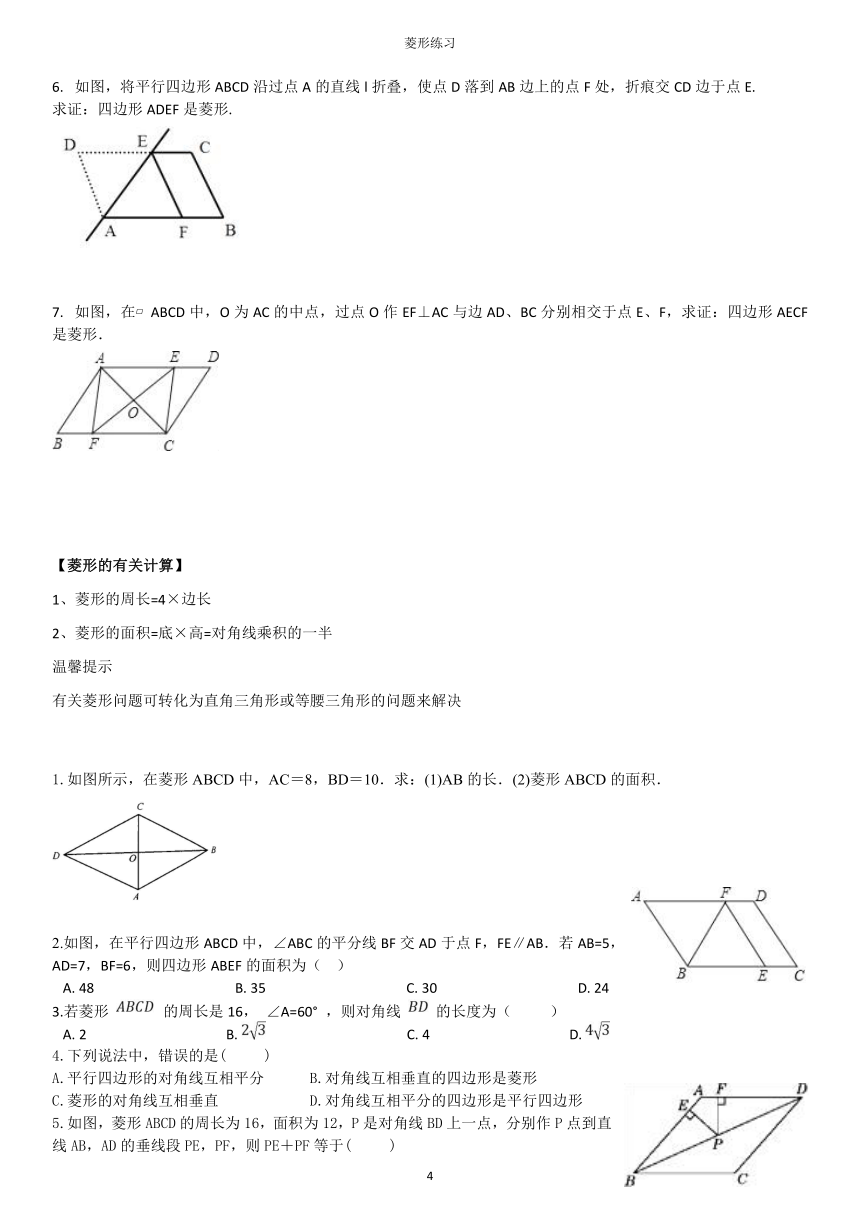
如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E.
求证:四边形ADEF是菱形.
如图,在?ABCD中,O为AC的中点,过点O作EF⊥AC与边AD、BC分别相交于点E、F,求证:四边形AECF是菱形.
【菱形的有关计算】
1、菱形的周长=4×边长
2、菱形的面积=底×高=对角线乘积的一半
温馨提示
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
1.如图所示,在菱形ABCD中,AC=8,BD=10.求:(1)AB的长.(2)菱形ABCD的面积.
2.如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,AD=7,BF=6,则四边形ABEF的面积为(??
)
A.?48?????????????????????????????????????????B.?35?????????????????????????????????????????C.?30?????????????????????????????????????????D.?24
3.若菱形
的周长是16,
∠A=60°
,则对角线
的长度为(
)
A.?2????????????????????????????????????????B.?????????????????????????????????????????C.?4????????????????????????????????????????D.?
4.下列说法中,错误的是(??
)
A.平行四边形的对角线互相平分
B.对角线互相垂直的四边形是菱形
C.菱形的对角线互相垂直
D.对角线互相平分的四边形是平行四边形
5.如图,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作P点到直线AB,AD的垂线段PE,PF,则PE+PF等于(??
)
A.?6??B.?3????C.?1.5??????D.?0.75
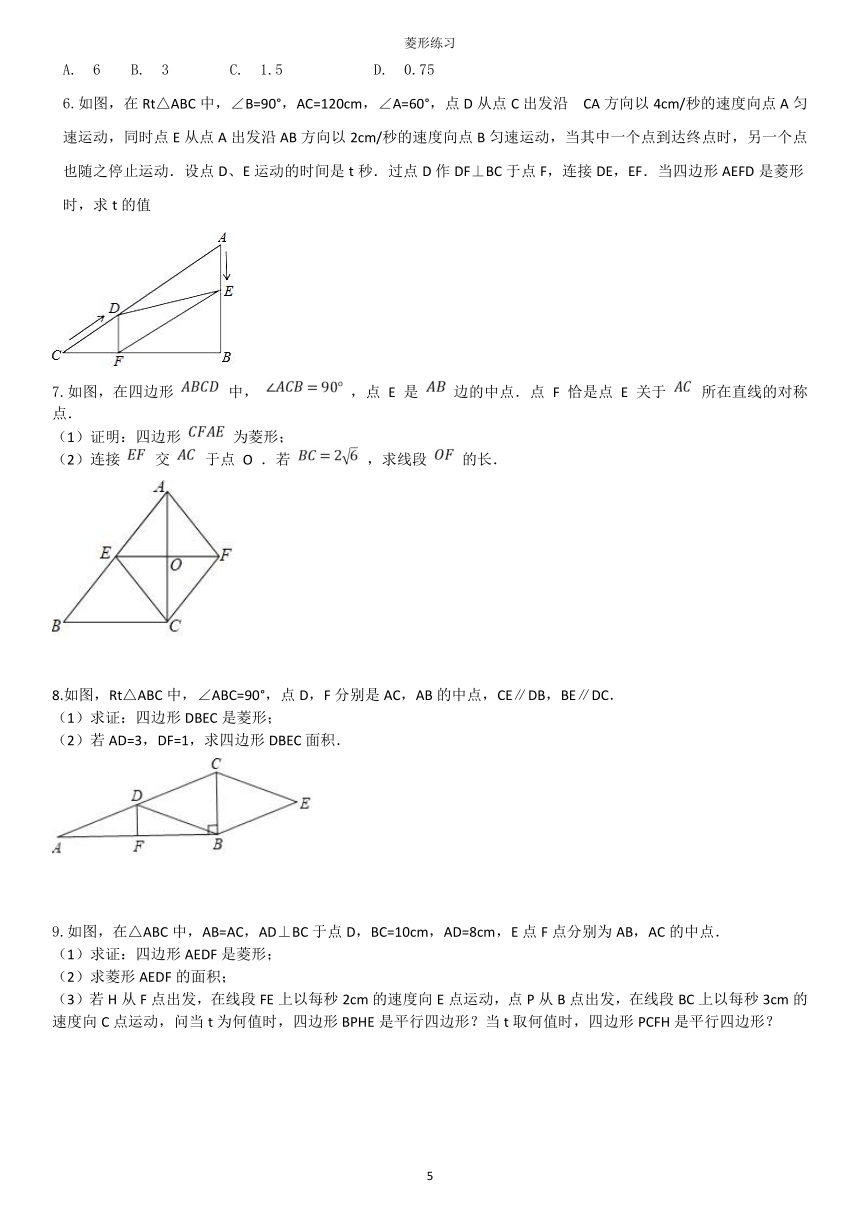
6.如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿
CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,求t的值
7.如图,在四边形
中,
,点
E
是
边的中点.点
F
恰是点
E
关于
所在直线的对称点.
(1)证明:四边形
为菱形;
(2)连接
交
于点
O
.若
,求线段
的长.
8.如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.
9.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
【课后练习】
1.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2
,则CE的长为________
第1题
第2题
第3题
第4题
2.如图,点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=________度.
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABC的周长是________.
4.如图,菱形ABC的对角线相交于点O,过点D作DE∥AC,且DE=
AC,连接CE、OE、AE,AE交OD于点F,若AB=2,∠ABC=60°,则AE的长________.
5.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形
中,
,
,则
的长为________.
6.如图:在△ABC中,∠BAC
=
,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
7.如图,在平行四边形
中,∠BAD的平分线交
于E,点
F
在
上,且
,连接
.
(1)判断四边形
的形状并证明;
(2)若
、
相交于点
O
,且四边形
的周长为
,
,求
的长度及四边形
的面积.
8.如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
9.如图:菱形的边长为,,对角线、相交于,求菱形的面积.
?
10.已知菱形的周长为,两个相邻对角之比为,求它的对角线长和面积.
11.如图,在中,,平分,于点,与交于点,.
求证:与互相垂直平分.
?
12.如图,在中,是的角平分线,,,交于点,请问是的角平分线吗?请说明理由.
答案
【菱形的性质】
1.A
2.
3.B
4.A
5.B
6.∵四边形ABCD是菱形,∴∠A=∠C,AD=CD,又∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°,
在△ADE和△CDF中,
,∴△ADE≌△CDF(AAS).
7.(1)证明:
∵
四边形ABCD是平行四边形,
,且
,
,
,
,四边形AECF是平行四边形.
(2)如图,∵四边形AECF是菱形,∴AE=EC,∴∠1=∠2,∵∠BAC=90°,
∴∠3=90°-∠2,∠4=90°-∠1,∴∠3=∠4∴AE=BE,∴
BE=AE=CE=BC=5
8.(1)证明:∵四边形ABCD是菱形,∴AO=CO,AB∥CD,∴∠EAO=∠FCO,∠AEO=∠CFO.
在△OAE和△OCF中,∠EAO=∠FCO,AO=CO,∠AEO=∠CFO,∴△AOE≌△COF,∴AE=CF;
解:∵E是AB中点,∴BE=AE=CF.∵BE∥CF,∴四边形BEFC是平行四边形,∵AB=2,∴EF=BC=AB=2.
【菱形的判定】
1.×
√
×
×
2.D
3.C
4.(1)菱形;(2)∵四边形是用两张等宽的纸条交叉重叠地放在一起而组成的图形,∴,,
∴四边形是平行四边形(对边相互平行的四边形是平行四边形);
过点分别作,边上的高为,.则(两纸条相同,纸条宽度相同);
∵平行四边形中,,即,∴.∴平行四边形为菱形
5.证明:∵
≌
,∴
?,在
和
中
,
∴
≌
?,∴
,又∵
,∴
?,∴
,
∴
,∴
,∴四边形BCED是菱形.
6.由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA∵四边形ABCD是平行四边形∴DE∥AF∴∠DEA=∠EAF
∴∠EAF=∠FEA∴AF=EF????∴AF=AD=DE=EF∴四边形ADEF是菱形.
7.
∵四边形ABCD是平行四边形,∴BC∥AD,∴AE∥CF,∴∠OAE=∠OCF,∵点O是AC的中点,∴OA=OC,
在△AOE和△COF中,
?∴△AOE≌△COF(ASA),∴AE=CF,∵AE∥CF,
∴四边形AECF是平行四边形,∵EF与AC垂直,∴四边形AECF是菱形
【菱形的有关计算】
1.(1)∵
四边形ABCD是菱形.∴
AC⊥BD,AO=AC,OB=BD.
又∵
AC=8,BD=10.
∴
AO=×8=4,OB=×10=5.在Rt△ABO中,∴
,∴
.
(2)由菱形的性质可知:
2.D
3.C
4.B
5.B
6.由题意CD=4t,AE=2t,
∵DF⊥BC于F,∴∠DFC=90°在Rt△DFC中,∵∠C=30°,
∴DF=
CD=2t,∴DF=AE,∵∠CFD=∠B=90°,∴DF∥CE,∴四边形DFEA是平行四边形,
∴当DF=AD时,四边形DFEA是菱形.∴120﹣4t=2t,∴t=20s,∴t=20s时,四边形DFEA是菱形.
7.(1)证明:
,点E是AB变的中点
点F恰是点E关于AC所在直线的对称点
四边形
为菱形
(2)解:∵四边形
是菱形,∴
,∴
,∴
8.(1)∵CE∥DB,BE∥DC,∴四边形DBEC为平行四边形.又∵Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴CD=BD=
AC,∴平行四边形DBEC是菱形
(2)解:∵点D,F分别是AC,AB的中点,AD=3,DF=1,∴DF是△ABC的中位线,AC=2AD=6,S△BCD=
S△ABC
∴BC=2DF=2.又∵∠ABC=90°,∴AB=
=
=4
.
∵平行四边形DBEC是菱形,∴S四边形DBEC=2S△BCD=S△ABC=
AB?BC=
×4
×2=4
9.(1)∵AB=AC,AD⊥BC,∴D为BC的中点.∵E、F分别为AB、AC的中点,∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,∴四边形AEDF是平行四边形.∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF,∴四边形AEDF是菱形
(2)解:∵EF为△ABC的中位线,∴EF=
BC=5.∵AD=8,AD⊥EF,∴S菱形AEDF=
AD?EF=
×8×5=20
(3)解:∵EF∥BC,∴EH∥BP.若四边形BPHE为平行四边形,则须EH=BP,∴5﹣2t=3t,解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形.∵EF∥BC,∴FH∥PC.
若四边形PCFH为平行四边形,则须FH=PC,∴2t=10﹣3t,解得:t=2,∴当t=2秒时,四边形PCFH为平行四边形
【课后练习】
1.
5
或
2.45
3.18
4.
5.
6.∵AD⊥BC,∴∠ADB=90°,∵∠BAC=90°,∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,∴∠B=∠CAD,
∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA),∴AE=EF(角平分线上的点到角两边的距离相等),
∵CE=CE,∴由勾股定理得:AC=CF,∵△ACG和△FCG中
?∴△ACG≌△FCG,∴∠CAD=∠CFG,∵∠B=∠CAD∴∠B=∠CFG,∴GF∥AB,∵AD⊥BC,EF⊥BC,∴AD∥EF,即AG∥EF,AE∥GF,
∴四边形AEFG是平行四边形,∵AE=EF,∴平行四边形AEFG是菱形.
7.(1)解:∵AE是∠BAF的角平分线,∴∠BAE=∠FAE,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠FAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE.∵AB=AF,∴BE=FA,∴四边形ABEF为平行四边形,∵AB=AF,∴四边形ABEF为菱形
(2)解:∵四边形ABEF为菱形,且周长为20,∴AB=5,AE⊥BF,BO=
FB=3,AE=2AO,
在Rt△AOB中,AO=
=4,∴AE=2AO=8,菱形ABEF面积=
AE×BF=
×8×6=24
8.(1)证明:∵在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,
∴AO=AC=3,BO=BD=4,∵AB=5,且32+42=52,∴AO2+BO2=AB2,
∴△AOB是直角三角形,且∠AOB=90°,
∴AC⊥BD,∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴BC=AB=5,∵S△ABC=AC?BO=BC?AH,
∴×6×4=×5×AH,解得:AH=.
9.:在菱形中,又在中,,∴,
,∴为等边三角形∴.
在菱形中,,∴为直角三角形,∴,
∴,∴,∴.
10.解:∵菱形的周长为,∴菱形的边长,∵两个相邻对角之比为,
∴,∴是等边三角形,∴,∵菱形对角线,∴,∴,∴菱形的面积.
11.:延长交于点.∵,,∴,即.
又∵,平分,∴.在与中,,∴,
∴.在与中,,∴,∴,
∴垂直平分(三合一).∴,在与中,,∴
∴,又∵.∴四边形为平行四边形,∵,∴四边形为菱形,∴与互相垂直平分.
12.解:是的角平分线,理由是:∵,,∴四边形是平行四边形,
∵,∴,∵是的角平分线,∴,
∴,∴,∴四边形是菱形,∴平分,即是的角平分线.
1.1菱形的性质和判定
【菱形的性质】
1.菱形的定义
有一组邻边相等的平行四边形叫做菱形.
符号语言:
??∵四边形ABCD是平行四边形,且AB=BC,
??∴四边形ABCD是菱形
.
温馨提示:
①菱形必须满足两个条件:一是平行四边形;二是一组邻边相等;
②菱形是特殊的平行四边形,即当一个平行四边形满足一组邻边相等时,该平行四边形是菱形,不能错误地认为有一组邻边相等的四边形就是菱形;
③菱形的定义既提供了菱形的基本性质,也提供了基本判定方法。
2.菱形的性质
(1)菱形具有平行四边形的所有性质
.
(2)菱形的四条边都相等
.
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
.
(4)菱形是轴对称图形,它有两条对称轴,对角线所在直线就是它的对称轴.菱形又是中心对称图形,对角线的交点为对称中心.
菱形中相等的线段:AB
=
CD
=
AD
=
BC.OA
=
OC
,
OB
=
OD.
菱形中相等的角:∠AOB
=
∠DOC
=
∠AOD
=
∠BOC
=
90°?.∠ADC=∠ABC.∠DAB=∠DCB
∠1
=
∠2
=
∠3
=
∠4,∠5
=
∠6
=
∠7
=
∠8.
菱形中的全等三角形:
全等的等腰三角形有:,
全等的直角三角形有:
点拨:有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
(转化思想).
温馨提示:
①菱形具有平行四边形的一切性质;
②“菱形的对角线互相垂直”这一性质可用来证明两条线段互相垂直,“菱形的每一条对角线平分一组对角”这一性质可用来证明角相等;
③菱形的两条对角线分菱形为四个全等的直角三角形。
1、下列四边形中不一定为菱形的是( )
A.
对角线相等的平行四边形
B.
对角线平分一组对角的平行四边形
C.
对角线互相垂直的平行四边形
D.
用两个全等的等边三角形拼成的四边形
2.如图,菱形的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是
。
3.菱形ABCD
的两条对角线长分别为6和8,则它的周长和面积分别为(??
)
A.?28、48
???????????????????????????B.20、24?????????????????????????C.28、24???????????????????????????D.20、48?
4.如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于(??
)
A.?5?????????????????????????????????????????B.?10?????????????????????????????????????????C.?15?????????????????????????????????????????D.?20
5.如图,已知菱形ABCD的周长为16,面积为
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为(??
)
A.?2????????????????????????????????????????B.?2
????????????????????????????????????????C.?4????????????????????????????????????????D.?4
第2题
第3题
第4题
第5题
6.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF.
7.如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF
.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
8.如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
【菱形的判定】
1.
菱形的判定定理
(1)定义法:有一组邻边相等的平行四边形是菱形.
(2)对角线互相垂直的平行四边形是菱形
.
(3)四边相等的四边形是菱形
.
①证明一个四边形是菱形,一般情况下,先证明它是一个平行四边形,然后要么证明“一组邻边相等”,要么证明“对角线互相垂直”.若要直接证明一个四边形是菱形,只要证明“四条边相等”即可;
②对角线互相垂直平分的四边形是菱形;
③对角线平分一个内角的平行四边形是菱形。
1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
2.下列命题中正确的是(??
)
A.?对角线相等的四边形是菱形???
B.?对角线互相垂直的四边形是菱形
C.?对角线相等的平行四边形是菱形??D.?对角线互相垂直的平行四边形是菱形
3.四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是(
??)
A.?平行四边形???B.?矩形???C.?菱形??D.?正方形
4.如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形是一个特殊的四边形.
(1)这个特殊的四边形应该叫做________;
(2)请证明你的结论.
如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE.求证:四边形BCED是菱形.
如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E.
求证:四边形ADEF是菱形.
如图,在?ABCD中,O为AC的中点,过点O作EF⊥AC与边AD、BC分别相交于点E、F,求证:四边形AECF是菱形.
【菱形的有关计算】
1、菱形的周长=4×边长
2、菱形的面积=底×高=对角线乘积的一半
温馨提示
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
1.如图所示,在菱形ABCD中,AC=8,BD=10.求:(1)AB的长.(2)菱形ABCD的面积.
2.如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,AD=7,BF=6,则四边形ABEF的面积为(??
)
A.?48?????????????????????????????????????????B.?35?????????????????????????????????????????C.?30?????????????????????????????????????????D.?24
3.若菱形
的周长是16,
∠A=60°
,则对角线
的长度为(
)
A.?2????????????????????????????????????????B.?????????????????????????????????????????C.?4????????????????????????????????????????D.?
4.下列说法中,错误的是(??
)
A.平行四边形的对角线互相平分
B.对角线互相垂直的四边形是菱形
C.菱形的对角线互相垂直
D.对角线互相平分的四边形是平行四边形
5.如图,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作P点到直线AB,AD的垂线段PE,PF,则PE+PF等于(??
)
A.?6??B.?3????C.?1.5??????D.?0.75
6.如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿
CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,求t的值
7.如图,在四边形
中,
,点
E
是
边的中点.点
F
恰是点
E
关于
所在直线的对称点.
(1)证明:四边形
为菱形;
(2)连接
交
于点
O
.若
,求线段
的长.
8.如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.
9.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
【课后练习】
1.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2
,则CE的长为________
第1题
第2题
第3题
第4题
2.如图,点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=________度.
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABC的周长是________.
4.如图,菱形ABC的对角线相交于点O,过点D作DE∥AC,且DE=
AC,连接CE、OE、AE,AE交OD于点F,若AB=2,∠ABC=60°,则AE的长________.
5.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形
中,
,
,则
的长为________.
6.如图:在△ABC中,∠BAC
=
,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
7.如图,在平行四边形
中,∠BAD的平分线交
于E,点
F
在
上,且
,连接
.
(1)判断四边形
的形状并证明;
(2)若
、
相交于点
O
,且四边形
的周长为
,
,求
的长度及四边形
的面积.
8.如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
9.如图:菱形的边长为,,对角线、相交于,求菱形的面积.
?
10.已知菱形的周长为,两个相邻对角之比为,求它的对角线长和面积.
11.如图,在中,,平分,于点,与交于点,.
求证:与互相垂直平分.
?
12.如图,在中,是的角平分线,,,交于点,请问是的角平分线吗?请说明理由.
答案
【菱形的性质】
1.A
2.
3.B
4.A
5.B
6.∵四边形ABCD是菱形,∴∠A=∠C,AD=CD,又∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°,
在△ADE和△CDF中,
,∴△ADE≌△CDF(AAS).
7.(1)证明:
∵
四边形ABCD是平行四边形,
,且
,
,
,
,四边形AECF是平行四边形.
(2)如图,∵四边形AECF是菱形,∴AE=EC,∴∠1=∠2,∵∠BAC=90°,
∴∠3=90°-∠2,∠4=90°-∠1,∴∠3=∠4∴AE=BE,∴
BE=AE=CE=BC=5
8.(1)证明:∵四边形ABCD是菱形,∴AO=CO,AB∥CD,∴∠EAO=∠FCO,∠AEO=∠CFO.
在△OAE和△OCF中,∠EAO=∠FCO,AO=CO,∠AEO=∠CFO,∴△AOE≌△COF,∴AE=CF;
解:∵E是AB中点,∴BE=AE=CF.∵BE∥CF,∴四边形BEFC是平行四边形,∵AB=2,∴EF=BC=AB=2.
【菱形的判定】
1.×
√
×
×
2.D
3.C
4.(1)菱形;(2)∵四边形是用两张等宽的纸条交叉重叠地放在一起而组成的图形,∴,,
∴四边形是平行四边形(对边相互平行的四边形是平行四边形);
过点分别作,边上的高为,.则(两纸条相同,纸条宽度相同);
∵平行四边形中,,即,∴.∴平行四边形为菱形
5.证明:∵
≌
,∴
?,在
和
中
,
∴
≌
?,∴
,又∵
,∴
?,∴
,
∴
,∴
,∴四边形BCED是菱形.
6.由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA∵四边形ABCD是平行四边形∴DE∥AF∴∠DEA=∠EAF
∴∠EAF=∠FEA∴AF=EF????∴AF=AD=DE=EF∴四边形ADEF是菱形.
7.
∵四边形ABCD是平行四边形,∴BC∥AD,∴AE∥CF,∴∠OAE=∠OCF,∵点O是AC的中点,∴OA=OC,
在△AOE和△COF中,
?∴△AOE≌△COF(ASA),∴AE=CF,∵AE∥CF,
∴四边形AECF是平行四边形,∵EF与AC垂直,∴四边形AECF是菱形
【菱形的有关计算】
1.(1)∵
四边形ABCD是菱形.∴
AC⊥BD,AO=AC,OB=BD.
又∵
AC=8,BD=10.
∴
AO=×8=4,OB=×10=5.在Rt△ABO中,∴
,∴
.
(2)由菱形的性质可知:
2.D
3.C
4.B
5.B
6.由题意CD=4t,AE=2t,
∵DF⊥BC于F,∴∠DFC=90°在Rt△DFC中,∵∠C=30°,
∴DF=
CD=2t,∴DF=AE,∵∠CFD=∠B=90°,∴DF∥CE,∴四边形DFEA是平行四边形,
∴当DF=AD时,四边形DFEA是菱形.∴120﹣4t=2t,∴t=20s,∴t=20s时,四边形DFEA是菱形.
7.(1)证明:
,点E是AB变的中点
点F恰是点E关于AC所在直线的对称点
四边形
为菱形
(2)解:∵四边形
是菱形,∴
,∴
,∴
8.(1)∵CE∥DB,BE∥DC,∴四边形DBEC为平行四边形.又∵Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴CD=BD=
AC,∴平行四边形DBEC是菱形
(2)解:∵点D,F分别是AC,AB的中点,AD=3,DF=1,∴DF是△ABC的中位线,AC=2AD=6,S△BCD=
S△ABC
∴BC=2DF=2.又∵∠ABC=90°,∴AB=
=
=4
.
∵平行四边形DBEC是菱形,∴S四边形DBEC=2S△BCD=S△ABC=
AB?BC=
×4
×2=4
9.(1)∵AB=AC,AD⊥BC,∴D为BC的中点.∵E、F分别为AB、AC的中点,∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,∴四边形AEDF是平行四边形.∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF,∴四边形AEDF是菱形
(2)解:∵EF为△ABC的中位线,∴EF=
BC=5.∵AD=8,AD⊥EF,∴S菱形AEDF=
AD?EF=
×8×5=20
(3)解:∵EF∥BC,∴EH∥BP.若四边形BPHE为平行四边形,则须EH=BP,∴5﹣2t=3t,解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形.∵EF∥BC,∴FH∥PC.
若四边形PCFH为平行四边形,则须FH=PC,∴2t=10﹣3t,解得:t=2,∴当t=2秒时,四边形PCFH为平行四边形
【课后练习】
1.
5
或
2.45
3.18
4.
5.
6.∵AD⊥BC,∴∠ADB=90°,∵∠BAC=90°,∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,∴∠B=∠CAD,
∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA),∴AE=EF(角平分线上的点到角两边的距离相等),
∵CE=CE,∴由勾股定理得:AC=CF,∵△ACG和△FCG中
?∴△ACG≌△FCG,∴∠CAD=∠CFG,∵∠B=∠CAD∴∠B=∠CFG,∴GF∥AB,∵AD⊥BC,EF⊥BC,∴AD∥EF,即AG∥EF,AE∥GF,
∴四边形AEFG是平行四边形,∵AE=EF,∴平行四边形AEFG是菱形.
7.(1)解:∵AE是∠BAF的角平分线,∴∠BAE=∠FAE,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠FAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE.∵AB=AF,∴BE=FA,∴四边形ABEF为平行四边形,∵AB=AF,∴四边形ABEF为菱形
(2)解:∵四边形ABEF为菱形,且周长为20,∴AB=5,AE⊥BF,BO=
FB=3,AE=2AO,
在Rt△AOB中,AO=
=4,∴AE=2AO=8,菱形ABEF面积=
AE×BF=
×8×6=24
8.(1)证明:∵在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,
∴AO=AC=3,BO=BD=4,∵AB=5,且32+42=52,∴AO2+BO2=AB2,
∴△AOB是直角三角形,且∠AOB=90°,
∴AC⊥BD,∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴BC=AB=5,∵S△ABC=AC?BO=BC?AH,
∴×6×4=×5×AH,解得:AH=.
9.:在菱形中,又在中,,∴,
,∴为等边三角形∴.
在菱形中,,∴为直角三角形,∴,
∴,∴,∴.
10.解:∵菱形的周长为,∴菱形的边长,∵两个相邻对角之比为,
∴,∴是等边三角形,∴,∵菱形对角线,∴,∴,∴菱形的面积.
11.:延长交于点.∵,,∴,即.
又∵,平分,∴.在与中,,∴,
∴.在与中,,∴,∴,
∴垂直平分(三合一).∴,在与中,,∴
∴,又∵.∴四边形为平行四边形,∵,∴四边形为菱形,∴与互相垂直平分.
12.解:是的角平分线,理由是:∵,,∴四边形是平行四边形,
∵,∴,∵是的角平分线,∴,
∴,∴,∴四边形是菱形,∴平分,即是的角平分线.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
