鲁教版数学七年级上册期末测试题(二)(含答案)
文档属性
| 名称 | 鲁教版数学七年级上册期末测试题(二)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 08:07:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
鲁教版数学七年级上册期末测试题(二)
(时间:100分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
2.如图,一束光线从点A(4,4)出发,经y轴上的点C反射后经过点B(1,0),则点C的坐标是( )
A.(0,) B.(0,) C.(0,1) D.(0,2)
3.如图,点A,E,F,D在同一直线上,若AB∥CD,AB=CD,AE=FD,则图中的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.已知三角形三个内角∠A,∠B,∠C,满足关系式∠B+∠C=2∠A,则此三角形( )
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
5.在平面直角坐标系中,一次函数y=x-1的图象是( )
6.如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=2,过点C作CD⊥AB,垂足为点D,则CD的长为( )
A. B. C.1 D.2
7.下列等式成立的是( )
A.=±1 B.=15 C.=-9 D.=-3
8.在Rt△ABC中,∠C=90°,∠A=30°,边AC的垂直平分线DE交AB于点D,垂足为点E,若DE=2,则BD的长为( )
A.1 B.2 C.3 D.4
9.如图,∥m,等边△ABC的顶点B在直线m上,∠1=20°,则∠2的度数为.( )
A.60° B.45° C.40° D.30°
10.若=(x+y)2,则x-y的值为( )
A.-1 B.1 C.2 D.3
11.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
12.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是( )
A.(5,30) B.(8,10) C.(9,10) D.(10,10)
二、填空题(每小题4分,共24分)
13.的立方根是___________。
14.若a,b,c为三角形的三边长,且a,b满足|a-3|+(b-2)2=0,则第三边长c的取值范围是______________。
15.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(a,b),则a与b的数量关系为______________。
16.如图,在△ABC中,AB=AC,∠C=72°,BC=,以点B为圆心,BC为半径画弧,交AC于点D,则线段AD的长为____________。
17.如图,在△ABC中,∠ACB=120°,BC=4,DC=2,D为AB的中点,DC⊥BC,则△ABC的面积是____________。
18.如图,是按一定规律排成的三角形数阵,按图中的数阵排列规律,第9行从左至右第5个数是__________。
1
2
3
……
三、解答题(19-20每题10分,21题11分,22-23每题10分,24题13分,25题14分,共78分)
19.(1)计算:.
(2)计算:(。
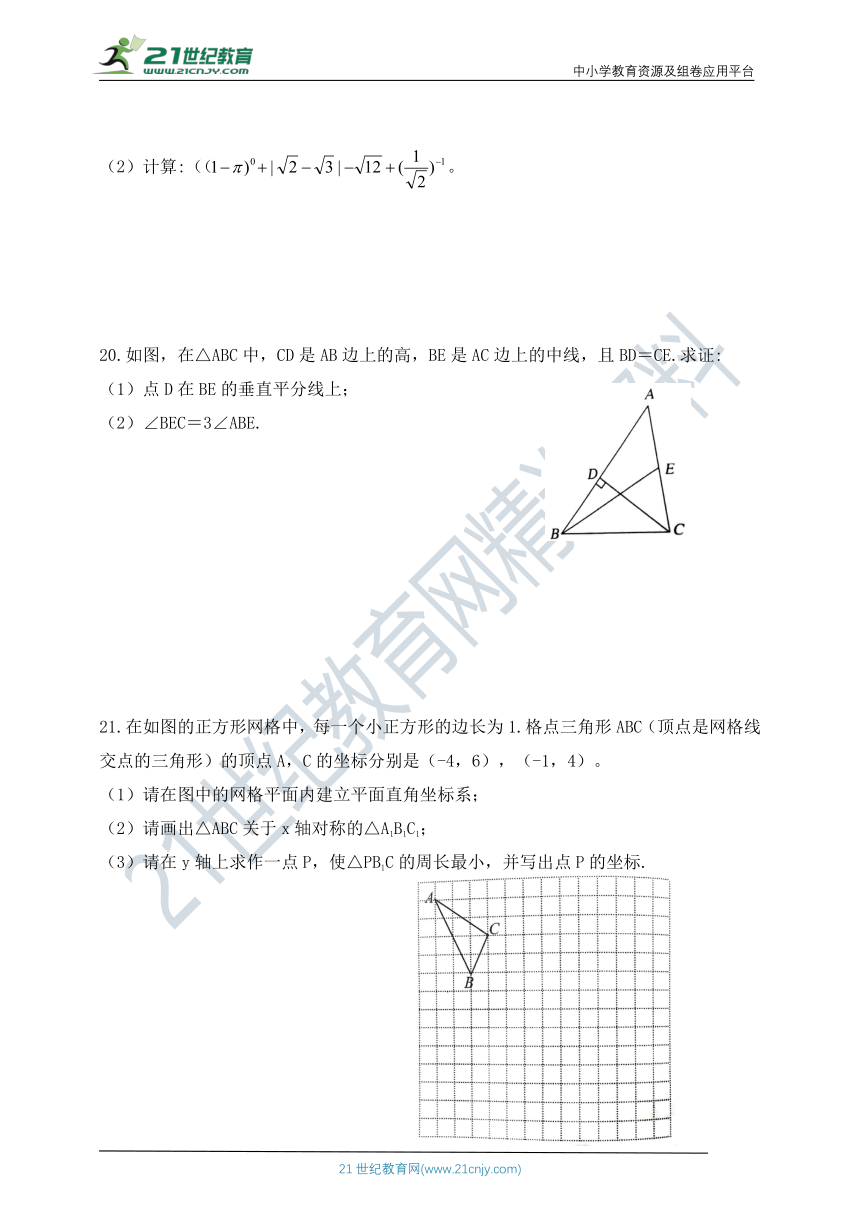
20.如图,在△ABC中,CD是AB边上的高,BE是AC边上的中线,且BD=CE.求证:
(1)点D在BE的垂直平分线上;
(2)∠BEC=3∠ABE.
21.在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别是(-4,6),(-1,4)。
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
22.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上,若AB=2,求CD的长。
23.如图,在四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点E从A点出发,以2cm/s的速度向B点移动,设移动的时间为 x S.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由。
24.如图,在直角坐标系xOy中,一次函数y=-x+5的图象1分别与x,y轴交于A,B两点,正比例函数的图象2与1交于点C(m,4)。
(1)求m的值及2的表达式;
(2)求S△AOC-S△BOC的值;
(3)一次函数y=kx+1的图象为3,且1,2,3不能围成三角形,直接写出k的值.
25.如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A,B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC-CB的方向运动,当点P与点B重合时停止运动,运动时间为ts.
(1)当点P经过点C时,求直线DP的函数表达式;
(2)①求△OPD的面积S关于t的函数表达式;
②如图②,把长方形沿着OP折叠,点B的对应点B恰好落在AC边上,求点P的坐标;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
参考答案
一、选择题
1.C 2.B 3.C 4.B 5.B 6.C 7.C 8.D 9.C
10.C 11.D 12.C
二、填空题
13.2 14.1三、解答题
19.解:(1)原式=1+-1-+3=3.
(2)原式=1+--2+=1-.
20.解:(1)如图,连接DE.因为CD是AB边上的高,所以∠ADC=∠BDC=90°.
因为BE是AC边上的中线,所以AE=CE.所以DE=CE.
因为BD=CE,所以BD=DE,所以点D在BE的垂直平分线上.
(2)因为DE=AE,所以∠A=∠ADE.
因为∠ADE=∠DBE+∠DEB.且BD=DE,所以∠DBE=∠DEB.
所以∠A=∠ADE=2∠ABE,因为∠BEC=∠A+∠ABE,所以∠BEC=3∠ABE。
21.解:(1)如图所示;
(2)如图所示;
(3)如图,作点1关于y轴的对称点B2,连接B2C交y轴于点P,则点P为所求,点P的坐标是(0,2)。
22.解:如图,过点A作AF⊥BC于点F,在Rt△ABC中,∠B=45,
所以BC=AB=2,BF=AF=BC=AB=。
因为两个同样大小的含45?角的三角尺,所以AD=BC=2。
在Rt△ADF中,根据勾股定理得DF==。
所以CD=BF+DF=BC=+-2=-。
23.解:(1)当x=5时,点E在线段CD的垂直平分线上,
理由是:当x=5时,AE=2×5=10=BC.因为AB=25cm,DA=15cm,CB=10cm,
所以BE=AD=15cm。
在△ADE和△BEC中,因为,所以△ADE≌△BEC(SAS),所以DE=CE.
所以点E在线段CD的垂直平分线上分线上,即当x=5时,点E在线段CD的垂直平分线上。
(2)DE与CE的位置关系是DE⊥CE。
理由是:因为△ADE≌△BEC,所以∠ADE=∠BEC。
因为∠A=90°,所以∠ADE+∠AED=90°,所以∠AED+∠CEB=90°。
所以∠DEC=180°-(∠AED+∠CEB)=90°,所以DE⊥CE。
24.解:(1)把C(m,4)代入一次函数y=-x+5,可得4=-m+5,解得m=2.
所以点C的坐标为(2,4)。
设2的表达式为y=ax,则有4=2a,解得a=2.所以2的表达式为y=2x。
(2)如图,过点C作CD⊥AO于点D,CE⊥BO于点E,则CD=4,CE=2.
当x=0时,y=-x+5=5;
当y=0时,-x+5=0,解得x=10
所以点A的坐标为(10,0),点B的坐标为(0,5)所以AO=10,BO=5.
所以S△AOC-S△BOC=×10×4-×5×2=20-5=15。
(3)因为一次函数y=kx+1的图象为3,且1,2,3不能围成三角形,
所以当3经过点C(2,4)时,有4=2k+1,解得k=;
当2,3平行时,k=2;当1,3平行时,k=-.
故k的值为或2或-.
25.解:(1)因为OA=6,OB=10,四边形OACB为长方形,所以点C的坐标为(6,10).
设此时直线DP的表达式为y=kx+b,把(0,2),C(6,10)分别代入,得,
解得,则此时直线DP的表达式为y=x+2。
(2)①当点P在线段AC上时,OD=2,高为6,S=6;
当点P在线段BC上时,OD=2,高为6+10-2t=16-2t,
则S=×2×(16-2t)=-2t+16.
②设P(m,10),则PB=PB=m,因为OB'=OB=10,OA=6,
所以AB′==8。所以B'C=10-8=2。
因为PC=6-m,所以m2=22+(6-m)2,解得m=。
则此时点P的坐标是(,10)。
(3)存在,理由如下:
若△BDP为等腰三角形,分三种情况考虑:如图,
①当BD=BP1=OB-OD=10-2=8时,在Rt△BCP1中,BP1=8,BC=6,
根据勾股定理得CP1==2。所以AP1=10-2,即P1(6,10-2);
②当BP2=DP2时,此时P2(6,6);
③当DB=DP3=8时,在Rt△DEP3中,DE=6,
根据勾股定理得P3E==2。
所以AP3=AE+EP3=2+2,即P3(6,2+2)。
综上,满足题意的点P的坐标为(6,6)或(6,2+2)或(6,10-2)。
_21?????????è?????(www.21cnjy.com)_
鲁教版数学七年级上册期末测试题(二)
(时间:100分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
2.如图,一束光线从点A(4,4)出发,经y轴上的点C反射后经过点B(1,0),则点C的坐标是( )
A.(0,) B.(0,) C.(0,1) D.(0,2)
3.如图,点A,E,F,D在同一直线上,若AB∥CD,AB=CD,AE=FD,则图中的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.已知三角形三个内角∠A,∠B,∠C,满足关系式∠B+∠C=2∠A,则此三角形( )
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
5.在平面直角坐标系中,一次函数y=x-1的图象是( )
6.如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=2,过点C作CD⊥AB,垂足为点D,则CD的长为( )
A. B. C.1 D.2
7.下列等式成立的是( )
A.=±1 B.=15 C.=-9 D.=-3
8.在Rt△ABC中,∠C=90°,∠A=30°,边AC的垂直平分线DE交AB于点D,垂足为点E,若DE=2,则BD的长为( )
A.1 B.2 C.3 D.4
9.如图,∥m,等边△ABC的顶点B在直线m上,∠1=20°,则∠2的度数为.( )
A.60° B.45° C.40° D.30°
10.若=(x+y)2,则x-y的值为( )
A.-1 B.1 C.2 D.3
11.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
12.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是( )
A.(5,30) B.(8,10) C.(9,10) D.(10,10)
二、填空题(每小题4分,共24分)
13.的立方根是___________。
14.若a,b,c为三角形的三边长,且a,b满足|a-3|+(b-2)2=0,则第三边长c的取值范围是______________。
15.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(a,b),则a与b的数量关系为______________。
16.如图,在△ABC中,AB=AC,∠C=72°,BC=,以点B为圆心,BC为半径画弧,交AC于点D,则线段AD的长为____________。
17.如图,在△ABC中,∠ACB=120°,BC=4,DC=2,D为AB的中点,DC⊥BC,则△ABC的面积是____________。
18.如图,是按一定规律排成的三角形数阵,按图中的数阵排列规律,第9行从左至右第5个数是__________。
1
2
3
……
三、解答题(19-20每题10分,21题11分,22-23每题10分,24题13分,25题14分,共78分)
19.(1)计算:.
(2)计算:(。
20.如图,在△ABC中,CD是AB边上的高,BE是AC边上的中线,且BD=CE.求证:
(1)点D在BE的垂直平分线上;
(2)∠BEC=3∠ABE.
21.在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别是(-4,6),(-1,4)。
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
22.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上,若AB=2,求CD的长。
23.如图,在四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点E从A点出发,以2cm/s的速度向B点移动,设移动的时间为 x S.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由。
24.如图,在直角坐标系xOy中,一次函数y=-x+5的图象1分别与x,y轴交于A,B两点,正比例函数的图象2与1交于点C(m,4)。
(1)求m的值及2的表达式;
(2)求S△AOC-S△BOC的值;
(3)一次函数y=kx+1的图象为3,且1,2,3不能围成三角形,直接写出k的值.
25.如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A,B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC-CB的方向运动,当点P与点B重合时停止运动,运动时间为ts.
(1)当点P经过点C时,求直线DP的函数表达式;
(2)①求△OPD的面积S关于t的函数表达式;
②如图②,把长方形沿着OP折叠,点B的对应点B恰好落在AC边上,求点P的坐标;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
参考答案
一、选择题
1.C 2.B 3.C 4.B 5.B 6.C 7.C 8.D 9.C
10.C 11.D 12.C
二、填空题
13.2 14.1
19.解:(1)原式=1+-1-+3=3.
(2)原式=1+--2+=1-.
20.解:(1)如图,连接DE.因为CD是AB边上的高,所以∠ADC=∠BDC=90°.
因为BE是AC边上的中线,所以AE=CE.所以DE=CE.
因为BD=CE,所以BD=DE,所以点D在BE的垂直平分线上.
(2)因为DE=AE,所以∠A=∠ADE.
因为∠ADE=∠DBE+∠DEB.且BD=DE,所以∠DBE=∠DEB.
所以∠A=∠ADE=2∠ABE,因为∠BEC=∠A+∠ABE,所以∠BEC=3∠ABE。
21.解:(1)如图所示;
(2)如图所示;
(3)如图,作点1关于y轴的对称点B2,连接B2C交y轴于点P,则点P为所求,点P的坐标是(0,2)。
22.解:如图,过点A作AF⊥BC于点F,在Rt△ABC中,∠B=45,
所以BC=AB=2,BF=AF=BC=AB=。
因为两个同样大小的含45?角的三角尺,所以AD=BC=2。
在Rt△ADF中,根据勾股定理得DF==。
所以CD=BF+DF=BC=+-2=-。
23.解:(1)当x=5时,点E在线段CD的垂直平分线上,
理由是:当x=5时,AE=2×5=10=BC.因为AB=25cm,DA=15cm,CB=10cm,
所以BE=AD=15cm。
在△ADE和△BEC中,因为,所以△ADE≌△BEC(SAS),所以DE=CE.
所以点E在线段CD的垂直平分线上分线上,即当x=5时,点E在线段CD的垂直平分线上。
(2)DE与CE的位置关系是DE⊥CE。
理由是:因为△ADE≌△BEC,所以∠ADE=∠BEC。
因为∠A=90°,所以∠ADE+∠AED=90°,所以∠AED+∠CEB=90°。
所以∠DEC=180°-(∠AED+∠CEB)=90°,所以DE⊥CE。
24.解:(1)把C(m,4)代入一次函数y=-x+5,可得4=-m+5,解得m=2.
所以点C的坐标为(2,4)。
设2的表达式为y=ax,则有4=2a,解得a=2.所以2的表达式为y=2x。
(2)如图,过点C作CD⊥AO于点D,CE⊥BO于点E,则CD=4,CE=2.
当x=0时,y=-x+5=5;
当y=0时,-x+5=0,解得x=10
所以点A的坐标为(10,0),点B的坐标为(0,5)所以AO=10,BO=5.
所以S△AOC-S△BOC=×10×4-×5×2=20-5=15。
(3)因为一次函数y=kx+1的图象为3,且1,2,3不能围成三角形,
所以当3经过点C(2,4)时,有4=2k+1,解得k=;
当2,3平行时,k=2;当1,3平行时,k=-.
故k的值为或2或-.
25.解:(1)因为OA=6,OB=10,四边形OACB为长方形,所以点C的坐标为(6,10).
设此时直线DP的表达式为y=kx+b,把(0,2),C(6,10)分别代入,得,
解得,则此时直线DP的表达式为y=x+2。
(2)①当点P在线段AC上时,OD=2,高为6,S=6;
当点P在线段BC上时,OD=2,高为6+10-2t=16-2t,
则S=×2×(16-2t)=-2t+16.
②设P(m,10),则PB=PB=m,因为OB'=OB=10,OA=6,
所以AB′==8。所以B'C=10-8=2。
因为PC=6-m,所以m2=22+(6-m)2,解得m=。
则此时点P的坐标是(,10)。
(3)存在,理由如下:
若△BDP为等腰三角形,分三种情况考虑:如图,
①当BD=BP1=OB-OD=10-2=8时,在Rt△BCP1中,BP1=8,BC=6,
根据勾股定理得CP1==2。所以AP1=10-2,即P1(6,10-2);
②当BP2=DP2时,此时P2(6,6);
③当DB=DP3=8时,在Rt△DEP3中,DE=6,
根据勾股定理得P3E==2。
所以AP3=AE+EP3=2+2,即P3(6,2+2)。
综上,满足题意的点P的坐标为(6,6)或(6,2+2)或(6,10-2)。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
