北师大版七年级数学上册单元练习第四章基本平面图形(word版含解析)
文档属性
| 名称 | 北师大版七年级数学上册单元练习第四章基本平面图形(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 258.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览




文档简介
第四章基本平面图形
一、选择题
(2019·上海松江区·期末)如图,四条表示方向的射线,表示北偏东
的是
A.
B.
C.
D.
(2019·广州市黄埔区·模拟)如图,在正方形
中,,
是对角线
上的两个动点,
是正方形四边上的任意一点,且
,,设
,在下列关于
是等腰三角形和对应
点个数的说法中,
①当
(即
,
两点重合)时,
点有
个;
②当
点有
个时,;
③当
是等边三角形时,
点有
个;
④当
时,
点最多有
个.
其中结论正确的是
A.①②
B.①③
C.②③
D.③④
(2019·宁波市镇海区)在直线
上且到
轴或
轴距离为
的点有
A.
个
B.
个
C.
个
D.
个
(2019·石家庄市桥西区)点
,,
在同一直线上,已知
,,则线段
的长是
A.
B.
C.
D.
或
(2019·深圳市龙岗区)已知
,,
都是非零有理数,满足
,令
,则
的值为
A.
B.
C.
D.
(2019·杭州市余杭区·模拟)蜂巢的构造非常美丽、科学,如图是由
个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,
的顶点都在格点上.设定
边如图所示,则
是直角三角形的个数有
A.
个
B.
个
C.
个
D.
个
(2019·东莞市莞城区·模拟)如图,在平行四边形
中,,,,点
从点
出发沿着
的路径运动,同时点
从点
出发沿着
的路径以相同的速度运动,当点
到达点
时,点
随之停止运动,设点
运动的路程为
,,下列图象中大致反映
与
之间的函数关系的是
A.
B.
C.
D.
(2019·天津南开区·期末)
中,
厘米,,
厘米,点
为
的中点.如果点
在线段
上以
厘米/秒的速度由
点向
点运动,同时,点
在线段
上由
点向
点运动.若点
的运动速度为
厘米/秒,则当
与
全等时,
的值为
A.
B.
C.
或
D.
或
(2019·淮安市淮阴区·期末)点
在线段
上,下列条件中不能确定点
是线段
中点的是
A.
B.
C.
D.
(2019·哈尔滨市香坊区·期末)下列说法中,正确的有
个.
①如果
,那么
,;
②用圆规画圆时,若圆规两脚间的距离是
,则所画圆的半径为
;
③小红身高
米,老师身高
厘米,小红和老师身高的比是
;
④用四个圆心角都是
的扇形,一定可以拼成一个圆;
⑤圆锥体积等于圆柱体积的
.
A.
B.
C.
D.
(2018·拉萨市城关区·期末)设
是自然数,则
的值为
A.
或
B.
C.
D.
或
(2019·长春市朝阳区)已知等腰三角形的两边长
,
满足方程组
则此等腰三角形的周长为
A.
B.
C.
D.
或
(2019·济南市章丘区·期末)如图,
是直线
上一点,
平分
,,若
,则
为
A.
B.
C.
D.
二、填空题
(2019·海口市琼山区·期末)已知线段
和
在同一直线上,如果
,,则线段
和
的中点之间的距离为
.
(2018·无锡市梁溪区·期末)已知
,以
为顶点作射线
,若
,则
.
(2019·滨州市滨城区·期末)已知点
,点
,点
在同一条直线上,,,
为
的中点,则
,
.
(2020·上海·期末)时针从钟面上
点旋转到
点,共旋转了
.
(2018·无锡市滨湖区·期末)记抛物线
:
的顶点为
,抛物线
:
顶点是点
,且与
轴的正半轴交于点
.当
是直角三角形时,抛物线
的解析式为
.
(2019·杭州市拱墅区·期末)已知点
,,
都在直线
上,点
是线段
的中点,设
,,则线段
的长为
.(用含
,
的代数式表示)
三、解答题
(2018·广州市白云区·期末)在平面内有四点,,,,,如图,请用直尺和圆规作图完成.(不写作法,保留画图痕迹).
()画直线
.
()画射线
与直线
交于
.
()连接
并延长
到
,使
.
()在线段
上找的一点
,使
的值最小.
(2020·上海·专项)钟面上从
点到
点有几次时针与分针夹成
的角?分别是几点几分?
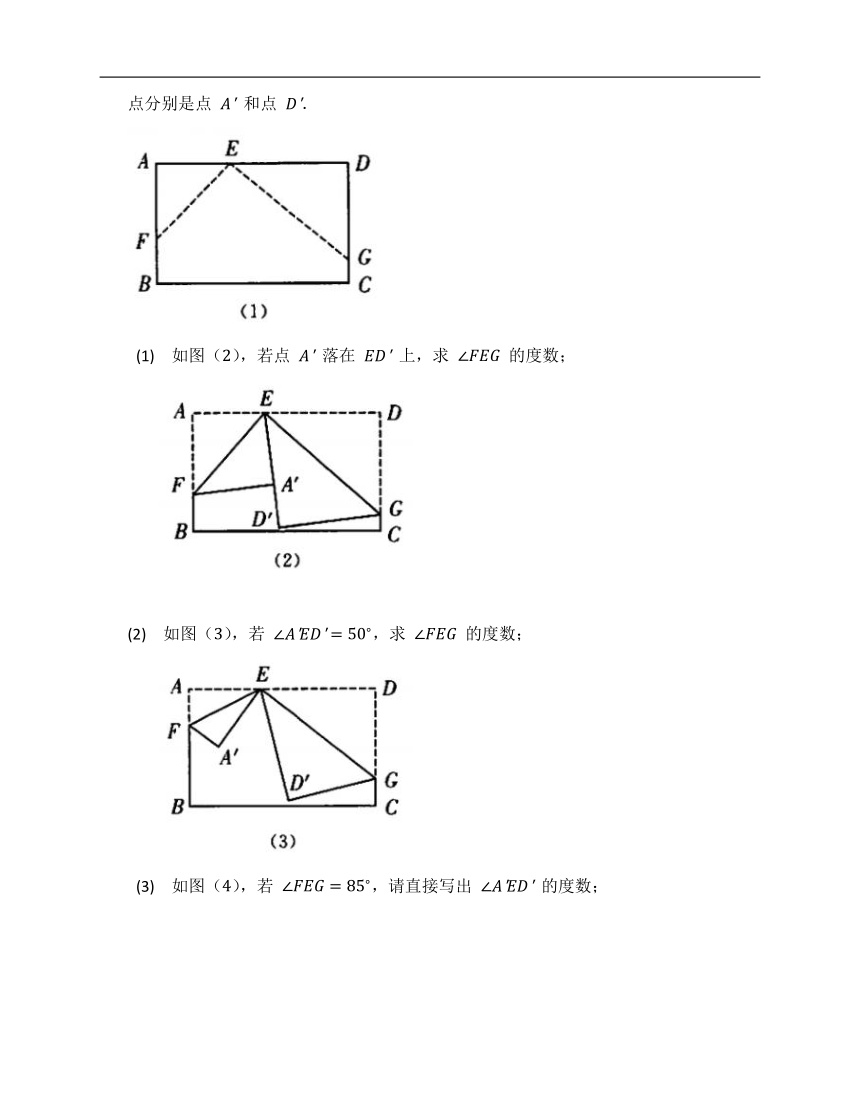
(2020·单元测试)如图(),在长方形纸片
中,点
在边
上,点
,
分别在边
,
上,分别以
,
为折痕进行折叠并压平,点
,
的对应点分别是点
和点
.
(1)
如图(),若点
落在
上,求
的度数;
(2)
如图(),若
,求
的度数;
(3)
如图(),若
,请直接写出
的度数;
(4)
若
,直接写出
的度数(用含
的代数式表示).
第四章基本平面图形
一、选择题
(2019·上海松江区·期末)如图,四条表示方向的射线,表示北偏东
的是
A.
B.
C.
D.
【答案】B
【知识点】方向角
(2019·广州市黄埔区·模拟)如图,在正方形
中,,
是对角线
上的两个动点,
是正方形四边上的任意一点,且
,,设
,在下列关于
是等腰三角形和对应
点个数的说法中,
①当
(即
,
两点重合)时,
点有
个;
②当
点有
个时,;
③当
是等边三角形时,
点有
个;
④当
时,
点最多有
个.
其中结论正确的是
A.①②
B.①③
C.②③
D.③④
【答案】B
【解析】①如图,当
(即
,
两点重合)时,
点有
个,故正确;
②当
点有
个时,当
或
或
或
时,
点有
个,故错误;
③如图,当
是等边三角形时,
点有
个,故正确;
④当
时,
点最多有
个,故错误.
【知识点】正方形的性质、圆周角定理推论、等腰三角形的性质
(2019·宁波市镇海区)在直线
上且到
轴或
轴距离为
的点有
A.
个
B.
个
C.
个
D.
个
【答案】C
【解析】距离
轴距离为
的点,定在直线
或
上,
令
得
,
为
,
令
得
,
为
,
距离
轴距离为
的点,定在直线
或
上,
令
,得
,
为
,
令
,得
,
为
,
有重合两点,
共有
,,
三点.
【知识点】一次函数图像上点的坐标特征
(2019·石家庄市桥西区)点
,,
在同一直线上,已知
,,则线段
的长是
A.
B.
C.
D.
或
【答案】D
【解析】当点
在线段
上时,
,,
,
当点
在线段
的延长线上时,
,,
.
【知识点】线段的和差
(2019·深圳市龙岗区)已知
,,
都是非零有理数,满足
,令
,则
的值为
A.
B.
C.
D.
【答案】B
【解析】①当
,,
为两正一负时:,
,则
;
②当
,,
为两负一正时:,,
则
;
由①②知则
的所有可能的值为
.
故选B.
【知识点】简单的代数式求值
(2019·杭州市余杭区·模拟)蜂巢的构造非常美丽、科学,如图是由
个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,
的顶点都在格点上.设定
边如图所示,则
是直角三角形的个数有
A.
个
B.
个
C.
个
D.
个
【答案】D
【解析】如图,
是直角边时,点
共有
个位置,即有
个直角三角形;
是斜边时,点
共有
个位置,即有
个直角三角形,
综上所述,
是直角三角形的个数有
个.
【知识点】直角三角形的性质与判定、多边形的相关概念
(2019·东莞市莞城区·模拟)如图,在平行四边形
中,,,,点
从点
出发沿着
的路径运动,同时点
从点
出发沿着
的路径以相同的速度运动,当点
到达点
时,点
随之停止运动,设点
运动的路程为
,,下列图象中大致反映
与
之间的函数关系的是
A.
B.
C.
D.
【答案】B
【解析】在
中,,,,
.
当
时,,,
;
当
时,,,
;
当
时,,,
.
【知识点】分段函数、y=ax^2+bx+c的图象
(2019·天津南开区·期末)
中,
厘米,,
厘米,点
为
的中点.如果点
在线段
上以
厘米/秒的速度由
点向
点运动,同时,点
在线段
上由
点向
点运动.若点
的运动速度为
厘米/秒,则当
与
全等时,
的值为
A.
B.
C.
或
D.
或
【答案】D
【解析】当
时,
与
全等,
点
为
的中点,
,
,
,
点
在线段
上以
厘米/秒的速度由
点向
点运动,
运动时间时
,
,
,
;
当
时,,
,,
,
,
,
运动时间为
,
.
故
的值为
或
.
【知识点】边角边
(2019·淮安市淮阴区·期末)点
在线段
上,下列条件中不能确定点
是线段
中点的是
A.
B.
C.
D.
【答案】B
【解析】A、
,则点
是线段
中点;
B、
,则
可以是线段
上任意一点;
C、
,则点
是线段
中点;
D、
,则点
是线段
中点.
【知识点】线段的和差
(2019·哈尔滨市香坊区·期末)下列说法中,正确的有
个.
①如果
,那么
,;
②用圆规画圆时,若圆规两脚间的距离是
,则所画圆的半径为
;
③小红身高
米,老师身高
厘米,小红和老师身高的比是
;
④用四个圆心角都是
的扇形,一定可以拼成一个圆;
⑤圆锥体积等于圆柱体积的
.
A.
B.
C.
D.
【答案】B
【解析】①如果
,那么
,
或
,
等,本说法错误;
②用圆规画圆时,若圆规两脚间的距离是
,则所画圆的半径为
,本说法正确;
③小红身高
米,即
厘米,老师身高
厘米,
小红和老师身高的比是
,即
,本说法正确;
④用四个圆心角都是
、半径相等的扇形,一定可以拼成一个圆,当半径不相等时,不能拼成一个圆,本说法错误;
⑤底面积相等、高相等时,圆锥体积等于圆柱体积的
,如果不确定底面积相等、高相等,圆锥体积不一定等于圆柱体积的
,本说法错误.
【知识点】圆的定义
(2018·拉萨市城关区·期末)设
是自然数,则
的值为
A.
或
B.
C.
D.
或
【答案】A
【解析】因为
为自然数,且
与
是两个整数,所以
与
必定同是偶数,或同是奇数;
又因为
的奇数次幂是
,
的偶数次幂是
,
所以,若
和
同为偶数,则
;若
和
同为奇数,则
.
【知识点】有理数的乘方
(2019·长春市朝阳区)已知等腰三角形的两边长
,
满足方程组
则此等腰三角形的周长为
A.
B.
C.
D.
或
【答案】A
【解析】
解不等式组可得
等腰三角形的两边长为
,,
三边可能情况为
,,
或
,,,
,,
不能构成三角形,
等腰三角形的周长为
.
【知识点】等腰三角形的概念
(2019·济南市章丘区·期末)如图,
是直线
上一点,
平分
,,若
,则
为
A.
B.
C.
D.
【答案】B
【解析】
,
,
平分
,
,
,
.
【知识点】角的计算、角平分线的定义
二、填空题
(2019·海口市琼山区·期末)已知线段
和
在同一直线上,如果
,,则线段
和
的中点之间的距离为
.
【答案】
或
【解析】此题有两种情况:
①当
点在线段
上,此时
,
而
,.
,
线段
和
的中点之间的距离为:
;
②当
点在线段
上,此时
,
而
,.
,
线段
和
的中点之间的距离为:
.
【知识点】线段的和差、线段中点的概念及计算
(2018·无锡市梁溪区·期末)已知
,以
为顶点作射线
,若
,则
.
【答案】
或
【解析】
,,
,
当
在
下方时,;
当
在
上方时,.
故答案为:
或
.
【知识点】角的计算
(2019·滨州市滨城区·期末)已知点
,点
,点
在同一条直线上,,,
为
的中点,则
,
.
【答案】
或
;
或
【知识点】线段中点的概念及计算、线段的和差
(2020·上海·期末)时针从钟面上
点旋转到
点,共旋转了
.
【答案】
【知识点】钟面角
(2018·无锡市滨湖区·期末)记抛物线
:
的顶点为
,抛物线
:
顶点是点
,且与
轴的正半轴交于点
.当
是直角三角形时,抛物线
的解析式为
.
【答案】
或
【解析】由
和
知:,,
.
抛物线
的顶点
在
轴上,
抛物线
的解析式为
.
设点
坐标为
,
,,
是直角三角形,
则:①当
时,,
即
,解得:,
,
将点
坐标代入
得:,解得:,
抛物线
的解析式为:,
②当
时,,
即
,解得:,
,
将点
坐标代入
得:,解得:,
抛物线
的解析式为:,
综上,当
为直角三角形时,抛物线
的解析式为
或
.
故答案是:
或
.
【知识点】二次函数与三角形综合、二次函数的解析式
(2019·杭州市拱墅区·期末)已知点
,,
都在直线
上,点
是线段
的中点,设
,,则线段
的长为
.(用含
,
的代数式表示)
【答案】
,,
【解析】根据题意可知:,,
所在的位置如图所示.
①当
在
左边时,如图所示:
,,
,
又
是
的中点,
②当
在
之间时,如图所示:
③当
在
之间时,如图所示:
,
④当
在
右边时,如图所示:
,
综上所述,
的长可为:,,.
【知识点】线段的和差
三、解答题
(2018·广州市白云区·期末)在平面内有四点,,,,,如图,请用直尺和圆规作图完成.(不写作法,保留画图痕迹).
()画直线
.
()画射线
与直线
交于
.
()连接
并延长
到
,使
.
()在线段
上找的一点
,使
的值最小.
【答案】()如图所示,直线
即为所求;
()如图所示,射线
即为所求;
()如图所示,线段
即为所求;
()如图所示,点
即为所求.
【知识点】两点之间线段最短、线段的画法、直线、射线、线段的画法
(2020·上海·专项)钟面上从
点到
点有几次时针与分针夹成
的角?分别是几点几分?
【答案】共有
次时针与分针所夹的角为
,
根据时针与分针的速度可知分针比时针每分钟转动快
,
第
次正好为
点整;
第
次设为
点
分时,时针与分针的夹角为
,
则
,解得
;
第
次设为
点
分时,时针与分针的夹角为
,
则
,解得
;
第
次设为
点
分时,时针与分针的夹角为
,
则
,解得
.
综上,钟面上从
点到
点有
次时针与分针夹成
角,
分别是
点整,
点
分,
点
分,
点
分.
【知识点】钟面角
(2020·单元测试)如图(),在长方形纸片
中,点
在边
上,点
,
分别在边
,
上,分别以
,
为折痕进行折叠并压平,点
,
的对应点分别是点
和点
.
【知识点】角的计算、轴对称的性质
(1)
如图(),若点
落在
上,求
的度数;
【答案】由翻折,知
和
重合,
和
重合,
所以
,.
因为
,
所以
(2)
如图(),若
,求
的度数;
【答案】由(),知
,,
因为
,
所以
.
所以
.
所以
.
(3)
如图(),若
,请直接写出
的度数;
【答案】
.
【解析】因为
,
所以
.
所以
.
则
(4)
若
,直接写出
的度数(用含
的代数式表示).
【答案】
或
.
【解析】如题图(),
因为
,
所以
.
因为
,,
所以
.
所以
如题图(),
因为
,,
所以
.
因为
,,
所以
.
所以
综上所述,
的度数为
或
.
一、选择题
(2019·上海松江区·期末)如图,四条表示方向的射线,表示北偏东
的是
A.
B.
C.
D.
(2019·广州市黄埔区·模拟)如图,在正方形
中,,
是对角线
上的两个动点,
是正方形四边上的任意一点,且
,,设
,在下列关于
是等腰三角形和对应
点个数的说法中,
①当
(即
,
两点重合)时,
点有
个;
②当
点有
个时,;
③当
是等边三角形时,
点有
个;
④当
时,
点最多有
个.
其中结论正确的是
A.①②
B.①③
C.②③
D.③④
(2019·宁波市镇海区)在直线
上且到
轴或
轴距离为
的点有
A.
个
B.
个
C.
个
D.
个
(2019·石家庄市桥西区)点
,,
在同一直线上,已知
,,则线段
的长是
A.
B.
C.
D.
或
(2019·深圳市龙岗区)已知
,,
都是非零有理数,满足
,令
,则
的值为
A.
B.
C.
D.
(2019·杭州市余杭区·模拟)蜂巢的构造非常美丽、科学,如图是由
个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,
的顶点都在格点上.设定
边如图所示,则
是直角三角形的个数有
A.
个
B.
个
C.
个
D.
个
(2019·东莞市莞城区·模拟)如图,在平行四边形
中,,,,点
从点
出发沿着
的路径运动,同时点
从点
出发沿着
的路径以相同的速度运动,当点
到达点
时,点
随之停止运动,设点
运动的路程为
,,下列图象中大致反映
与
之间的函数关系的是
A.
B.
C.
D.
(2019·天津南开区·期末)
中,
厘米,,
厘米,点
为
的中点.如果点
在线段
上以
厘米/秒的速度由
点向
点运动,同时,点
在线段
上由
点向
点运动.若点
的运动速度为
厘米/秒,则当
与
全等时,
的值为
A.
B.
C.
或
D.
或
(2019·淮安市淮阴区·期末)点
在线段
上,下列条件中不能确定点
是线段
中点的是
A.
B.
C.
D.
(2019·哈尔滨市香坊区·期末)下列说法中,正确的有
个.
①如果
,那么
,;
②用圆规画圆时,若圆规两脚间的距离是
,则所画圆的半径为
;
③小红身高
米,老师身高
厘米,小红和老师身高的比是
;
④用四个圆心角都是
的扇形,一定可以拼成一个圆;
⑤圆锥体积等于圆柱体积的
.
A.
B.
C.
D.
(2018·拉萨市城关区·期末)设
是自然数,则
的值为
A.
或
B.
C.
D.
或
(2019·长春市朝阳区)已知等腰三角形的两边长
,
满足方程组
则此等腰三角形的周长为
A.
B.
C.
D.
或
(2019·济南市章丘区·期末)如图,
是直线
上一点,
平分
,,若
,则
为
A.
B.
C.
D.
二、填空题
(2019·海口市琼山区·期末)已知线段
和
在同一直线上,如果
,,则线段
和
的中点之间的距离为
.
(2018·无锡市梁溪区·期末)已知
,以
为顶点作射线
,若
,则
.
(2019·滨州市滨城区·期末)已知点
,点
,点
在同一条直线上,,,
为
的中点,则
,
.
(2020·上海·期末)时针从钟面上
点旋转到
点,共旋转了
.
(2018·无锡市滨湖区·期末)记抛物线
:
的顶点为
,抛物线
:
顶点是点
,且与
轴的正半轴交于点
.当
是直角三角形时,抛物线
的解析式为
.
(2019·杭州市拱墅区·期末)已知点
,,
都在直线
上,点
是线段
的中点,设
,,则线段
的长为
.(用含
,
的代数式表示)
三、解答题
(2018·广州市白云区·期末)在平面内有四点,,,,,如图,请用直尺和圆规作图完成.(不写作法,保留画图痕迹).
()画直线
.
()画射线
与直线
交于
.
()连接
并延长
到
,使
.
()在线段
上找的一点
,使
的值最小.
(2020·上海·专项)钟面上从
点到
点有几次时针与分针夹成
的角?分别是几点几分?
(2020·单元测试)如图(),在长方形纸片
中,点
在边
上,点
,
分别在边
,
上,分别以
,
为折痕进行折叠并压平,点
,
的对应点分别是点
和点
.
(1)
如图(),若点
落在
上,求
的度数;
(2)
如图(),若
,求
的度数;
(3)
如图(),若
,请直接写出
的度数;
(4)
若
,直接写出
的度数(用含
的代数式表示).
第四章基本平面图形
一、选择题
(2019·上海松江区·期末)如图,四条表示方向的射线,表示北偏东
的是
A.
B.
C.
D.
【答案】B
【知识点】方向角
(2019·广州市黄埔区·模拟)如图,在正方形
中,,
是对角线
上的两个动点,
是正方形四边上的任意一点,且
,,设
,在下列关于
是等腰三角形和对应
点个数的说法中,
①当
(即
,
两点重合)时,
点有
个;
②当
点有
个时,;
③当
是等边三角形时,
点有
个;
④当
时,
点最多有
个.
其中结论正确的是
A.①②
B.①③
C.②③
D.③④
【答案】B
【解析】①如图,当
(即
,
两点重合)时,
点有
个,故正确;
②当
点有
个时,当
或
或
或
时,
点有
个,故错误;
③如图,当
是等边三角形时,
点有
个,故正确;
④当
时,
点最多有
个,故错误.
【知识点】正方形的性质、圆周角定理推论、等腰三角形的性质
(2019·宁波市镇海区)在直线
上且到
轴或
轴距离为
的点有
A.
个
B.
个
C.
个
D.
个
【答案】C
【解析】距离
轴距离为
的点,定在直线
或
上,
令
得
,
为
,
令
得
,
为
,
距离
轴距离为
的点,定在直线
或
上,
令
,得
,
为
,
令
,得
,
为
,
有重合两点,
共有
,,
三点.
【知识点】一次函数图像上点的坐标特征
(2019·石家庄市桥西区)点
,,
在同一直线上,已知
,,则线段
的长是
A.
B.
C.
D.
或
【答案】D
【解析】当点
在线段
上时,
,,
,
当点
在线段
的延长线上时,
,,
.
【知识点】线段的和差
(2019·深圳市龙岗区)已知
,,
都是非零有理数,满足
,令
,则
的值为
A.
B.
C.
D.
【答案】B
【解析】①当
,,
为两正一负时:,
,则
;
②当
,,
为两负一正时:,,
则
;
由①②知则
的所有可能的值为
.
故选B.
【知识点】简单的代数式求值
(2019·杭州市余杭区·模拟)蜂巢的构造非常美丽、科学,如图是由
个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,
的顶点都在格点上.设定
边如图所示,则
是直角三角形的个数有
A.
个
B.
个
C.
个
D.
个
【答案】D
【解析】如图,
是直角边时,点
共有
个位置,即有
个直角三角形;
是斜边时,点
共有
个位置,即有
个直角三角形,
综上所述,
是直角三角形的个数有
个.
【知识点】直角三角形的性质与判定、多边形的相关概念
(2019·东莞市莞城区·模拟)如图,在平行四边形
中,,,,点
从点
出发沿着
的路径运动,同时点
从点
出发沿着
的路径以相同的速度运动,当点
到达点
时,点
随之停止运动,设点
运动的路程为
,,下列图象中大致反映
与
之间的函数关系的是
A.
B.
C.
D.
【答案】B
【解析】在
中,,,,
.
当
时,,,
;
当
时,,,
;
当
时,,,
.
【知识点】分段函数、y=ax^2+bx+c的图象
(2019·天津南开区·期末)
中,
厘米,,
厘米,点
为
的中点.如果点
在线段
上以
厘米/秒的速度由
点向
点运动,同时,点
在线段
上由
点向
点运动.若点
的运动速度为
厘米/秒,则当
与
全等时,
的值为
A.
B.
C.
或
D.
或
【答案】D
【解析】当
时,
与
全等,
点
为
的中点,
,
,
,
点
在线段
上以
厘米/秒的速度由
点向
点运动,
运动时间时
,
,
,
;
当
时,,
,,
,
,
,
运动时间为
,
.
故
的值为
或
.
【知识点】边角边
(2019·淮安市淮阴区·期末)点
在线段
上,下列条件中不能确定点
是线段
中点的是
A.
B.
C.
D.
【答案】B
【解析】A、
,则点
是线段
中点;
B、
,则
可以是线段
上任意一点;
C、
,则点
是线段
中点;
D、
,则点
是线段
中点.
【知识点】线段的和差
(2019·哈尔滨市香坊区·期末)下列说法中,正确的有
个.
①如果
,那么
,;
②用圆规画圆时,若圆规两脚间的距离是
,则所画圆的半径为
;
③小红身高
米,老师身高
厘米,小红和老师身高的比是
;
④用四个圆心角都是
的扇形,一定可以拼成一个圆;
⑤圆锥体积等于圆柱体积的
.
A.
B.
C.
D.
【答案】B
【解析】①如果
,那么
,
或
,
等,本说法错误;
②用圆规画圆时,若圆规两脚间的距离是
,则所画圆的半径为
,本说法正确;
③小红身高
米,即
厘米,老师身高
厘米,
小红和老师身高的比是
,即
,本说法正确;
④用四个圆心角都是
、半径相等的扇形,一定可以拼成一个圆,当半径不相等时,不能拼成一个圆,本说法错误;
⑤底面积相等、高相等时,圆锥体积等于圆柱体积的
,如果不确定底面积相等、高相等,圆锥体积不一定等于圆柱体积的
,本说法错误.
【知识点】圆的定义
(2018·拉萨市城关区·期末)设
是自然数,则
的值为
A.
或
B.
C.
D.
或
【答案】A
【解析】因为
为自然数,且
与
是两个整数,所以
与
必定同是偶数,或同是奇数;
又因为
的奇数次幂是
,
的偶数次幂是
,
所以,若
和
同为偶数,则
;若
和
同为奇数,则
.
【知识点】有理数的乘方
(2019·长春市朝阳区)已知等腰三角形的两边长
,
满足方程组
则此等腰三角形的周长为
A.
B.
C.
D.
或
【答案】A
【解析】
解不等式组可得
等腰三角形的两边长为
,,
三边可能情况为
,,
或
,,,
,,
不能构成三角形,
等腰三角形的周长为
.
【知识点】等腰三角形的概念
(2019·济南市章丘区·期末)如图,
是直线
上一点,
平分
,,若
,则
为
A.
B.
C.
D.
【答案】B
【解析】
,
,
平分
,
,
,
.
【知识点】角的计算、角平分线的定义
二、填空题
(2019·海口市琼山区·期末)已知线段
和
在同一直线上,如果
,,则线段
和
的中点之间的距离为
.
【答案】
或
【解析】此题有两种情况:
①当
点在线段
上,此时
,
而
,.
,
线段
和
的中点之间的距离为:
;
②当
点在线段
上,此时
,
而
,.
,
线段
和
的中点之间的距离为:
.
【知识点】线段的和差、线段中点的概念及计算
(2018·无锡市梁溪区·期末)已知
,以
为顶点作射线
,若
,则
.
【答案】
或
【解析】
,,
,
当
在
下方时,;
当
在
上方时,.
故答案为:
或
.
【知识点】角的计算
(2019·滨州市滨城区·期末)已知点
,点
,点
在同一条直线上,,,
为
的中点,则
,
.
【答案】
或
;
或
【知识点】线段中点的概念及计算、线段的和差
(2020·上海·期末)时针从钟面上
点旋转到
点,共旋转了
.
【答案】
【知识点】钟面角
(2018·无锡市滨湖区·期末)记抛物线
:
的顶点为
,抛物线
:
顶点是点
,且与
轴的正半轴交于点
.当
是直角三角形时,抛物线
的解析式为
.
【答案】
或
【解析】由
和
知:,,
.
抛物线
的顶点
在
轴上,
抛物线
的解析式为
.
设点
坐标为
,
,,
是直角三角形,
则:①当
时,,
即
,解得:,
,
将点
坐标代入
得:,解得:,
抛物线
的解析式为:,
②当
时,,
即
,解得:,
,
将点
坐标代入
得:,解得:,
抛物线
的解析式为:,
综上,当
为直角三角形时,抛物线
的解析式为
或
.
故答案是:
或
.
【知识点】二次函数与三角形综合、二次函数的解析式
(2019·杭州市拱墅区·期末)已知点
,,
都在直线
上,点
是线段
的中点,设
,,则线段
的长为
.(用含
,
的代数式表示)
【答案】
,,
【解析】根据题意可知:,,
所在的位置如图所示.
①当
在
左边时,如图所示:
,,
,
又
是
的中点,
②当
在
之间时,如图所示:
③当
在
之间时,如图所示:
,
④当
在
右边时,如图所示:
,
综上所述,
的长可为:,,.
【知识点】线段的和差
三、解答题
(2018·广州市白云区·期末)在平面内有四点,,,,,如图,请用直尺和圆规作图完成.(不写作法,保留画图痕迹).
()画直线
.
()画射线
与直线
交于
.
()连接
并延长
到
,使
.
()在线段
上找的一点
,使
的值最小.
【答案】()如图所示,直线
即为所求;
()如图所示,射线
即为所求;
()如图所示,线段
即为所求;
()如图所示,点
即为所求.
【知识点】两点之间线段最短、线段的画法、直线、射线、线段的画法
(2020·上海·专项)钟面上从
点到
点有几次时针与分针夹成
的角?分别是几点几分?
【答案】共有
次时针与分针所夹的角为
,
根据时针与分针的速度可知分针比时针每分钟转动快
,
第
次正好为
点整;
第
次设为
点
分时,时针与分针的夹角为
,
则
,解得
;
第
次设为
点
分时,时针与分针的夹角为
,
则
,解得
;
第
次设为
点
分时,时针与分针的夹角为
,
则
,解得
.
综上,钟面上从
点到
点有
次时针与分针夹成
角,
分别是
点整,
点
分,
点
分,
点
分.
【知识点】钟面角
(2020·单元测试)如图(),在长方形纸片
中,点
在边
上,点
,
分别在边
,
上,分别以
,
为折痕进行折叠并压平,点
,
的对应点分别是点
和点
.
【知识点】角的计算、轴对称的性质
(1)
如图(),若点
落在
上,求
的度数;
【答案】由翻折,知
和
重合,
和
重合,
所以
,.
因为
,
所以
(2)
如图(),若
,求
的度数;
【答案】由(),知
,,
因为
,
所以
.
所以
.
所以
.
(3)
如图(),若
,请直接写出
的度数;
【答案】
.
【解析】因为
,
所以
.
所以
.
则
(4)
若
,直接写出
的度数(用含
的代数式表示).
【答案】
或
.
【解析】如题图(),
因为
,
所以
.
因为
,,
所以
.
所以
如题图(),
因为
,,
所以
.
因为
,,
所以
.
所以
综上所述,
的度数为
或
.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
