北师大版七年级数学上册单元练习第二章有理数及其运算(word版含解析)
文档属性
| 名称 | 北师大版七年级数学上册单元练习第二章有理数及其运算(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 649.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 07:40:34 | ||
图片预览




文档简介
第二章有理数及其运算
一、选择题
(2019·无锡市锡山区·期末)如图,在
中,,,,点
是
上的一点,点
是
上的一点,,当
与
中的一个角相等时,则
的值为
A.
或
B.
或
C.
或
D.
或
(2019·天津和平区·模拟)如图,在菱形
中,,,点
是这个菱形内部或边上的一点,若以点
,,
为顶点的三角形是等腰三角形,则
,(,
两点不重合)两点间的最短距离为多少?
A.
B.
C.
D.
(2020·湖南湘西土家族苗族自治州·真题)
年中国与“一带一路”沿线国家货物贸易进出口总额达到
亿元,用科学记数法表示
是
A.
B.
C.
D.
(2018·苏州市高新区·模拟)如图,已知
,
是反比例函数
图象上的两点,,交
轴于点
,动点
从坐标原点
出发,沿
匀速运动,终点为
,过点
作
,,垂足分别为
,.设四边形
的面积为
,点
运动的时间为
,则
关于
的函数图象大致为
A.
B.
C.
D.
(2018·甘肃兰州市·期末)已知
是关于
的方程
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的两条边长,则
的周长为
A.
B.
C.
D.
或
(2018·沈阳市沈北新区)
,则下面结论中正确的是
A.
没有最小值
B.只有一个
使
有最小值
C.有限个
使
取得最小值
D.有无数多个
使
取得最小值
(2019·杭州市上城区·模拟)若关于
的不等式
的解都能使不等式
成立,则
的取值范围是
A.
或
B.
C.
D.
(2019·杭州市萧山区)如图,
为
直径
上一动点,过点
的直线交
于
,
两点,且
,
于点
,
于点
,当点
在
上运动时.设
,,下列中图象中,能表示
与
的函数关系式的图象大致是
A.
B.
C.
D.
(2018·石家庄市高邑县·期末)如图,在
中,已知
,,,动点
从点
出发,以
的速度沿线段
向点
运动,在运动过程中,当
为等腰三角形时,点
出发的时刻
可能的值为
A.
B.
或
C.
D.
或
(2020·天津红桥区·模拟)点
,
在数轴上的位置如图所示,其对应的实数分别是
,,下列结论正确的是
A.
B.
C.
D.
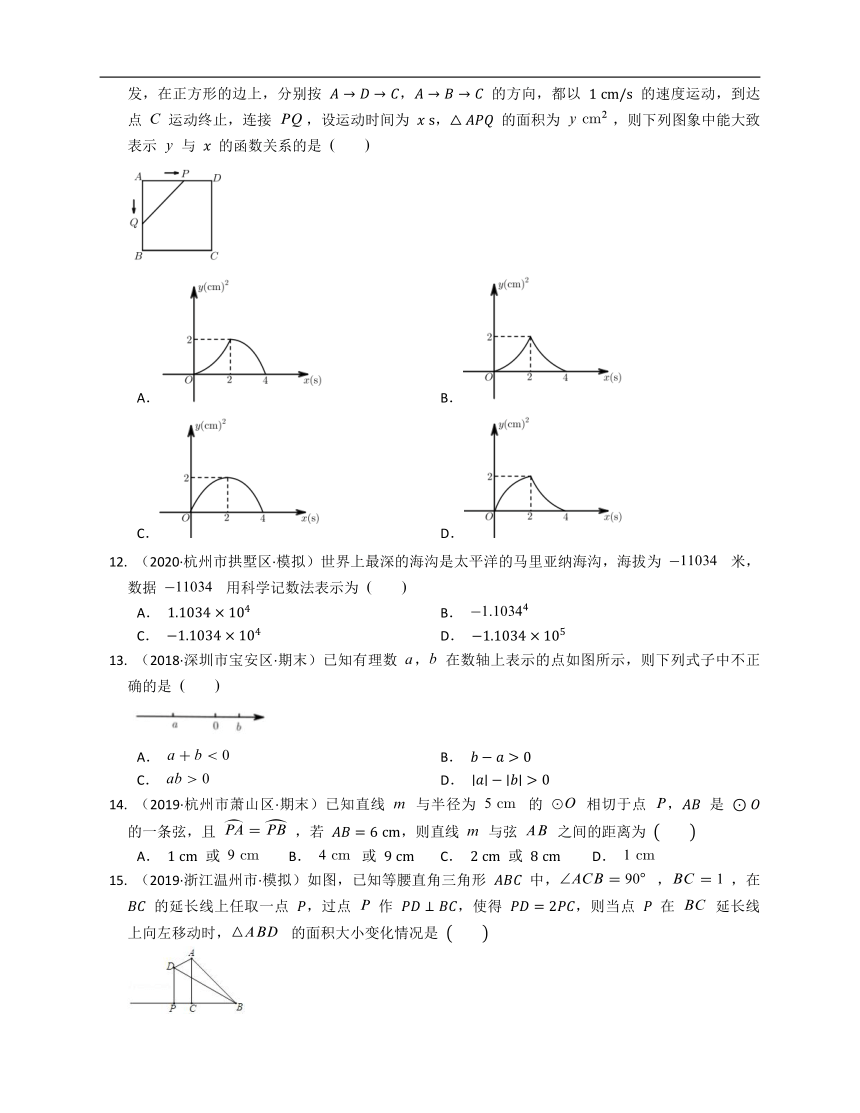
(2018·合肥市长丰县·期末)如图,正方形
的边长为
,动点
,
同时从点
出发,在正方形的边上,分别按
,
的方向,都以
的速度运动,到达点
运动终止,连接
,设运动时间为
,
的面积为
,则下列图象中能大致表示
与
的函数关系的是
A.
B.
C.
D.
(2020·杭州市拱墅区·模拟)世界上最深的海沟是太平洋的马里亚纳海沟,海拔为
米,数据
用科学记数法表示为
A.
B.
C.
D.
(2018·深圳市宝安区·期末)已知有理数
,
在数轴上表示的点如图所示,则下列式子中不正确的是
A.
B.
C.
D.
(2019·杭州市萧山区·期末)已知直线
与半径为
的
相切于点
,
是
的一条弦,且
,若
,则直线
与弦
之间的距离为
A.
或
B.
或
C.
或
D.
(2019·浙江温州市·模拟)如图,已知等腰直角三角形
中,,,在
的延长线上任取一点
,过点
作
,使得
,则当点
在
延长线上向左移动时,
的面积大小变化情况是
A.一直变大
B.一直变小
C.先变小再变大
D.先变大再变小
(2018·苏州市常熟市)直角三角形的两边长为
和
,则此三角形的外接圆半径为
A.
B.
C.
或
D.
或
(2019·洛阳市汝阳县)已知四个数:,,,,任取其中两个数相乘,所得积的最大值是
A.
B.
C.
D.
(2021·专项)如图①,点
是
的中点,点
在
上,动点
以每秒
的速度沿图①()的边线运动,运动路径为:,相应的
的面积
关于运动时间
的函数图象如图②,若
,有下列结论:
①图①中的
长是
;
②图②中的
点表示第
秒时,
的值为
;
③图②中的
点表示第
秒时,
的值为
.
其中,正确结论的个数是
A.
B.
C.
D.
(2019·天津红桥区)已知
,,且
,则
的值为
A.
B.
C.
或
D.
或
二、填空题
(2019·南通市崇川区·期末)已知射线
,从
点再引射线
,,使
,,则
的度数为
.
(2019·济南市槐荫区·期末)已知
,,
位置如图,则化简
.
(2019·株洲市醴陵市·期末)定义:等腰三角形的顶角与其一个底角的度数的比值
称为这个等腰三角形的“特征值”.若等腰
中,,则它的特征值
.
(2020·苏州市太仓市·调研)如图,
中,,,,点
是
边上一点,,点
是线段
上的动点,连接
,以
为斜边在
的下方作等腰
,连接
,当
从点
出发运动至点
停止的过程中,
面积的最大值等于
.
(2020·单元测试)计算:
()
;
()
;
()
;
()
.
(2018·成都市锦江区)设一组数据:,,,,,我们将前
个数之和记作
,即
,,,,,定义
为这组数据的“嘉祥数”,若
,,,,
这十个数据的“嘉祥数”为
,则
,,,,,
这
个数据的“嘉祥数”为
.
(2020·单元测试)如图,圆的周长为
个单位长度.在该圆的
等分点处分别标上数字
,,,,先让圆周上表示数字
的点与数轴上表示数
的点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示数
的点与圆周上表示数字
的点重合.
(2020·单元测试)先运用乘法运算律将下列算式变形,再计算出结果.
()
;
()
;
()
;
()
.
(2019·洛阳市汝阳县)某景点
月
日的最低气温为
,最高气温为
,那么该景点这天的是温差是
.
三、解答题
(2018·保定市定州市)计算:
(1)
;
(2)
;
(3)
.
(2019·济南市天桥区)按要求作答.
(1)
【问题发现】
如图
,在
中,,,点
为
的中点,以
为一边作正方形
,点
恰好与点
重合,则线段
与
的数量关系为
.
(2)
【拓展研究】
在()的条件下,如果正方形
绕点
旋转,连接
,,,线段
与
的数量关系有无变化?请仅就图
的情形给出证明.
(3)
【问题发现】
当正方形
旋转到
,,
三点共线的时候,直接写出线段
的长.
(2020·江苏徐州市)如图,已知点
,,.
(1)
将
绕点
逆时针旋转
得
,画出
,并写出点
的对应点
的坐标为
;
(2)
画出
关于原点成中心对称的图形
,并写出点
的对应点
的坐标为
;
.
(3)
在平面直角坐标系内找点
,使得
,,,
为顶点的四边形为平行四边形,则点
的坐标为
.
(2019·烟台市招远市)明明同学计算
时,他是这样做的:
(1)
明明的解法从第几步开始出现错误,改正后并计算出正确的结果:
(2)
仿照明明的解法,请你计算:.
(2019·广州市越秀区·期末)计算:
(1)
.
(2)
.
第二章有理数及其运算
一、选择题
(2019·无锡市锡山区·期末)如图,在
中,,,,点
是
上的一点,点
是
上的一点,,当
与
中的一个角相等时,则
的值为
A.
或
B.
或
C.
或
D.
或
【答案】D
【解析】
,
,设
,,
①当
时,可得
,
,
,
,
;
②当
时,
如图中,过点
作
,可得
,
,
,
,,
,
,,
,
,
,
,
.
综上所述,.
【知识点】两角分别相等
(2019·天津和平区·模拟)如图,在菱形
中,,,点
是这个菱形内部或边上的一点,若以点
,,
为顶点的三角形是等腰三角形,则
,(,
两点不重合)两点间的最短距离为多少?
A.
B.
C.
D.
【答案】D
【解析】在菱形
中,
,,
,
都是等边三角形.
①若以边
为底,则
垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“,即当点
与点
重合时,
值最小,最小值为
;
②若以边
为底,
为顶角时,以点
为圆心,
长为半径作圆,与
相交于一点,则弧
(除点
外)上的所有点都满足
是等腰三角形,当点
在
上时,
最小,最小值为
;
③若以边
为底,
为顶角,以点
为圆心,
为半径作圆,则弧
上的点
与点
均满足
为等腰三角形,当点
与点
重合时,
最小,显然不满足题意,故此种情况不存在.
综上所述,
的最小值为
.
【知识点】菱形的性质
(2020·湖南湘西土家族苗族自治州·真题)
年中国与“一带一路”沿线国家货物贸易进出口总额达到
亿元,用科学记数法表示
是
A.
B.
C.
D.
【答案】B
【解析】
.
【知识点】正指数科学记数法
(2018·苏州市高新区·模拟)如图,已知
,
是反比例函数
图象上的两点,,交
轴于点
,动点
从坐标原点
出发,沿
匀速运动,终点为
,过点
作
,,垂足分别为
,.设四边形
的面积为
,点
运动的时间为
,则
关于
的函数图象大致为
A.
B.
C.
D.
【答案】A
【解析】①点
在
上运动时,此时四边形
的面积
,保持不变,故排除B、D;
②点
在
上运动时,设路线
的总路程为
,点
的速度为
,则
,
因为
,,
均是常数,
所以
与
成一次函数关系.故排除C.
【知识点】反比例函数系数k的几何意义
(2018·甘肃兰州市·期末)已知
是关于
的方程
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的两条边长,则
的周长为
A.
B.
C.
D.
或
【答案】C
【解析】把
代入方程
得
,解得
,
方程化为
,解得
,,
,不能构造三角形,
三角形三边为
,,,
的周长为
.
【知识点】一元二次方程的根
(2018·沈阳市沈北新区)
,则下面结论中正确的是
A.
没有最小值
B.只有一个
使
有最小值
C.有限个
使
取得最小值
D.有无数多个
使
取得最小值
【答案】D
【解析】
表示数轴上一点
到
,
的距离和,这个距离和的最小值为
,此时
的范围为
,故选:D.
【知识点】绝对值的几何意义
(2019·杭州市上城区·模拟)若关于
的不等式
的解都能使不等式
成立,则
的取值范围是
A.
或
B.
C.
D.
【答案】C
【解析】
关于
的不等式
的解都能使不等式
成立,
,即
,
解不等式
,得:,
则有:,
解得:,
则
的取值范围是
.
故选:C.
【知识点】含参一元一次方程的解法、不等式的性质
(2019·杭州市萧山区)如图,
为
直径
上一动点,过点
的直线交
于
,
两点,且
,
于点
,
于点
,当点
在
上运动时.设
,,下列中图象中,能表示
与
的函数关系式的图象大致是
A.
B.
C.
D.
【答案】A
【解析】点
从点
运动到点
的过程中,
的值逐渐增大,
的长度随
值的变化先变大再变小,当
与
重合时,
有最大值,
,,
时,
过点
,
此时:,,,
所以,随着
的增大,
先增后降,类抛物线.
【知识点】图像法
(2018·石家庄市高邑县·期末)如图,在
中,已知
,,,动点
从点
出发,以
的速度沿线段
向点
运动,在运动过程中,当
为等腰三角形时,点
出发的时刻
可能的值为
A.
B.
或
C.
D.
或
【答案】D
【知识点】等腰三角形的概念
(2020·天津红桥区·模拟)点
,
在数轴上的位置如图所示,其对应的实数分别是
,,下列结论正确的是
A.
B.
C.
D.
【答案】D
【解析】由数轴的定义得:,.
,,则选项A,B均错误;
,
.
,则选项C错误;
,,
,,即
,则选项D正确.
【知识点】绝对值的几何意义
(2018·合肥市长丰县·期末)如图,正方形
的边长为
,动点
,
同时从点
出发,在正方形的边上,分别按
,
的方向,都以
的速度运动,到达点
运动终止,连接
,设运动时间为
,
的面积为
,则下列图象中能大致表示
与
的函数关系的是
A.
B.
C.
D.
【答案】A
【解析】①当
时,
正方形的边长为
,
;
②当
时,
与
之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A选项图象符合.
【知识点】y=ax^2+bx+c的图象
(2020·杭州市拱墅区·模拟)世界上最深的海沟是太平洋的马里亚纳海沟,海拔为
米,数据
用科学记数法表示为
A.
B.
C.
D.
【答案】C
【解析】将
用科学记数法表示为:.
【知识点】正指数科学记数法
(2018·深圳市宝安区·期末)已知有理数
,
在数轴上表示的点如图所示,则下列式子中不正确的是
A.
B.
C.
D.
【答案】C
【解析】
在数轴上的位置可知,,,
A、
,,
,故A选项正确;
B、
,
,故B选项正确;
C、
,
,故C选项错误;
D、
,,
,故D选项正确.
故选C.
【知识点】有理数的乘法
(2019·杭州市萧山区·期末)已知直线
与半径为
的
相切于点
,
是
的一条弦,且
,若
,则直线
与弦
之间的距离为
A.
或
B.
或
C.
或
D.
【答案】A
【解析】连接
,
交
与
.
,
,,
直线
是切线,
,
,
在
中,,
,
同法当弦
在点
下方时,.
【知识点】切线的性质
(2019·浙江温州市·模拟)如图,已知等腰直角三角形
中,,,在
的延长线上任取一点
,过点
作
,使得
,则当点
在
延长线上向左移动时,
的面积大小变化情况是
A.一直变大
B.一直变小
C.先变小再变大
D.先变大再变小
【答案】C
【解析】当
与
的交点在线段
上时,如图
所示.
设
,则
,,则
的面积随
的增大而减小;
当
与
的交点在线段
的延长线上时,如图
所示.
设
,则
,,
,
,即
,
,
,
的面积是:,
的面积随
的增大而增大,
由上可得,
的面积随
的增大先变小后变大.
【知识点】基本定理、k,b对一次函数图象及性质的影响
(2018·苏州市常熟市)直角三角形的两边长为
和
,则此三角形的外接圆半径为
A.
B.
C.
或
D.
或
【答案】D
【解析】由勾股定理可知:
①当
为斜边时,直角三角形的斜边长为:;
②当
为直角边时,直角三角形的斜边长为:;
因此这个三角形的外接圆半径为
或
.
【知识点】三角形的外接圆与外心
(2019·洛阳市汝阳县)已知四个数:,,,,任取其中两个数相乘,所得积的最大值是
A.
B.
C.
D.
【答案】B
【解析】依题意得两个数相乘所得积的最大值是
.
故选B.
【知识点】有理数的乘法
(2021·专项)如图①,点
是
的中点,点
在
上,动点
以每秒
的速度沿图①()的边线运动,运动路径为:,相应的
的面积
关于运动时间
的函数图象如图②,若
,有下列结论:
①图①中的
长是
;
②图②中的
点表示第
秒时,
的值为
;
③图②中的
点表示第
秒时,
的值为
.
其中,正确结论的个数是
A.
B.
C.
D.
【答案】D
【知识点】行程问题
(2019·天津红桥区)已知
,,且
,则
的值为
A.
B.
C.
或
D.
或
【答案】D
【解析】
,
,
,
,
又
,由于
,,而
,,
则
只能取
,
取
或
,
或
.
则
的值为
或
.
【知识点】绝对值的性质
二、填空题
(2019·南通市崇川区·期末)已知射线
,从
点再引射线
,,使
,,则
的度数为
.
【答案】
或
【解析】如图所示.
①
在
,
之间,
,,
②
在
,
之间,
,,
【知识点】角的计算
(2019·济南市槐荫区·期末)已知
,,
位置如图,则化简
.
【答案】
【解析】
由图可知
,,,
,,,
.
【知识点】绝对值的化简、绝对值的几何意义
(2019·株洲市醴陵市·期末)定义:等腰三角形的顶角与其一个底角的度数的比值
称为这个等腰三角形的“特征值”.若等腰
中,,则它的特征值
.
【答案】
或
【解析】①当
为顶角时,等腰三角形两底角的度数为:,
特征值
.
②当
为底角时,顶角的度数为:,
特征值
.
综上所述,特征值
为
或
.
【知识点】等边对等角
(2020·苏州市太仓市·调研)如图,
中,,,,点
是
边上一点,,点
是线段
上的动点,连接
,以
为斜边在
的下方作等腰
,连接
,当
从点
出发运动至点
停止的过程中,
面积的最大值等于
.
【答案】
【解析】设
,
①如图
,当
时,作
于
,
于
,
,
四边形
中,,,
,
,
,
在
和
,
,,,
,
,
,
四边形
是正方形,
设
,则
,得
,即有
,
,,
,
当
时,.
②如图
,
当
时,同理可得
,
当
时,.
综上,当
时,.
【知识点】正方形的概念、二次函数的最值
(2020·单元测试)计算:
()
;
()
;
()
;
()
.
【答案】
;
;
;
【知识点】有理数的加减乘除乘方混合运算
(2018·成都市锦江区)设一组数据:,,,,,我们将前
个数之和记作
,即
,,,,,定义
为这组数据的“嘉祥数”,若
,,,,
这十个数据的“嘉祥数”为
,则
,,,,,
这
个数据的“嘉祥数”为
.
【答案】
【解析】
,
则
嘉祥数为
.
【知识点】有理数的加法法则及计算
(2020·单元测试)如图,圆的周长为
个单位长度.在该圆的
等分点处分别标上数字
,,,,先让圆周上表示数字
的点与数轴上表示数
的点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示数
的点与圆周上表示数字
的点重合.
【答案】
【知识点】数轴的概念
(2020·单元测试)先运用乘法运算律将下列算式变形,再计算出结果.
()
;
()
;
()
;
()
.
【答案】
;
;
;
;
;
;
;
【知识点】有理数的乘法
(2019·洛阳市汝阳县)某景点
月
日的最低气温为
,最高气温为
,那么该景点这天的是温差是
.
【答案】
【解析】
.
【知识点】有理数减法的应用
三、解答题
(2018·保定市定州市)计算:
【知识点】有理数的加减乘除乘方混合运算、有理数加减乘除混合运算
(1)
;
【答案】
(2)
;
【答案】
(3)
.
【答案】
(2019·济南市天桥区)按要求作答.
【知识点】两角分别相等、正方形的性质
(1)
【问题发现】
如图
,在
中,,,点
为
的中点,以
为一边作正方形
,点
恰好与点
重合,则线段
与
的数量关系为
.
【答案】
【解析】在
中,,
根据勾股定理得,,
点
为
的中点,
,
四边形
是正方形,
,
,
.
(2)
【拓展研究】
在()的条件下,如果正方形
绕点
旋转,连接
,,,线段
与
的数量关系有无变化?请仅就图
的情形给出证明.
【答案】无变化;
如图
,在
中,,
,
,
在正方形
中,,
在
中,,
,
,
,
,
,
,
,
线段
与
的数量关系无变化.
(3)
【问题发现】
当正方形
旋转到
,,
三点共线的时候,直接写出线段
的长.
【答案】
或
【解析】当点
在线段
上时,如图
,
由()知,,
在
中,,,
根据勾股定理得,,
,
由()知,,
,
当点
在线段
的延长线上时,如图
,
在
中,,
,
,
在正方形
中,,
在
中,,
,
,
,
,
,
,
,
由()知,,
在
中,,,
根据勾股定理得,,
,
由()知,,
.
即:当正方形
旋转到
,,
三点共线时候,线段
的长为
或
.
(2020·江苏徐州市)如图,已知点
,,.
【知识点】坐标平面内图形的旋转变换、平行四边形及其性质
(1)
将
绕点
逆时针旋转
得
,画出
,并写出点
的对应点
的坐标为
;
【答案】如图,
即为所求.
【解析】点
的坐标为
.
故答案为
.
(2)
画出
关于原点成中心对称的图形
,并写出点
的对应点
的坐标为
;
【答案】
即为所求.
【解析】点
的坐标为
.
故答案为
.
(3)
在平面直角坐标系内找点
,使得
,,,
为顶点的四边形为平行四边形,则点
的坐标为
.
【答案】
或
或
【解析】如图,满足条件的点
的坐标为
或
或
.
故答案为
或
或
.
(2019·烟台市招远市)明明同学计算
时,他是这样做的:
【知识点】有理数加减混合运算
(1)
明明的解法从第几步开始出现错误,改正后并计算出正确的结果:
【答案】明明的解法从第三步开始出现错误,
改正:
(2)
仿照明明的解法,请你计算:.
【答案】
(2019·广州市越秀区·期末)计算:
【知识点】有理数的加减乘除乘方混合运算、有理数加减混合运算
(1)
.
【答案】
(2)
.
【答案】
一、选择题
(2019·无锡市锡山区·期末)如图,在
中,,,,点
是
上的一点,点
是
上的一点,,当
与
中的一个角相等时,则
的值为
A.
或
B.
或
C.
或
D.
或
(2019·天津和平区·模拟)如图,在菱形
中,,,点
是这个菱形内部或边上的一点,若以点
,,
为顶点的三角形是等腰三角形,则
,(,
两点不重合)两点间的最短距离为多少?
A.
B.
C.
D.
(2020·湖南湘西土家族苗族自治州·真题)
年中国与“一带一路”沿线国家货物贸易进出口总额达到
亿元,用科学记数法表示
是
A.
B.
C.
D.
(2018·苏州市高新区·模拟)如图,已知
,
是反比例函数
图象上的两点,,交
轴于点
,动点
从坐标原点
出发,沿
匀速运动,终点为
,过点
作
,,垂足分别为
,.设四边形
的面积为
,点
运动的时间为
,则
关于
的函数图象大致为
A.
B.
C.
D.
(2018·甘肃兰州市·期末)已知
是关于
的方程
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的两条边长,则
的周长为
A.
B.
C.
D.
或
(2018·沈阳市沈北新区)
,则下面结论中正确的是
A.
没有最小值
B.只有一个
使
有最小值
C.有限个
使
取得最小值
D.有无数多个
使
取得最小值
(2019·杭州市上城区·模拟)若关于
的不等式
的解都能使不等式
成立,则
的取值范围是
A.
或
B.
C.
D.
(2019·杭州市萧山区)如图,
为
直径
上一动点,过点
的直线交
于
,
两点,且
,
于点
,
于点
,当点
在
上运动时.设
,,下列中图象中,能表示
与
的函数关系式的图象大致是
A.
B.
C.
D.
(2018·石家庄市高邑县·期末)如图,在
中,已知
,,,动点
从点
出发,以
的速度沿线段
向点
运动,在运动过程中,当
为等腰三角形时,点
出发的时刻
可能的值为
A.
B.
或
C.
D.
或
(2020·天津红桥区·模拟)点
,
在数轴上的位置如图所示,其对应的实数分别是
,,下列结论正确的是
A.
B.
C.
D.
(2018·合肥市长丰县·期末)如图,正方形
的边长为
,动点
,
同时从点
出发,在正方形的边上,分别按
,
的方向,都以
的速度运动,到达点
运动终止,连接
,设运动时间为
,
的面积为
,则下列图象中能大致表示
与
的函数关系的是
A.
B.
C.
D.
(2020·杭州市拱墅区·模拟)世界上最深的海沟是太平洋的马里亚纳海沟,海拔为
米,数据
用科学记数法表示为
A.
B.
C.
D.
(2018·深圳市宝安区·期末)已知有理数
,
在数轴上表示的点如图所示,则下列式子中不正确的是
A.
B.
C.
D.
(2019·杭州市萧山区·期末)已知直线
与半径为
的
相切于点
,
是
的一条弦,且
,若
,则直线
与弦
之间的距离为
A.
或
B.
或
C.
或
D.
(2019·浙江温州市·模拟)如图,已知等腰直角三角形
中,,,在
的延长线上任取一点
,过点
作
,使得
,则当点
在
延长线上向左移动时,
的面积大小变化情况是
A.一直变大
B.一直变小
C.先变小再变大
D.先变大再变小
(2018·苏州市常熟市)直角三角形的两边长为
和
,则此三角形的外接圆半径为
A.
B.
C.
或
D.
或
(2019·洛阳市汝阳县)已知四个数:,,,,任取其中两个数相乘,所得积的最大值是
A.
B.
C.
D.
(2021·专项)如图①,点
是
的中点,点
在
上,动点
以每秒
的速度沿图①()的边线运动,运动路径为:,相应的
的面积
关于运动时间
的函数图象如图②,若
,有下列结论:
①图①中的
长是
;
②图②中的
点表示第
秒时,
的值为
;
③图②中的
点表示第
秒时,
的值为
.
其中,正确结论的个数是
A.
B.
C.
D.
(2019·天津红桥区)已知
,,且
,则
的值为
A.
B.
C.
或
D.
或
二、填空题
(2019·南通市崇川区·期末)已知射线
,从
点再引射线
,,使
,,则
的度数为
.
(2019·济南市槐荫区·期末)已知
,,
位置如图,则化简
.
(2019·株洲市醴陵市·期末)定义:等腰三角形的顶角与其一个底角的度数的比值
称为这个等腰三角形的“特征值”.若等腰
中,,则它的特征值
.
(2020·苏州市太仓市·调研)如图,
中,,,,点
是
边上一点,,点
是线段
上的动点,连接
,以
为斜边在
的下方作等腰
,连接
,当
从点
出发运动至点
停止的过程中,
面积的最大值等于
.
(2020·单元测试)计算:
()
;
()
;
()
;
()
.
(2018·成都市锦江区)设一组数据:,,,,,我们将前
个数之和记作
,即
,,,,,定义
为这组数据的“嘉祥数”,若
,,,,
这十个数据的“嘉祥数”为
,则
,,,,,
这
个数据的“嘉祥数”为
.
(2020·单元测试)如图,圆的周长为
个单位长度.在该圆的
等分点处分别标上数字
,,,,先让圆周上表示数字
的点与数轴上表示数
的点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示数
的点与圆周上表示数字
的点重合.
(2020·单元测试)先运用乘法运算律将下列算式变形,再计算出结果.
()
;
()
;
()
;
()
.
(2019·洛阳市汝阳县)某景点
月
日的最低气温为
,最高气温为
,那么该景点这天的是温差是
.
三、解答题
(2018·保定市定州市)计算:
(1)
;
(2)
;
(3)
.
(2019·济南市天桥区)按要求作答.
(1)
【问题发现】
如图
,在
中,,,点
为
的中点,以
为一边作正方形
,点
恰好与点
重合,则线段
与
的数量关系为
.
(2)
【拓展研究】
在()的条件下,如果正方形
绕点
旋转,连接
,,,线段
与
的数量关系有无变化?请仅就图
的情形给出证明.
(3)
【问题发现】
当正方形
旋转到
,,
三点共线的时候,直接写出线段
的长.
(2020·江苏徐州市)如图,已知点
,,.
(1)
将
绕点
逆时针旋转
得
,画出
,并写出点
的对应点
的坐标为
;
(2)
画出
关于原点成中心对称的图形
,并写出点
的对应点
的坐标为
;
.
(3)
在平面直角坐标系内找点
,使得
,,,
为顶点的四边形为平行四边形,则点
的坐标为
.
(2019·烟台市招远市)明明同学计算
时,他是这样做的:
(1)
明明的解法从第几步开始出现错误,改正后并计算出正确的结果:
(2)
仿照明明的解法,请你计算:.
(2019·广州市越秀区·期末)计算:
(1)
.
(2)
.
第二章有理数及其运算
一、选择题
(2019·无锡市锡山区·期末)如图,在
中,,,,点
是
上的一点,点
是
上的一点,,当
与
中的一个角相等时,则
的值为
A.
或
B.
或
C.
或
D.
或
【答案】D
【解析】
,
,设
,,
①当
时,可得
,
,
,
,
;
②当
时,
如图中,过点
作
,可得
,
,
,
,,
,
,,
,
,
,
,
.
综上所述,.
【知识点】两角分别相等
(2019·天津和平区·模拟)如图,在菱形
中,,,点
是这个菱形内部或边上的一点,若以点
,,
为顶点的三角形是等腰三角形,则
,(,
两点不重合)两点间的最短距离为多少?
A.
B.
C.
D.
【答案】D
【解析】在菱形
中,
,,
,
都是等边三角形.
①若以边
为底,则
垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“,即当点
与点
重合时,
值最小,最小值为
;
②若以边
为底,
为顶角时,以点
为圆心,
长为半径作圆,与
相交于一点,则弧
(除点
外)上的所有点都满足
是等腰三角形,当点
在
上时,
最小,最小值为
;
③若以边
为底,
为顶角,以点
为圆心,
为半径作圆,则弧
上的点
与点
均满足
为等腰三角形,当点
与点
重合时,
最小,显然不满足题意,故此种情况不存在.
综上所述,
的最小值为
.
【知识点】菱形的性质
(2020·湖南湘西土家族苗族自治州·真题)
年中国与“一带一路”沿线国家货物贸易进出口总额达到
亿元,用科学记数法表示
是
A.
B.
C.
D.
【答案】B
【解析】
.
【知识点】正指数科学记数法
(2018·苏州市高新区·模拟)如图,已知
,
是反比例函数
图象上的两点,,交
轴于点
,动点
从坐标原点
出发,沿
匀速运动,终点为
,过点
作
,,垂足分别为
,.设四边形
的面积为
,点
运动的时间为
,则
关于
的函数图象大致为
A.
B.
C.
D.
【答案】A
【解析】①点
在
上运动时,此时四边形
的面积
,保持不变,故排除B、D;
②点
在
上运动时,设路线
的总路程为
,点
的速度为
,则
,
因为
,,
均是常数,
所以
与
成一次函数关系.故排除C.
【知识点】反比例函数系数k的几何意义
(2018·甘肃兰州市·期末)已知
是关于
的方程
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的两条边长,则
的周长为
A.
B.
C.
D.
或
【答案】C
【解析】把
代入方程
得
,解得
,
方程化为
,解得
,,
,不能构造三角形,
三角形三边为
,,,
的周长为
.
【知识点】一元二次方程的根
(2018·沈阳市沈北新区)
,则下面结论中正确的是
A.
没有最小值
B.只有一个
使
有最小值
C.有限个
使
取得最小值
D.有无数多个
使
取得最小值
【答案】D
【解析】
表示数轴上一点
到
,
的距离和,这个距离和的最小值为
,此时
的范围为
,故选:D.
【知识点】绝对值的几何意义
(2019·杭州市上城区·模拟)若关于
的不等式
的解都能使不等式
成立,则
的取值范围是
A.
或
B.
C.
D.
【答案】C
【解析】
关于
的不等式
的解都能使不等式
成立,
,即
,
解不等式
,得:,
则有:,
解得:,
则
的取值范围是
.
故选:C.
【知识点】含参一元一次方程的解法、不等式的性质
(2019·杭州市萧山区)如图,
为
直径
上一动点,过点
的直线交
于
,
两点,且
,
于点
,
于点
,当点
在
上运动时.设
,,下列中图象中,能表示
与
的函数关系式的图象大致是
A.
B.
C.
D.
【答案】A
【解析】点
从点
运动到点
的过程中,
的值逐渐增大,
的长度随
值的变化先变大再变小,当
与
重合时,
有最大值,
,,
时,
过点
,
此时:,,,
所以,随着
的增大,
先增后降,类抛物线.
【知识点】图像法
(2018·石家庄市高邑县·期末)如图,在
中,已知
,,,动点
从点
出发,以
的速度沿线段
向点
运动,在运动过程中,当
为等腰三角形时,点
出发的时刻
可能的值为
A.
B.
或
C.
D.
或
【答案】D
【知识点】等腰三角形的概念
(2020·天津红桥区·模拟)点
,
在数轴上的位置如图所示,其对应的实数分别是
,,下列结论正确的是
A.
B.
C.
D.
【答案】D
【解析】由数轴的定义得:,.
,,则选项A,B均错误;
,
.
,则选项C错误;
,,
,,即
,则选项D正确.
【知识点】绝对值的几何意义
(2018·合肥市长丰县·期末)如图,正方形
的边长为
,动点
,
同时从点
出发,在正方形的边上,分别按
,
的方向,都以
的速度运动,到达点
运动终止,连接
,设运动时间为
,
的面积为
,则下列图象中能大致表示
与
的函数关系的是
A.
B.
C.
D.
【答案】A
【解析】①当
时,
正方形的边长为
,
;
②当
时,
与
之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A选项图象符合.
【知识点】y=ax^2+bx+c的图象
(2020·杭州市拱墅区·模拟)世界上最深的海沟是太平洋的马里亚纳海沟,海拔为
米,数据
用科学记数法表示为
A.
B.
C.
D.
【答案】C
【解析】将
用科学记数法表示为:.
【知识点】正指数科学记数法
(2018·深圳市宝安区·期末)已知有理数
,
在数轴上表示的点如图所示,则下列式子中不正确的是
A.
B.
C.
D.
【答案】C
【解析】
在数轴上的位置可知,,,
A、
,,
,故A选项正确;
B、
,
,故B选项正确;
C、
,
,故C选项错误;
D、
,,
,故D选项正确.
故选C.
【知识点】有理数的乘法
(2019·杭州市萧山区·期末)已知直线
与半径为
的
相切于点
,
是
的一条弦,且
,若
,则直线
与弦
之间的距离为
A.
或
B.
或
C.
或
D.
【答案】A
【解析】连接
,
交
与
.
,
,,
直线
是切线,
,
,
在
中,,
,
同法当弦
在点
下方时,.
【知识点】切线的性质
(2019·浙江温州市·模拟)如图,已知等腰直角三角形
中,,,在
的延长线上任取一点
,过点
作
,使得
,则当点
在
延长线上向左移动时,
的面积大小变化情况是
A.一直变大
B.一直变小
C.先变小再变大
D.先变大再变小
【答案】C
【解析】当
与
的交点在线段
上时,如图
所示.
设
,则
,,则
的面积随
的增大而减小;
当
与
的交点在线段
的延长线上时,如图
所示.
设
,则
,,
,
,即
,
,
,
的面积是:,
的面积随
的增大而增大,
由上可得,
的面积随
的增大先变小后变大.
【知识点】基本定理、k,b对一次函数图象及性质的影响
(2018·苏州市常熟市)直角三角形的两边长为
和
,则此三角形的外接圆半径为
A.
B.
C.
或
D.
或
【答案】D
【解析】由勾股定理可知:
①当
为斜边时,直角三角形的斜边长为:;
②当
为直角边时,直角三角形的斜边长为:;
因此这个三角形的外接圆半径为
或
.
【知识点】三角形的外接圆与外心
(2019·洛阳市汝阳县)已知四个数:,,,,任取其中两个数相乘,所得积的最大值是
A.
B.
C.
D.
【答案】B
【解析】依题意得两个数相乘所得积的最大值是
.
故选B.
【知识点】有理数的乘法
(2021·专项)如图①,点
是
的中点,点
在
上,动点
以每秒
的速度沿图①()的边线运动,运动路径为:,相应的
的面积
关于运动时间
的函数图象如图②,若
,有下列结论:
①图①中的
长是
;
②图②中的
点表示第
秒时,
的值为
;
③图②中的
点表示第
秒时,
的值为
.
其中,正确结论的个数是
A.
B.
C.
D.
【答案】D
【知识点】行程问题
(2019·天津红桥区)已知
,,且
,则
的值为
A.
B.
C.
或
D.
或
【答案】D
【解析】
,
,
,
,
又
,由于
,,而
,,
则
只能取
,
取
或
,
或
.
则
的值为
或
.
【知识点】绝对值的性质
二、填空题
(2019·南通市崇川区·期末)已知射线
,从
点再引射线
,,使
,,则
的度数为
.
【答案】
或
【解析】如图所示.
①
在
,
之间,
,,
②
在
,
之间,
,,
【知识点】角的计算
(2019·济南市槐荫区·期末)已知
,,
位置如图,则化简
.
【答案】
【解析】
由图可知
,,,
,,,
.
【知识点】绝对值的化简、绝对值的几何意义
(2019·株洲市醴陵市·期末)定义:等腰三角形的顶角与其一个底角的度数的比值
称为这个等腰三角形的“特征值”.若等腰
中,,则它的特征值
.
【答案】
或
【解析】①当
为顶角时,等腰三角形两底角的度数为:,
特征值
.
②当
为底角时,顶角的度数为:,
特征值
.
综上所述,特征值
为
或
.
【知识点】等边对等角
(2020·苏州市太仓市·调研)如图,
中,,,,点
是
边上一点,,点
是线段
上的动点,连接
,以
为斜边在
的下方作等腰
,连接
,当
从点
出发运动至点
停止的过程中,
面积的最大值等于
.
【答案】
【解析】设
,
①如图
,当
时,作
于
,
于
,
,
四边形
中,,,
,
,
,
在
和
,
,,,
,
,
,
四边形
是正方形,
设
,则
,得
,即有
,
,,
,
当
时,.
②如图
,
当
时,同理可得
,
当
时,.
综上,当
时,.
【知识点】正方形的概念、二次函数的最值
(2020·单元测试)计算:
()
;
()
;
()
;
()
.
【答案】
;
;
;
【知识点】有理数的加减乘除乘方混合运算
(2018·成都市锦江区)设一组数据:,,,,,我们将前
个数之和记作
,即
,,,,,定义
为这组数据的“嘉祥数”,若
,,,,
这十个数据的“嘉祥数”为
,则
,,,,,
这
个数据的“嘉祥数”为
.
【答案】
【解析】
,
则
嘉祥数为
.
【知识点】有理数的加法法则及计算
(2020·单元测试)如图,圆的周长为
个单位长度.在该圆的
等分点处分别标上数字
,,,,先让圆周上表示数字
的点与数轴上表示数
的点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示数
的点与圆周上表示数字
的点重合.
【答案】
【知识点】数轴的概念
(2020·单元测试)先运用乘法运算律将下列算式变形,再计算出结果.
()
;
()
;
()
;
()
.
【答案】
;
;
;
;
;
;
;
【知识点】有理数的乘法
(2019·洛阳市汝阳县)某景点
月
日的最低气温为
,最高气温为
,那么该景点这天的是温差是
.
【答案】
【解析】
.
【知识点】有理数减法的应用
三、解答题
(2018·保定市定州市)计算:
【知识点】有理数的加减乘除乘方混合运算、有理数加减乘除混合运算
(1)
;
【答案】
(2)
;
【答案】
(3)
.
【答案】
(2019·济南市天桥区)按要求作答.
【知识点】两角分别相等、正方形的性质
(1)
【问题发现】
如图
,在
中,,,点
为
的中点,以
为一边作正方形
,点
恰好与点
重合,则线段
与
的数量关系为
.
【答案】
【解析】在
中,,
根据勾股定理得,,
点
为
的中点,
,
四边形
是正方形,
,
,
.
(2)
【拓展研究】
在()的条件下,如果正方形
绕点
旋转,连接
,,,线段
与
的数量关系有无变化?请仅就图
的情形给出证明.
【答案】无变化;
如图
,在
中,,
,
,
在正方形
中,,
在
中,,
,
,
,
,
,
,
,
线段
与
的数量关系无变化.
(3)
【问题发现】
当正方形
旋转到
,,
三点共线的时候,直接写出线段
的长.
【答案】
或
【解析】当点
在线段
上时,如图
,
由()知,,
在
中,,,
根据勾股定理得,,
,
由()知,,
,
当点
在线段
的延长线上时,如图
,
在
中,,
,
,
在正方形
中,,
在
中,,
,
,
,
,
,
,
,
由()知,,
在
中,,,
根据勾股定理得,,
,
由()知,,
.
即:当正方形
旋转到
,,
三点共线时候,线段
的长为
或
.
(2020·江苏徐州市)如图,已知点
,,.
【知识点】坐标平面内图形的旋转变换、平行四边形及其性质
(1)
将
绕点
逆时针旋转
得
,画出
,并写出点
的对应点
的坐标为
;
【答案】如图,
即为所求.
【解析】点
的坐标为
.
故答案为
.
(2)
画出
关于原点成中心对称的图形
,并写出点
的对应点
的坐标为
;
【答案】
即为所求.
【解析】点
的坐标为
.
故答案为
.
(3)
在平面直角坐标系内找点
,使得
,,,
为顶点的四边形为平行四边形,则点
的坐标为
.
【答案】
或
或
【解析】如图,满足条件的点
的坐标为
或
或
.
故答案为
或
或
.
(2019·烟台市招远市)明明同学计算
时,他是这样做的:
【知识点】有理数加减混合运算
(1)
明明的解法从第几步开始出现错误,改正后并计算出正确的结果:
【答案】明明的解法从第三步开始出现错误,
改正:
(2)
仿照明明的解法,请你计算:.
【答案】
(2019·广州市越秀区·期末)计算:
【知识点】有理数的加减乘除乘方混合运算、有理数加减混合运算
(1)
.
【答案】
(2)
.
【答案】
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
