3.2直线的方程(3课时)
图片预览


文档简介
(共15张PPT)
3.2.1 直线的点斜式方程
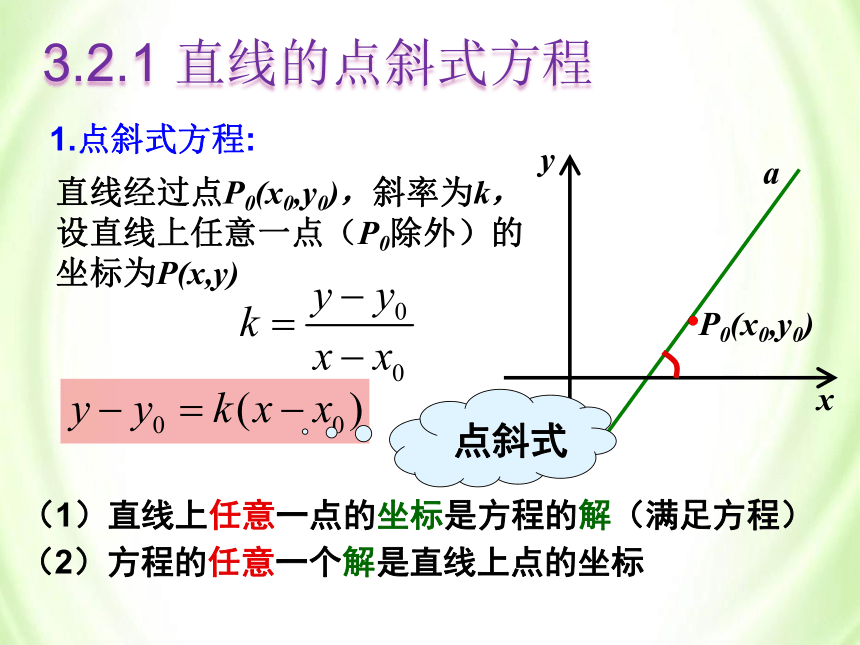
1.点斜式方程:
x
y
(1)直线上任意一点的坐标是方程的解(满足方程)
a
P0(x0,y0)
直线经过点P0(x0,y0),斜率为k,设直线上任意一点(P0除外)的坐标为P(x,y)
(2)方程的任意一个解是直线上点的坐标
点斜式
x
y
l
P0(x0,y0)
y0
O
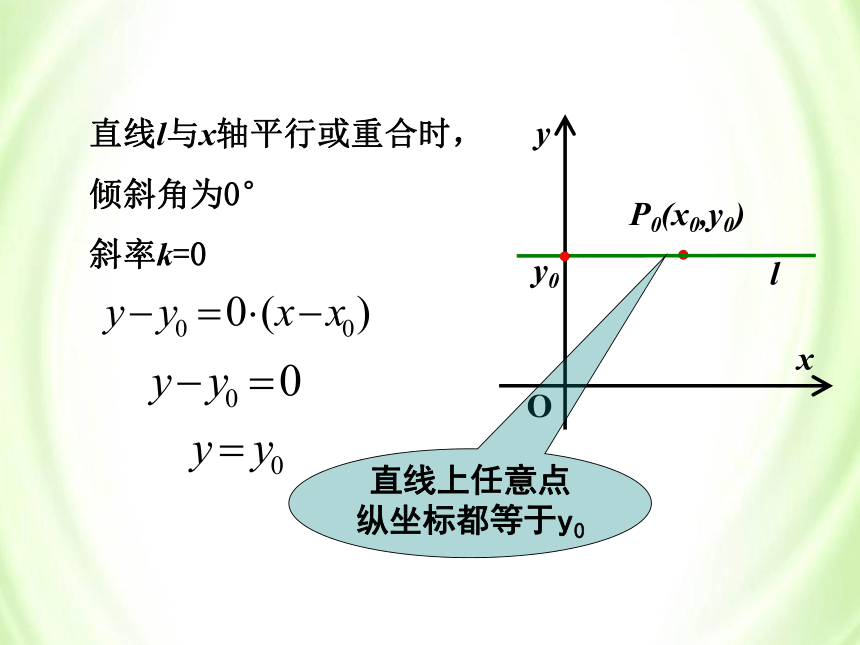
直线l与x轴平行或重合时,
倾斜角为0°
斜率k=0
直线上任意点
纵坐标都等于y0
x
y
l
P0(x0,y0)
x0
O
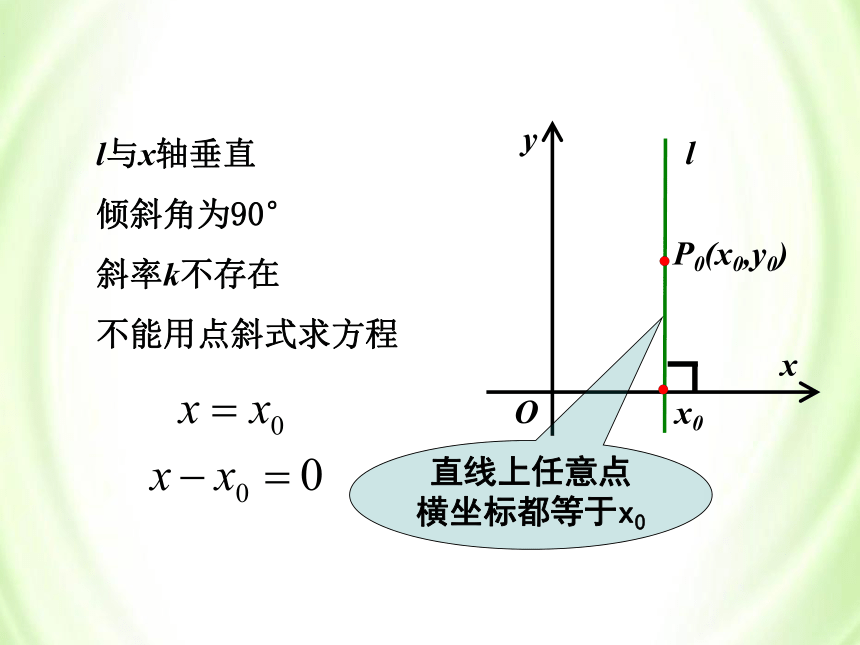
l与x轴垂直
倾斜角为90°
斜率k不存在
不能用点斜式求方程
直线上任意点
横坐标都等于x0
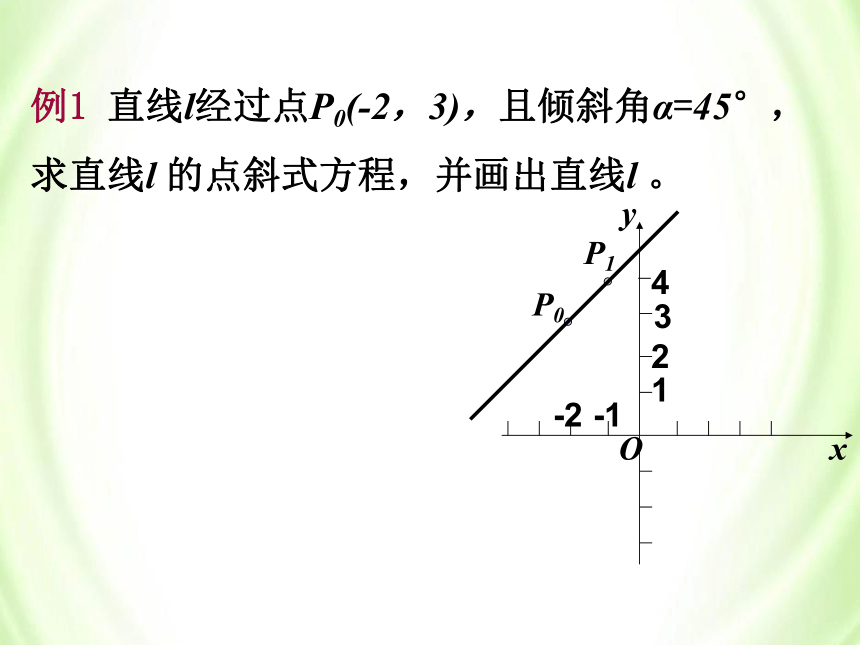
例1 直线l经过点P0(-2,3),且倾斜角α=45°,
求直线l 的点斜式方程,并画出直线l 。
O
x
y
-1
-2
1
2
3
4
P0
P1
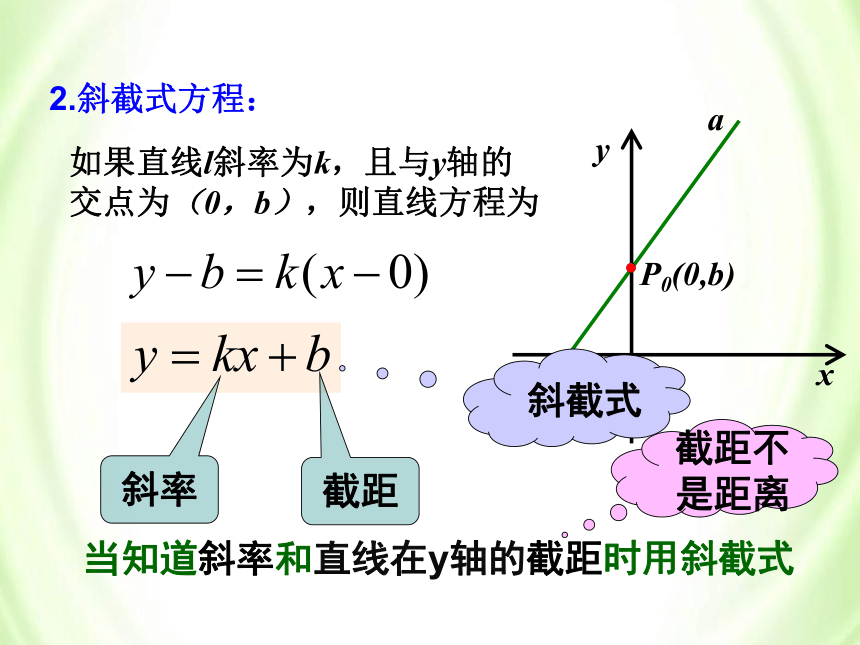
2.斜截式方程:
x
y
a
P0(0,b)
如果直线l斜率为k,且与y轴的交点为(0,b),则直线方程为
斜率
截距
斜截式
当知道斜率和直线在y轴的截距时用斜截式
截距不是距离
例2 已知直线l1:y=k1x+b1, l2:y=k2x+b2,试讨论:(1) l1 //l2 的条件是什么?(2)l1 ⊥ l2的条件是什么?
解:(1)k1=k2且b1≠b2
(2)k1k2=-1
3.2.2 直线的两点式方程
1.两点式方程:
直线经过点P1(x1,y1), P2(x2,y2)(x1≠x2 ,y1 ≠y2)
x
y
l
P2(x2,y2)
P1(x1,y1)
点斜式列方程
两点式
2.截距式方程:
x
y
l
A(a,0)
B(0,b)
a为直线在x轴上的截距
b为直线在y轴上的截距
代入两点式方程得
横截距
纵截距
截距式
例4 三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC、AC边所在两条直线的方程,以及BC边上中线所在
直线的方程.
x
y
O
.
M
B
.
A
.
.
C
解: 直线BC用两点式可得方程5x+3y-6=0
直线AC用截距式可得方程
∴
∴直线AM用两点式可得方程x+13y+5=0
若A(x1,y1), B(x2,y2),求线段AB
垂直平分线的方程的步骤:
第一步:求线段AB中点坐标M( , )
x1+x2
2
y1+y2
2
第二步:求斜率
第三步:点斜式列方程
3.2.3 直线的一般式方程
我们共学习了几种直线方程的形式
点斜式
斜截式
两点式
截距式
直线l与x轴平行或重合时,倾斜角为0°,斜率k=0,直线方程为:
直线l与x轴垂直时,倾斜角为90°,斜率k不存在,直线方程为:
以上这些直线方程都是关于x,y的
几元几次方程?
二元一次
直线的一般式方程:
,其中A,B不同时为0
一般式
①当B≠0时
②当B=0时
,是垂直于x轴的一条直线
注意 对于直线方程的一般式,一般作如下约定:
1)x的系数为正,
2)x,y的系数及常数项一般不出现分数,
3)一般按含x项,含y项、常数项顺序排列.
③当A=0时
,是平行于x轴的一条直线
例5 已知直线经过点A(6,- 4),斜率为 ,
求直线的点斜式和一般式方程。
例6 把直线l的一般式方程x-2y+6=0化成斜截式,
求直线l的斜率以及它在x轴与y轴上的截距,
并画出图形。
3.2.1 直线的点斜式方程
1.点斜式方程:
x
y
(1)直线上任意一点的坐标是方程的解(满足方程)
a
P0(x0,y0)
直线经过点P0(x0,y0),斜率为k,设直线上任意一点(P0除外)的坐标为P(x,y)
(2)方程的任意一个解是直线上点的坐标
点斜式
x
y
l
P0(x0,y0)
y0
O
直线l与x轴平行或重合时,
倾斜角为0°
斜率k=0
直线上任意点
纵坐标都等于y0
x
y
l
P0(x0,y0)
x0
O
l与x轴垂直
倾斜角为90°
斜率k不存在
不能用点斜式求方程
直线上任意点
横坐标都等于x0
例1 直线l经过点P0(-2,3),且倾斜角α=45°,
求直线l 的点斜式方程,并画出直线l 。
O
x
y
-1
-2
1
2
3
4
P0
P1
2.斜截式方程:
x
y
a
P0(0,b)
如果直线l斜率为k,且与y轴的交点为(0,b),则直线方程为
斜率
截距
斜截式
当知道斜率和直线在y轴的截距时用斜截式
截距不是距离
例2 已知直线l1:y=k1x+b1, l2:y=k2x+b2,试讨论:(1) l1 //l2 的条件是什么?(2)l1 ⊥ l2的条件是什么?
解:(1)k1=k2且b1≠b2
(2)k1k2=-1
3.2.2 直线的两点式方程
1.两点式方程:
直线经过点P1(x1,y1), P2(x2,y2)(x1≠x2 ,y1 ≠y2)
x
y
l
P2(x2,y2)
P1(x1,y1)
点斜式列方程
两点式
2.截距式方程:
x
y
l
A(a,0)
B(0,b)
a为直线在x轴上的截距
b为直线在y轴上的截距
代入两点式方程得
横截距
纵截距
截距式
例4 三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC、AC边所在两条直线的方程,以及BC边上中线所在
直线的方程.
x
y
O
.
M
B
.
A
.
.
C
解: 直线BC用两点式可得方程5x+3y-6=0
直线AC用截距式可得方程
∴
∴直线AM用两点式可得方程x+13y+5=0
若A(x1,y1), B(x2,y2),求线段AB
垂直平分线的方程的步骤:
第一步:求线段AB中点坐标M( , )
x1+x2
2
y1+y2
2
第二步:求斜率
第三步:点斜式列方程
3.2.3 直线的一般式方程
我们共学习了几种直线方程的形式
点斜式
斜截式
两点式
截距式
直线l与x轴平行或重合时,倾斜角为0°,斜率k=0,直线方程为:
直线l与x轴垂直时,倾斜角为90°,斜率k不存在,直线方程为:
以上这些直线方程都是关于x,y的
几元几次方程?
二元一次
直线的一般式方程:
,其中A,B不同时为0
一般式
①当B≠0时
②当B=0时
,是垂直于x轴的一条直线
注意 对于直线方程的一般式,一般作如下约定:
1)x的系数为正,
2)x,y的系数及常数项一般不出现分数,
3)一般按含x项,含y项、常数项顺序排列.
③当A=0时
,是平行于x轴的一条直线
例5 已知直线经过点A(6,- 4),斜率为 ,
求直线的点斜式和一般式方程。
例6 把直线l的一般式方程x-2y+6=0化成斜截式,
求直线l的斜率以及它在x轴与y轴上的截距,
并画出图形。
