2.2 等差数列 (2) 课件
文档属性
| 名称 | 2.2 等差数列 (2) 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 890.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-27 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
第二课时
知识与技能
(1)掌握“判断数列是否为等差数列”常用的方法;
(2)探索并掌握等差数列的另外两个通项公式;
(3)进一步熟练掌握等差数列的性质及应用。
过程与方法
通过对一列数的观察、归纳,写出符合条件的一个通项公式,培养学生的观察能力和抽象概括能力.
情感态度与价值观
通过本节课的学习,体会数学来源于生活,提高数学学习的兴趣。
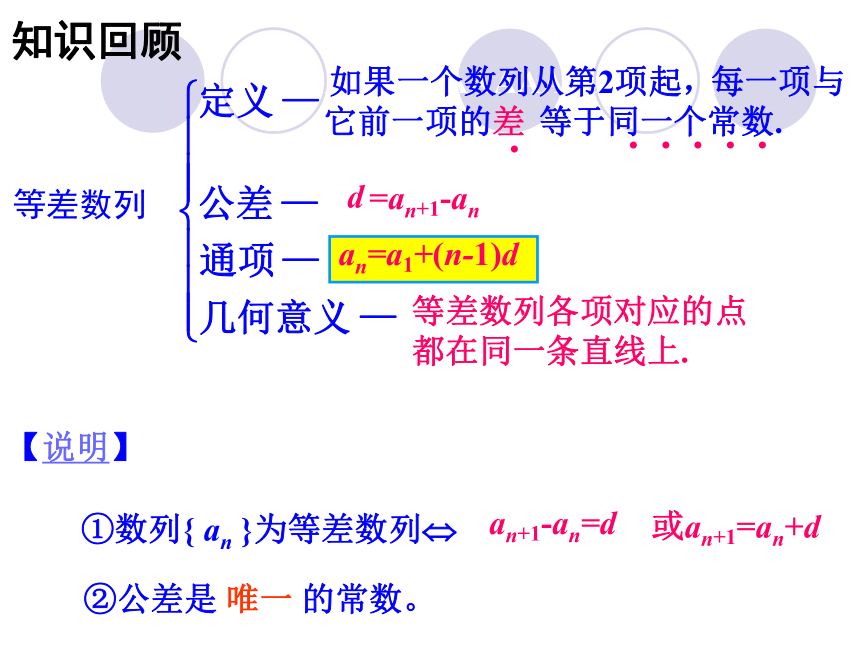
知识回顾
等差数列
AAAAAAAAAAAAA 每一项与
它前一项的差
如果一个数列从第2项起,
等于同一个常数.
.
. . . . .
【说明】
AAA①数列{ an }为等差数列
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是 唯一 的常数。
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
例1 已知数列 的通项公式为 ,其中p,q为常数,且 ,那么这个数列一定是等差数列吗?
分析:判断 是不是等差数列,可以利用等差数列的定义,也就 是看 是不是一个与n无关的常数
解:取数列
中的任意相邻两项
求差得
它是一个与n无关的数,所以 是等差数列
想一想还可以怎么证?
自主探究一 等差数列的判定方法
结论:如果一个数列的通项公式是关于正整数n的
一次函数, 那么这个数列一定是等差数列
等差数列的通项公式为:
直线的一般形式:
(一次项系数)
(系数之和)
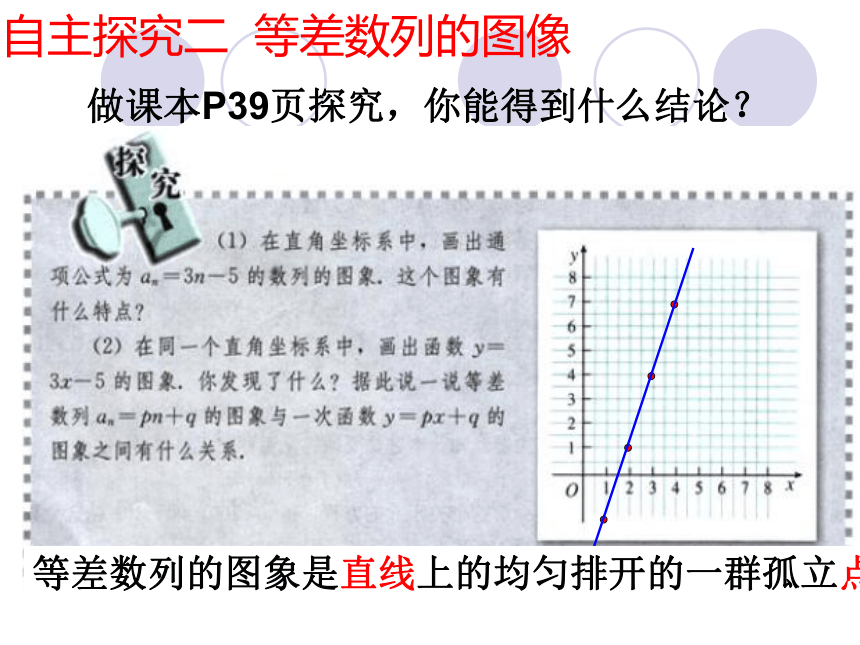
自主探究二 等差数列的图像
做课本P39页探究,你能得到什么结论?
等差数列的图象是直线上的均匀排开的一群孤立点
①当p不为零时,等差数列的图象是直线y=px+q上的均匀排开的一群孤立的点。
②当p为零时,等差数列的图象是平行于x轴的直线(或x轴)上的均匀分布的一群孤立的点。
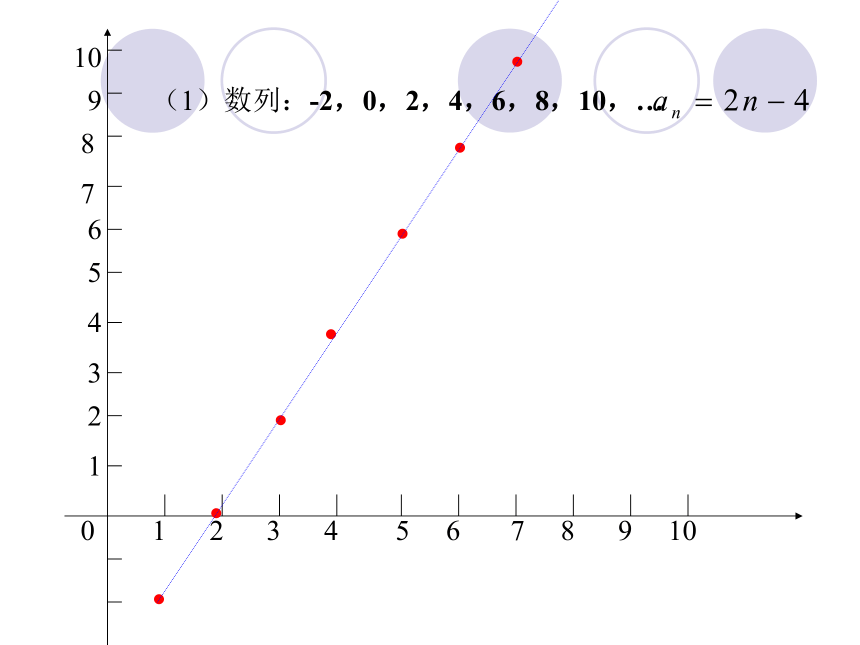
自主探究二 等差数列的图像
做课本P39页探究,你能得到什么结论?
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
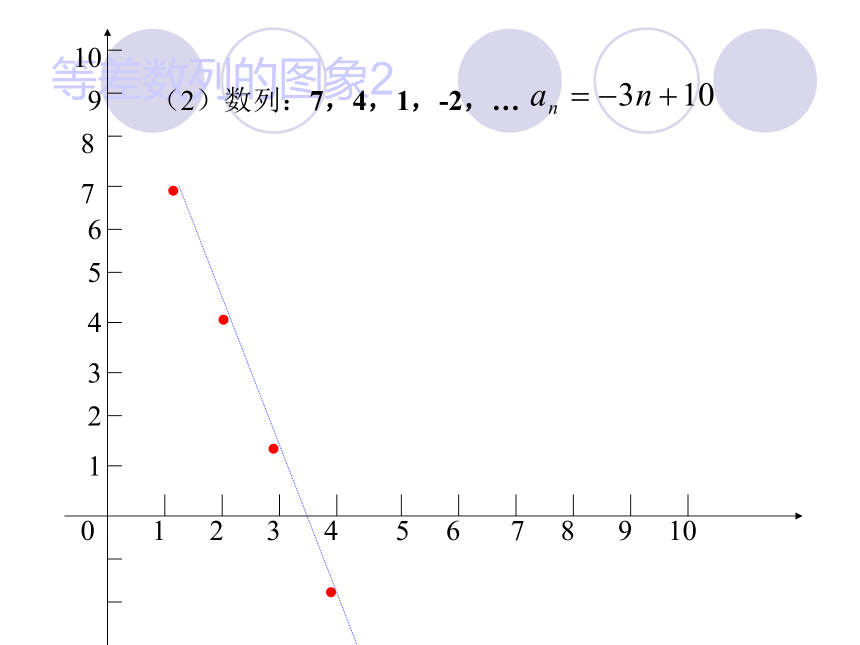
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
等差数列的图象3
(1)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
小结:判定等差数列常用的方法有:
(1)定义法:利用 ,
(2)等差中项法:数列为非常数列时,也可利用
(3)
( , 为常数, )
是等差数列
在等差数列
的各项中,与
首末两项等距
离的两项和等
于首末两项的
和
特例:若
则
自主探究三 等差数列的性质
解:由 a1+a20 =a6+ a15 = a9 +a12
及 a6+a9+a12+a15=20,可得a1+a20=10
(2) 已知 a6+a9+a12+a15=20,求a1+a20
在等差数列{an}中:
(1)已知 ,求
解:∵
∴
练习:
(3)已知 a1+a4+a7 =15, a2a4a6=45, 求数列的通
项公式
解: ∵
∴
∴
∴
解得 或
若 ,则 ,∴
同理可得
小结: 等差数列的性质
1. an= ,d=
am+(n - m) d
2.在等差数列{an}中,由 m+n=p+q
am+an=ap+aq
4.等差数列{an}每隔一定距离抽取一项所组成的数列
仍成等差数列. 例如: a1、 a3 、 a5 、 a7 、 …仍成
等差数列, a7 、 a14 、 a21 、…. 、 a7m 、…仍成等
差数列
5.数列 ( , 为常数)仍成等差数列
6. 和 均为等差数列,则 也成等差数列
如果数列{an}是等差数列,则an=kn+b,其中k,b均
为常数。反之,如果数列{an}是an=kn+b,则数列{an}
是等差数列
题型一 等差数列的定义及应用
[例1] 已知数列 的通项公式为
,试问该数列是否为等差数列
分析:利用等差数列的定义即可
解:∵数列 的通项公式为
∴
∴该数列为等差数列
题型二 等差数列的通项
[例2] 两个等差数列5,8,11,…和
3,7,11,…都有100项,问它们
有多少个共同的项?
解法一: 设两个数列分别为
则
设数列 的第 项与 的第 项相同
即
即
∵
∴ 必须为3的倍数,设
由条件知
又∵ ,∴
∴共有25个共同的项
解法二:由解法一知两数列的通项公式分别
为 ,
设共同项构成新数列 ,则
由于数列 , 为等差数列,
∴数列 仍成等差数列,且公差为
∴
又∵ ,
∴
∴ ,知数列有25个共同项
[例3] 等差数列 中, ,
,求
题型三 等差数列的性质应用
解:∵
∴
∵
∴
∴
[变式练习] 若 ,数列 和
各自成等差数列,求
解: 由
得
[例4] 已知成等差数列的四个数之和为 26,第二个数和第三个数之积为40,求这个等差数列.
题型四 创新、拓展、实践
解:设四个数为
∴四个数为2,5,8,11或11,8,5,2.
则
解得:
或
[例6]等差数列 的公差为 ,
试比较 与 的大小
解:设
∴
(1)通项法:设数列的通项公式,即设
等差数列通项的设法
(2)对称项设法:当等差数列{an}的项数为奇数时,可设
中间一项为a,再以公差为d向两边分别设项为:
…,a-2d,a-d,a,a+d,a+2d,…
当等差数列{an}的项数为偶数时,可设中间两项分别为a-d,a+d,再以公差为2d向两边分别设项为,
…,a-3d,a-d,a+d,a+3d,…
对称项设法的优点:若有n个数构成等差数列.利用对称项设出这个数列,则其各项和为na.
梯子的最高一级宽33cm,最低一级宽110,中间
还有10级,各级的宽度成等差数列.
计算中间各级的宽.
解:设 表示梯子自上而下各级宽度所成的等差数列,由知己条件,可知
得
所以
即
因此
第二课时
知识与技能
(1)掌握“判断数列是否为等差数列”常用的方法;
(2)探索并掌握等差数列的另外两个通项公式;
(3)进一步熟练掌握等差数列的性质及应用。
过程与方法
通过对一列数的观察、归纳,写出符合条件的一个通项公式,培养学生的观察能力和抽象概括能力.
情感态度与价值观
通过本节课的学习,体会数学来源于生活,提高数学学习的兴趣。
知识回顾
等差数列
AAAAAAAAAAAAA 每一项与
它前一项的差
如果一个数列从第2项起,
等于同一个常数.
.
. . . . .
【说明】
AAA①数列{ an }为等差数列
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是 唯一 的常数。
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
例1 已知数列 的通项公式为 ,其中p,q为常数,且 ,那么这个数列一定是等差数列吗?
分析:判断 是不是等差数列,可以利用等差数列的定义,也就 是看 是不是一个与n无关的常数
解:取数列
中的任意相邻两项
求差得
它是一个与n无关的数,所以 是等差数列
想一想还可以怎么证?
自主探究一 等差数列的判定方法
结论:如果一个数列的通项公式是关于正整数n的
一次函数, 那么这个数列一定是等差数列
等差数列的通项公式为:
直线的一般形式:
(一次项系数)
(系数之和)
自主探究二 等差数列的图像
做课本P39页探究,你能得到什么结论?
等差数列的图象是直线上的均匀排开的一群孤立点
①当p不为零时,等差数列的图象是直线y=px+q上的均匀排开的一群孤立的点。
②当p为零时,等差数列的图象是平行于x轴的直线(或x轴)上的均匀分布的一群孤立的点。
自主探究二 等差数列的图像
做课本P39页探究,你能得到什么结论?
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
等差数列的图象3
(1)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
小结:判定等差数列常用的方法有:
(1)定义法:利用 ,
(2)等差中项法:数列为非常数列时,也可利用
(3)
( , 为常数, )
是等差数列
在等差数列
的各项中,与
首末两项等距
离的两项和等
于首末两项的
和
特例:若
则
自主探究三 等差数列的性质
解:由 a1+a20 =a6+ a15 = a9 +a12
及 a6+a9+a12+a15=20,可得a1+a20=10
(2) 已知 a6+a9+a12+a15=20,求a1+a20
在等差数列{an}中:
(1)已知 ,求
解:∵
∴
练习:
(3)已知 a1+a4+a7 =15, a2a4a6=45, 求数列的通
项公式
解: ∵
∴
∴
∴
解得 或
若 ,则 ,∴
同理可得
小结: 等差数列的性质
1. an= ,d=
am+(n - m) d
2.在等差数列{an}中,由 m+n=p+q
am+an=ap+aq
4.等差数列{an}每隔一定距离抽取一项所组成的数列
仍成等差数列. 例如: a1、 a3 、 a5 、 a7 、 …仍成
等差数列, a7 、 a14 、 a21 、…. 、 a7m 、…仍成等
差数列
5.数列 ( , 为常数)仍成等差数列
6. 和 均为等差数列,则 也成等差数列
如果数列{an}是等差数列,则an=kn+b,其中k,b均
为常数。反之,如果数列{an}是an=kn+b,则数列{an}
是等差数列
题型一 等差数列的定义及应用
[例1] 已知数列 的通项公式为
,试问该数列是否为等差数列
分析:利用等差数列的定义即可
解:∵数列 的通项公式为
∴
∴该数列为等差数列
题型二 等差数列的通项
[例2] 两个等差数列5,8,11,…和
3,7,11,…都有100项,问它们
有多少个共同的项?
解法一: 设两个数列分别为
则
设数列 的第 项与 的第 项相同
即
即
∵
∴ 必须为3的倍数,设
由条件知
又∵ ,∴
∴共有25个共同的项
解法二:由解法一知两数列的通项公式分别
为 ,
设共同项构成新数列 ,则
由于数列 , 为等差数列,
∴数列 仍成等差数列,且公差为
∴
又∵ ,
∴
∴ ,知数列有25个共同项
[例3] 等差数列 中, ,
,求
题型三 等差数列的性质应用
解:∵
∴
∵
∴
∴
[变式练习] 若 ,数列 和
各自成等差数列,求
解: 由
得
[例4] 已知成等差数列的四个数之和为 26,第二个数和第三个数之积为40,求这个等差数列.
题型四 创新、拓展、实践
解:设四个数为
∴四个数为2,5,8,11或11,8,5,2.
则
解得:
或
[例6]等差数列 的公差为 ,
试比较 与 的大小
解:设
∴
(1)通项法:设数列的通项公式,即设
等差数列通项的设法
(2)对称项设法:当等差数列{an}的项数为奇数时,可设
中间一项为a,再以公差为d向两边分别设项为:
…,a-2d,a-d,a,a+d,a+2d,…
当等差数列{an}的项数为偶数时,可设中间两项分别为a-d,a+d,再以公差为2d向两边分别设项为,
…,a-3d,a-d,a+d,a+3d,…
对称项设法的优点:若有n个数构成等差数列.利用对称项设出这个数列,则其各项和为na.
梯子的最高一级宽33cm,最低一级宽110,中间
还有10级,各级的宽度成等差数列.
计算中间各级的宽.
解:设 表示梯子自上而下各级宽度所成的等差数列,由知己条件,可知
得
所以
即
因此
