(试题6)高中数学苏教版选修1-1综合测试
文档属性
| 名称 | (试题6)高中数学苏教版选修1-1综合测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 108.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-27 16:26:03 | ||
图片预览



文档简介
选修1-1综合测试
一、选择题:本大题每小题5分,共60分,在每小题给出的四个选项中,只有
一个选项是符合题目要求的。
1.某食品的广告词为:“幸福的人们都拥有”。初听起来,这似乎只是普通的
的赞美说辞,可实际上它的宣传效果很大,吸引消费者争相购买。那么,该
广告词的等价命题是( )
A.不拥有的人们不一定幸福 B.不拥有的人们可能幸福
C.拥有的人们不一定幸福 D. 不拥有的人们不幸福
2.“两个三角形相似”的一个充分不必要条件是( )
A.它们的面积相等 B.它们的三边对应成比例
C.这两个三角形全等 D.这两个三角形有两个角对应相等
3.若双曲线和椭圆的离心率互为倒
数,则以、、为边长的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
4.如果椭圆上一点P到它右焦点的距离为10,那么,点P到它的
左准线的距离是( )
A.10 B.6 C.4 D.
5.抛物线的焦点坐标是( )
A. B. C.或 D.
6.“”是方程“表示双曲线”的( )
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.都不是
7.函数的导数是( )
A. B.
C. D.
8.已知定义在上的奇函数的导函数,则满足
的实数的取值范围是( )
A. B. C. D.
9.已知函数在处有极值4,则( )
A.6 B.6或11 C.11 D.0或6
10.下列结论中,正确的是( )
①“且为真”是“或为真”的充分不必要条件
②“且为假”是“或为假”的充分不必要条件
③“且为真”是“非为假”的必要不充分条件
④“非为真”是“或为假”的必要不充分条件
A.①② B.①④ C.②④ D.③④
11.若函数在处可导,且,则等于( )
A. B. C.3 D.2
12.设为抛物线的焦点,A、B、C为该抛物线上三点,若,
则( )
A.9 B.6 C.4 D.3
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.椭圆的离心率为,则的值为 。
14.过双曲线的左焦点且垂直于轴的直线与双曲线相交于、
两点,以为直径的圆恰好过双曲线的右顶点,则双曲线的离心率为 。
15.曲线的切线中,斜率最小的切线方程为 。
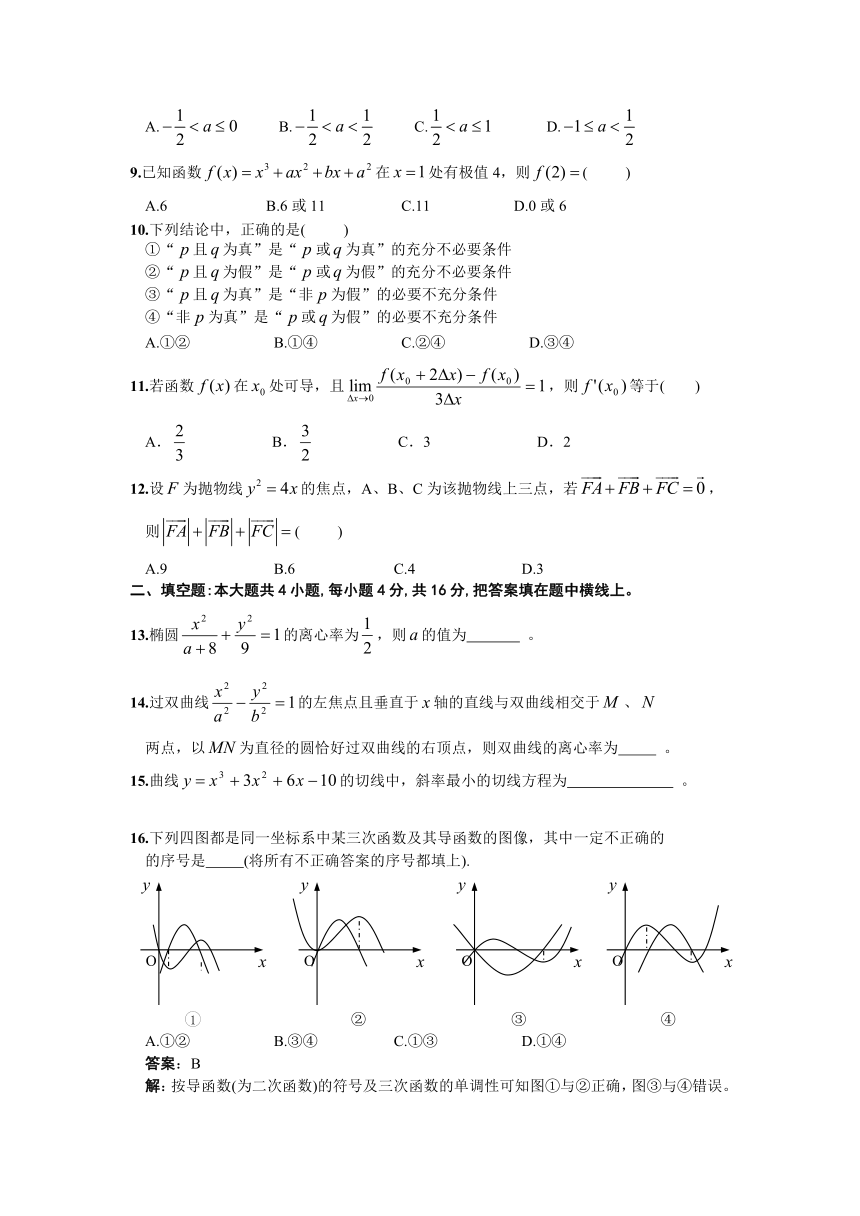
16.下列四图都是同一坐标系中某三次函数及其导函数的图像,其中一定不正确的
的序号是 (将所有不正确答案的序号都填上).
A.①② B.③④ C.①③ D.①④
答案:B
解:按导函数(为二次函数)的符号及三次函数的单调性可知图①与②正确,图③与④错误。
三、解答题:本大题共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
若、是实数,求使且成立的充要条件。
18.(本小题满分12分)
设连结双曲线与的四个顶点的四边形面积为,四个
焦点的四边形面积为,求的最大值。
19.(本小题满分12分)
边长为的正方形铁皮,四角各截去边长为的正方形后折成一只无盖的盒子,
问等于多少时,盒子的容积最大?最大容积是多少?
20.(本小题满分12分)
已知椭圆的中心在原点,焦点在轴上,离心率为,它与直线相
交于P、Q两点,若,求椭圆方程。
21.(本小题满分12分)
如图,已知梯形ABCD中,点E分
有向线段所成的比为,双曲线过C、D、
E三点,且以A、B为焦点。求双曲线离心率的
值。
22.(本小题满分14分)
已知,,极大值为1,极小值为-1,求、的值.
参考答案
1.答案:D
解:因为该广告词的等价命题就是该广告词的逆否命题。故选D。
2.答案:C
解:答案A是非充分非必要条件;答案B、D是充要条件;答案C是充分不必要条件。故选C。
3.答案:B
解:由已知得,解得,,可知,以、、为边长的三角形是直角三角形。故选B
4.答案:D
解:由椭圆的第一定义可知,点P到它左焦点的距离为6,而椭圆的离心率为,于是由椭圆的第二定义,可知点P到左准线的距离为。故选D。
5.答案:A
解:将化为,可知,,。故选A。
6.答案:A
解:当方程表示双曲线时,;当时,若,则方程表示两条相交直线,只有在且时,方程才表示双曲线。故选A。
7.答案:B
解: , 。故选B。
8.答案:C
解: , 在上是增函数,又是奇函数,
可化为,即。
得。故选C。
9.答案:B
解: 函数在处有极值4, ,即,
解得 或 。 或。
故或。
10.答案:B
解:“且为真”时,“或为真”成立,反之,“或为真”时,
“且为真”不一定成立。 ①正确;
“且为假”是“或为假”的充分必要条件, ②不正确;
“且为真”时,“非为假”成立, ③不正确;
“非为真”时,“或为假”不成立,反之,“或为假”时,
“非为真”成立, ④正确。故选B。
11.解:
, 。故选B。
12.答案:B
解:易求得抛物线的焦点F的坐标为,准线为,设、、,则, , ,可得,从而,6,故选B。
13.答案:
解: 椭圆的离心率为, 或 。
解得 或。
14.答案:2
解:点、的横坐标为,代入得,、的纵坐标分别为。 ,于是半径,而该圆恰好过双曲线的右顶点, 。即,就是,整理为,解得。
15.答案:
解: , 当时,,此时,切点为,切线方程为,即。
16.答案:B
解:按导函数(为二次函数)的符号及三次函数的单调性可知图①与②正确,图③与④错误。
三、解答题:本大题共74分,解答应写出文字说明,证明过程或演算步骤。
17.解:①(先寻找必要条件)若且,则且,得,而,。
②(再证明上面所求得的必要条件又是充分条件)若,则、,从而=,得。
故当、为实数时,使且成立的充要条件为。
18.解: 四个顶点为, ;
四个焦点为, 。
=(当且仅当时“=”号成立)。
故的最大值为。
19.解:设铁盒的容积为V,则
,由及,得。令,得(舍去)或。 时,;而时,。时,。
20.解: , ,即椭圆方程为,
设、,由得
,,于是,
,
,即,得,解得。故所求椭圆方程为。
21.解:建系如图,设,,其中
为双曲线的半焦距,是梯形的高。
由定比分点坐标公式得,
设双曲线方程为,则离心率。
将C、E的坐标和代入双曲线方程得,
① ②
由①得,代入②并整理得,。故为所求双曲线的离心率。
22.解:求得,
极大值为1,极小值为-1,
(*)有二根,且。 ①
又,即 ②,
,即 ③
②+③得 ④
①入④并整理得, 。 =0。
将代入(*)得,而, ,代入②得=2。
故=2,=0为所求。
O
O
O
O
②
③
④
E
D
C
B
A
E
D
C
B
A
O
一、选择题:本大题每小题5分,共60分,在每小题给出的四个选项中,只有
一个选项是符合题目要求的。
1.某食品的广告词为:“幸福的人们都拥有”。初听起来,这似乎只是普通的
的赞美说辞,可实际上它的宣传效果很大,吸引消费者争相购买。那么,该
广告词的等价命题是( )
A.不拥有的人们不一定幸福 B.不拥有的人们可能幸福
C.拥有的人们不一定幸福 D. 不拥有的人们不幸福
2.“两个三角形相似”的一个充分不必要条件是( )
A.它们的面积相等 B.它们的三边对应成比例
C.这两个三角形全等 D.这两个三角形有两个角对应相等
3.若双曲线和椭圆的离心率互为倒
数,则以、、为边长的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
4.如果椭圆上一点P到它右焦点的距离为10,那么,点P到它的
左准线的距离是( )
A.10 B.6 C.4 D.
5.抛物线的焦点坐标是( )
A. B. C.或 D.
6.“”是方程“表示双曲线”的( )
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.都不是
7.函数的导数是( )
A. B.
C. D.
8.已知定义在上的奇函数的导函数,则满足
的实数的取值范围是( )
A. B. C. D.
9.已知函数在处有极值4,则( )
A.6 B.6或11 C.11 D.0或6
10.下列结论中,正确的是( )
①“且为真”是“或为真”的充分不必要条件
②“且为假”是“或为假”的充分不必要条件
③“且为真”是“非为假”的必要不充分条件
④“非为真”是“或为假”的必要不充分条件
A.①② B.①④ C.②④ D.③④
11.若函数在处可导,且,则等于( )
A. B. C.3 D.2
12.设为抛物线的焦点,A、B、C为该抛物线上三点,若,
则( )
A.9 B.6 C.4 D.3
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.椭圆的离心率为,则的值为 。
14.过双曲线的左焦点且垂直于轴的直线与双曲线相交于、
两点,以为直径的圆恰好过双曲线的右顶点,则双曲线的离心率为 。
15.曲线的切线中,斜率最小的切线方程为 。
16.下列四图都是同一坐标系中某三次函数及其导函数的图像,其中一定不正确的
的序号是 (将所有不正确答案的序号都填上).
A.①② B.③④ C.①③ D.①④
答案:B
解:按导函数(为二次函数)的符号及三次函数的单调性可知图①与②正确,图③与④错误。
三、解答题:本大题共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
若、是实数,求使且成立的充要条件。
18.(本小题满分12分)
设连结双曲线与的四个顶点的四边形面积为,四个
焦点的四边形面积为,求的最大值。
19.(本小题满分12分)
边长为的正方形铁皮,四角各截去边长为的正方形后折成一只无盖的盒子,
问等于多少时,盒子的容积最大?最大容积是多少?
20.(本小题满分12分)
已知椭圆的中心在原点,焦点在轴上,离心率为,它与直线相
交于P、Q两点,若,求椭圆方程。
21.(本小题满分12分)
如图,已知梯形ABCD中,点E分
有向线段所成的比为,双曲线过C、D、
E三点,且以A、B为焦点。求双曲线离心率的
值。
22.(本小题满分14分)
已知,,极大值为1,极小值为-1,求、的值.
参考答案
1.答案:D
解:因为该广告词的等价命题就是该广告词的逆否命题。故选D。
2.答案:C
解:答案A是非充分非必要条件;答案B、D是充要条件;答案C是充分不必要条件。故选C。
3.答案:B
解:由已知得,解得,,可知,以、、为边长的三角形是直角三角形。故选B
4.答案:D
解:由椭圆的第一定义可知,点P到它左焦点的距离为6,而椭圆的离心率为,于是由椭圆的第二定义,可知点P到左准线的距离为。故选D。
5.答案:A
解:将化为,可知,,。故选A。
6.答案:A
解:当方程表示双曲线时,;当时,若,则方程表示两条相交直线,只有在且时,方程才表示双曲线。故选A。
7.答案:B
解: , 。故选B。
8.答案:C
解: , 在上是增函数,又是奇函数,
可化为,即。
得。故选C。
9.答案:B
解: 函数在处有极值4, ,即,
解得 或 。 或。
故或。
10.答案:B
解:“且为真”时,“或为真”成立,反之,“或为真”时,
“且为真”不一定成立。 ①正确;
“且为假”是“或为假”的充分必要条件, ②不正确;
“且为真”时,“非为假”成立, ③不正确;
“非为真”时,“或为假”不成立,反之,“或为假”时,
“非为真”成立, ④正确。故选B。
11.解:
, 。故选B。
12.答案:B
解:易求得抛物线的焦点F的坐标为,准线为,设、、,则, , ,可得,从而,6,故选B。
13.答案:
解: 椭圆的离心率为, 或 。
解得 或。
14.答案:2
解:点、的横坐标为,代入得,、的纵坐标分别为。 ,于是半径,而该圆恰好过双曲线的右顶点, 。即,就是,整理为,解得。
15.答案:
解: , 当时,,此时,切点为,切线方程为,即。
16.答案:B
解:按导函数(为二次函数)的符号及三次函数的单调性可知图①与②正确,图③与④错误。
三、解答题:本大题共74分,解答应写出文字说明,证明过程或演算步骤。
17.解:①(先寻找必要条件)若且,则且,得,而,。
②(再证明上面所求得的必要条件又是充分条件)若,则、,从而=,得。
故当、为实数时,使且成立的充要条件为。
18.解: 四个顶点为, ;
四个焦点为, 。
=(当且仅当时“=”号成立)。
故的最大值为。
19.解:设铁盒的容积为V,则
,由及,得。令,得(舍去)或。 时,;而时,。时,。
20.解: , ,即椭圆方程为,
设、,由得
,,于是,
,
,即,得,解得。故所求椭圆方程为。
21.解:建系如图,设,,其中
为双曲线的半焦距,是梯形的高。
由定比分点坐标公式得,
设双曲线方程为,则离心率。
将C、E的坐标和代入双曲线方程得,
① ②
由①得,代入②并整理得,。故为所求双曲线的离心率。
22.解:求得,
极大值为1,极小值为-1,
(*)有二根,且。 ①
又,即 ②,
,即 ③
②+③得 ④
①入④并整理得, 。 =0。
将代入(*)得,而, ,代入②得=2。
故=2,=0为所求。
O
O
O
O
②
③
④
E
D
C
B
A
E
D
C
B
A
O
