7.5 多边形的内角和与外角和-2021春苏科版七年级数学下册课件(共31张PPT)
文档属性
| 名称 | 7.5 多边形的内角和与外角和-2021春苏科版七年级数学下册课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 694.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览










文档简介
第七章 平面图形的认识(二)
二、多边形的内角和
与外角和
教学新知
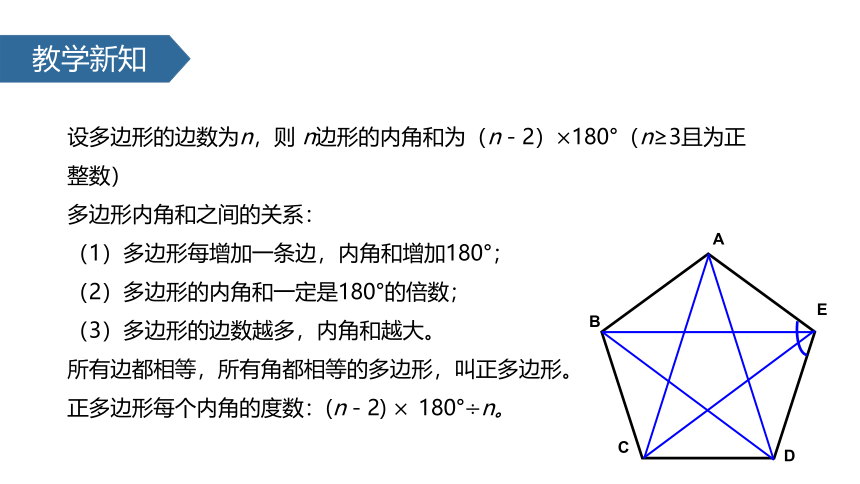
设多边形的边数为n,则 n边形的内角和为(n-2)×180°(n≥3且为正整数)
多边形内角和之间的关系:
(1)多边形每增加一条边,内角和增加180°;
(2)多边形的内角和一定是180°的倍数;
(3)多边形的边数越多,内角和越大。
所有边都相等,所有角都相等的多边形,叫正多边形。
正多边形每个内角的度数:(n-2) ×?180°÷n。
?
D
B
A
E
C
知识要点
2.通过将多边形分割成三角形,探索出多边形内角和的计算公式,能运用相关结论进行有关的推理和计算。
1.理解多边形内角和的推导方法 ,会用多边形内角和公式求多边形的内角和。
知识梳理
知识点1:三角形的内角和.
【例】△ABC中,∠A: ∠B: ∠C=1:2:3,试判断△ABC的形状,并说明理由.
【讲解】引用辅助量x,用x表示出△ABC的三个内角,在△ABC中,运用三角形内角和性质构造方程,解方程后,求出△ABC中最的大角∠C=90°,从而判断△ABC的形状.
答案:△ABC是直角三角形.
理由:∵∠A: ∠B: ∠C=1:2:3,
∴可设∠A、∠B、∠C的度数分别为x°、(2x)°、(3x)°
知识梳理
在△ABC中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°)
∴x+2x+3x=180
解之得:x=30
∴∠C=(3x)°=90°
∴△ABC是直角三角形.
【方法小结】在明确三角形的三个内角关系的条件下,求三角形的内角时,常用方程思想,即运用“三角形三个内角的和等于180°”作为相等关系列方程来求角.
知识梳理
知识点:多边形的内角和
【例】小美在计算一个多边形内角和时,漏算了一个内角,其余各内角之和为1680°那么除去的这个内角的度数为 .
120°
【讲解】∵1680°÷180°=9…60°,又120°+60°=180°∴这个内角度数为120°.
【方法小结】多边形的内角和是180°的整数倍,因此考虑用除法求得多余或者缺少的角的度数.
知识梳理
【小练习】
1. 已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
B
知识梳理
2.如果一个多边形的边数增加1倍,它的内角和是2160°,求原来多边形的边数.
3.小丽同学在进行多边形的内角和计算时,求得内角和为1125°.?当她发现错了之后,重新检查,发现少算了一个内角,你能求出这个内角是多少度,她求的是多少边形的内角和?
【参考答案】七边形。
【参考答案】九边形。
知识梳理
知识点:多边形的外角及外角和
【例】已知一个多边形的内角和比外角和多360°,求这个多边形的边数.
【讲解】任意多边形的外角和都等于360°,则这个多边形的内角和等于360°
+360°,利用方程思想可求出多边形的边数.
【解】设这个多边形的边数为n,则它的内角和是(n-2)·180°,因为任意多边形的外角和是360°,所以得(n-2)·180°=360°+360°.解得n=6.所以,这个多边形的边数是6.
知识梳理
【小练习】
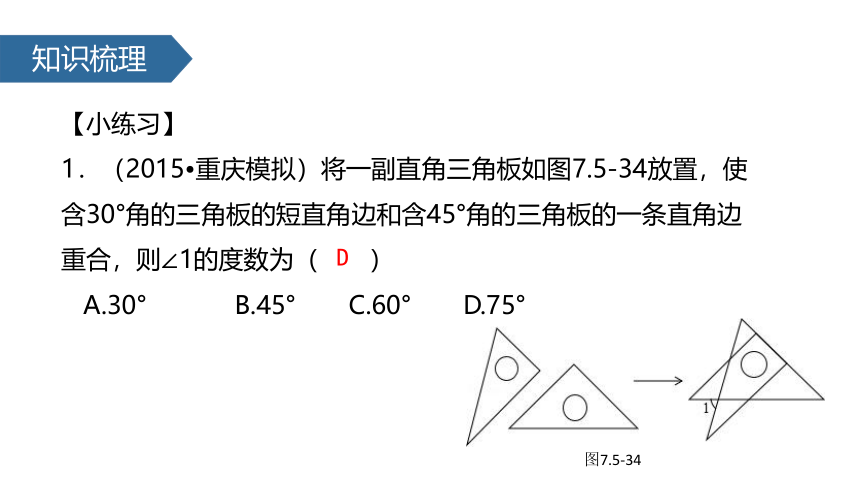
1.(2015?重庆模拟)将一副直角三角板如图7.5-34放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
D
图7.5-34
A.30° B.45° C.60° D.75°
知识梳理
2. 三角形三个外角比为3∶4∶5,则三个内角比为__________。
3. (2012江苏南京中考)如图7.5-35,∠1 、 ∠2 、 ∠3 、 ∠4 是五边形ABCDE的4个外角,若∠A=120° ,则∠1 + ∠2 +∠3 + ∠4= ____________。
?
3∶2∶1
300°
图7.5-35
知识梳理
4.一个多边形的内角和与外角和的和为2520°,求这个多边形的边数.
【参考答案】14边形.
中考在线
考点: 三角形内角和性质.
【例】(2014江苏镇江)如图7.5-5,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=_______°.
图7.5-5
45°
【讲解】垂线带来直角三角形,三角形三个内角的和等于180°,平行线带来相等的角(或互补的角)等等,这是根据已知角求未知角之类的问题要能够发现的信息.
中考在线
1.(2015四川省绵阳)如图7.5-7,在△ABC中,∠B、∠C的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC= ( ).
A.118° B.119° C.120° D.121°
C
图7.5-7
2.(2014湖北襄阳)如图7.5-8,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
A.35° B.45° C.55° D.65°
A
图7.5-8
中考在线
3.(2014湖南益阳)如图7.5-9,EF∥BC,AC平分∠BAF,∠B=
80°.求∠C的度数.
图7.5-9
【参考答案】解法一:∵EF∥BC, ∴∠BAF=180°-∠B=100°.
∵AC平分∠BAF, ∴∠CAF=12∠BAF=50°,∵EF∥BC,∴∠C=∠CAF=50°.
解法二:∵EF∥BC, ∴∠BAF=180°-∠B=100°.∵AC平分∠BAF, ∴∠BAC=12∠BAF=50°,
∵∠C+∠B+∠BAC=180°,∴∠C=180°-(80°+50°)=50°。
?
中考在线
考点:多边形的内角和.
【例】(2014山东莱芜)若一个正多边形的每个内角为156°,则这个正多边形的边数是( )
A. 13 B. 14 C. 15 D. 16
【讲解】正多边形的内角和为: °,每个内角都相等,直接代入公式,得15. 选C.
【方法小结】掌握多边形的内角和公式.直接代入.
C
中考在线
中考在线
1. (2015浙江省丽水)一个多边形的每个内角均为120°,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D七边形
2. (2014?毕节地区)如图7.5-22,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
B
C
知识梳理
图7.5-22
A.13 B.14 C.15 D.16
3.(2014福建厦门)四边形的内角和是 .
360°
知识梳理
4. (2014 巴中)若一个正多边形的一个内角等于135°,那么这个多边形是正 边形.
八
中考在线
考点: 多边形的外角和
【例】(2014?抚顺)将正三角形、正四边形、正五边形按如图7.5-36所示的位置摆放.如果∠3=32°,那么∠1+∠2= 度.
70°
知识梳理
图7.5-36
图7.5-37
知识梳理
【讲解】 如图7.5-37,∵∠3=32°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,
∴∠4=180°﹣60°﹣32°=88°,
∴∠5+∠6=180°﹣88°=92°,
∴∠5=180°﹣∠2﹣108° ①,
∠6=180°﹣90°﹣∠1=90°﹣∠1 ②,
∴①+②得,180°﹣∠2﹣108°+90°﹣∠1=92°,即∠1+∠2=70°.
故答案为:70°.
知识梳理
【方法小结】分别根据正三角形、正四边形、正五边形各内角的度数及平角的定义进行解答即可.熟知正三角形、正四边形、正五边形各内角的度数是解答此类题的关键.
【实战演练】
(2014?昆明)如图7.5-38,在△ABC中,∠A=50°,∠ABC
=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
A
知识梳理
图7.5-38
2.(2015贵州省铜仁)如果一个多边形的每一个外角都是60°,则这个多边形的个数是( )
A.3 B.4 C.5 D.6
D
图7.5-11
课堂练习
1. 在△ABC中,已知∠A=2∠B,∠C=3∠B,则三角形△ABC是(??? ).
A.锐角三角形? B.直角三角形? C.钝角三角形 ???D.形状无法确定
2. 如图7.5-11,与∠ACE互余的角的个数有(??? ).
A.1个 ? ?B.2个 ??? C.3个 ??? D.4个
B
C
课堂练习
3.若n边形的内角和是1260°,则边数n为( ).
A.8 B.9 C.10 D.11
4. 一个多边形的每一个内角都是144°,则此多边形的边数为( ).
A.8 B.10 C.12 D.14
B
B
1. 在凸10边形的所有内角中,锐角的最多个数是( )
A.0 B.1 C.3 D.5
C
课堂练习
5. 一个正多边形它的一个外角等于与它不相邻的内角的13,则这个多边形是( )
A.正十二边形 B.正十边形 C.正八边形 D.正六边形
?
C
6. 若一个直角三角形的一锐角为20°,则另一锐角为______.
70°
课堂练习
图7.5-24
7.(2013?乐山)如图7.5-24,在四边形ABCD中,∠A=45°.直线?与边AB,AD分别相交于点M,N,则∠1+∠2= .
?
225°
图7.5-14
课后习题
1. 已知△ABC中,∠B是∠A的2倍, ∠C比∠A大20° ,则∠A等于( )
A. 40° B. 60° C. 80° D. 90°
2. 如图7.5-14,三角形被遮住的两个角不可能是 ( )
A.一个锐角,一个钝角 B.两个锐角 C.一个锐角,一个直角D.两个钝角
A
D
课后习题
3. 一个三角形的3个内角中,最多能有_______个直角;最多能有_______个钝角;最少有_______个锐角( ).
A.1,1,1 B.1,2,1 C.2,1,1 D.2,2,2
4. 某多边形的内角和是其四边形内角和的3倍,则此多边形的边数是( ).
A.5 B.6 C.7 D.8
B
D
课后习题
5. (2014?来宾)如果一个多边形的内角和是720°,那么这个多边形是( )
A. 四边形 B.五边形 C.六边形 D.七边形
6.如图7.5-26,一块四边形绿化园地,四角都做有半径为2m的圆形喷水池,则这四个喷水池占去的绿化园地的面积为( )
A.4π B.2π C.π D.无法确定
A
C
二、多边形的内角和
与外角和
教学新知
设多边形的边数为n,则 n边形的内角和为(n-2)×180°(n≥3且为正整数)
多边形内角和之间的关系:
(1)多边形每增加一条边,内角和增加180°;
(2)多边形的内角和一定是180°的倍数;
(3)多边形的边数越多,内角和越大。
所有边都相等,所有角都相等的多边形,叫正多边形。
正多边形每个内角的度数:(n-2) ×?180°÷n。
?
D
B
A
E
C
知识要点
2.通过将多边形分割成三角形,探索出多边形内角和的计算公式,能运用相关结论进行有关的推理和计算。
1.理解多边形内角和的推导方法 ,会用多边形内角和公式求多边形的内角和。
知识梳理
知识点1:三角形的内角和.
【例】△ABC中,∠A: ∠B: ∠C=1:2:3,试判断△ABC的形状,并说明理由.
【讲解】引用辅助量x,用x表示出△ABC的三个内角,在△ABC中,运用三角形内角和性质构造方程,解方程后,求出△ABC中最的大角∠C=90°,从而判断△ABC的形状.
答案:△ABC是直角三角形.
理由:∵∠A: ∠B: ∠C=1:2:3,
∴可设∠A、∠B、∠C的度数分别为x°、(2x)°、(3x)°
知识梳理
在△ABC中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°)
∴x+2x+3x=180
解之得:x=30
∴∠C=(3x)°=90°
∴△ABC是直角三角形.
【方法小结】在明确三角形的三个内角关系的条件下,求三角形的内角时,常用方程思想,即运用“三角形三个内角的和等于180°”作为相等关系列方程来求角.
知识梳理
知识点:多边形的内角和
【例】小美在计算一个多边形内角和时,漏算了一个内角,其余各内角之和为1680°那么除去的这个内角的度数为 .
120°
【讲解】∵1680°÷180°=9…60°,又120°+60°=180°∴这个内角度数为120°.
【方法小结】多边形的内角和是180°的整数倍,因此考虑用除法求得多余或者缺少的角的度数.
知识梳理
【小练习】
1. 已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
B
知识梳理
2.如果一个多边形的边数增加1倍,它的内角和是2160°,求原来多边形的边数.
3.小丽同学在进行多边形的内角和计算时,求得内角和为1125°.?当她发现错了之后,重新检查,发现少算了一个内角,你能求出这个内角是多少度,她求的是多少边形的内角和?
【参考答案】七边形。
【参考答案】九边形。
知识梳理
知识点:多边形的外角及外角和
【例】已知一个多边形的内角和比外角和多360°,求这个多边形的边数.
【讲解】任意多边形的外角和都等于360°,则这个多边形的内角和等于360°
+360°,利用方程思想可求出多边形的边数.
【解】设这个多边形的边数为n,则它的内角和是(n-2)·180°,因为任意多边形的外角和是360°,所以得(n-2)·180°=360°+360°.解得n=6.所以,这个多边形的边数是6.
知识梳理
【小练习】
1.(2015?重庆模拟)将一副直角三角板如图7.5-34放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
D
图7.5-34
A.30° B.45° C.60° D.75°
知识梳理
2. 三角形三个外角比为3∶4∶5,则三个内角比为__________。
3. (2012江苏南京中考)如图7.5-35,∠1 、 ∠2 、 ∠3 、 ∠4 是五边形ABCDE的4个外角,若∠A=120° ,则∠1 + ∠2 +∠3 + ∠4= ____________。
?
3∶2∶1
300°
图7.5-35
知识梳理
4.一个多边形的内角和与外角和的和为2520°,求这个多边形的边数.
【参考答案】14边形.
中考在线
考点: 三角形内角和性质.
【例】(2014江苏镇江)如图7.5-5,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=_______°.
图7.5-5
45°
【讲解】垂线带来直角三角形,三角形三个内角的和等于180°,平行线带来相等的角(或互补的角)等等,这是根据已知角求未知角之类的问题要能够发现的信息.
中考在线
1.(2015四川省绵阳)如图7.5-7,在△ABC中,∠B、∠C的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC= ( ).
A.118° B.119° C.120° D.121°
C
图7.5-7
2.(2014湖北襄阳)如图7.5-8,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
A.35° B.45° C.55° D.65°
A
图7.5-8
中考在线
3.(2014湖南益阳)如图7.5-9,EF∥BC,AC平分∠BAF,∠B=
80°.求∠C的度数.
图7.5-9
【参考答案】解法一:∵EF∥BC, ∴∠BAF=180°-∠B=100°.
∵AC平分∠BAF, ∴∠CAF=12∠BAF=50°,∵EF∥BC,∴∠C=∠CAF=50°.
解法二:∵EF∥BC, ∴∠BAF=180°-∠B=100°.∵AC平分∠BAF, ∴∠BAC=12∠BAF=50°,
∵∠C+∠B+∠BAC=180°,∴∠C=180°-(80°+50°)=50°。
?
中考在线
考点:多边形的内角和.
【例】(2014山东莱芜)若一个正多边形的每个内角为156°,则这个正多边形的边数是( )
A. 13 B. 14 C. 15 D. 16
【讲解】正多边形的内角和为: °,每个内角都相等,直接代入公式,得15. 选C.
【方法小结】掌握多边形的内角和公式.直接代入.
C
中考在线
中考在线
1. (2015浙江省丽水)一个多边形的每个内角均为120°,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D七边形
2. (2014?毕节地区)如图7.5-22,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
B
C
知识梳理
图7.5-22
A.13 B.14 C.15 D.16
3.(2014福建厦门)四边形的内角和是 .
360°
知识梳理
4. (2014 巴中)若一个正多边形的一个内角等于135°,那么这个多边形是正 边形.
八
中考在线
考点: 多边形的外角和
【例】(2014?抚顺)将正三角形、正四边形、正五边形按如图7.5-36所示的位置摆放.如果∠3=32°,那么∠1+∠2= 度.
70°
知识梳理
图7.5-36
图7.5-37
知识梳理
【讲解】 如图7.5-37,∵∠3=32°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,
∴∠4=180°﹣60°﹣32°=88°,
∴∠5+∠6=180°﹣88°=92°,
∴∠5=180°﹣∠2﹣108° ①,
∠6=180°﹣90°﹣∠1=90°﹣∠1 ②,
∴①+②得,180°﹣∠2﹣108°+90°﹣∠1=92°,即∠1+∠2=70°.
故答案为:70°.
知识梳理
【方法小结】分别根据正三角形、正四边形、正五边形各内角的度数及平角的定义进行解答即可.熟知正三角形、正四边形、正五边形各内角的度数是解答此类题的关键.
【实战演练】
(2014?昆明)如图7.5-38,在△ABC中,∠A=50°,∠ABC
=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
A
知识梳理
图7.5-38
2.(2015贵州省铜仁)如果一个多边形的每一个外角都是60°,则这个多边形的个数是( )
A.3 B.4 C.5 D.6
D
图7.5-11
课堂练习
1. 在△ABC中,已知∠A=2∠B,∠C=3∠B,则三角形△ABC是(??? ).
A.锐角三角形? B.直角三角形? C.钝角三角形 ???D.形状无法确定
2. 如图7.5-11,与∠ACE互余的角的个数有(??? ).
A.1个 ? ?B.2个 ??? C.3个 ??? D.4个
B
C
课堂练习
3.若n边形的内角和是1260°,则边数n为( ).
A.8 B.9 C.10 D.11
4. 一个多边形的每一个内角都是144°,则此多边形的边数为( ).
A.8 B.10 C.12 D.14
B
B
1. 在凸10边形的所有内角中,锐角的最多个数是( )
A.0 B.1 C.3 D.5
C
课堂练习
5. 一个正多边形它的一个外角等于与它不相邻的内角的13,则这个多边形是( )
A.正十二边形 B.正十边形 C.正八边形 D.正六边形
?
C
6. 若一个直角三角形的一锐角为20°,则另一锐角为______.
70°
课堂练习
图7.5-24
7.(2013?乐山)如图7.5-24,在四边形ABCD中,∠A=45°.直线?与边AB,AD分别相交于点M,N,则∠1+∠2= .
?
225°
图7.5-14
课后习题
1. 已知△ABC中,∠B是∠A的2倍, ∠C比∠A大20° ,则∠A等于( )
A. 40° B. 60° C. 80° D. 90°
2. 如图7.5-14,三角形被遮住的两个角不可能是 ( )
A.一个锐角,一个钝角 B.两个锐角 C.一个锐角,一个直角D.两个钝角
A
D
课后习题
3. 一个三角形的3个内角中,最多能有_______个直角;最多能有_______个钝角;最少有_______个锐角( ).
A.1,1,1 B.1,2,1 C.2,1,1 D.2,2,2
4. 某多边形的内角和是其四边形内角和的3倍,则此多边形的边数是( ).
A.5 B.6 C.7 D.8
B
D
课后习题
5. (2014?来宾)如果一个多边形的内角和是720°,那么这个多边形是( )
A. 四边形 B.五边形 C.六边形 D.七边形
6.如图7.5-26,一块四边形绿化园地,四角都做有半径为2m的圆形喷水池,则这四个喷水池占去的绿化园地的面积为( )
A.4π B.2π C.π D.无法确定
A
C
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
