9.1 乘法公式-2021春苏科版七年级数学下册课件(共22张PPT)
文档属性
| 名称 | 9.1 乘法公式-2021春苏科版七年级数学下册课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 571.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览









文档简介
第九章 整式乘法与因式分解
一、乘法公式
教学新知
完全平方公式:
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
平方差公式:
a2-b2= (a+b)(a-b) .
知识要点
2.会推导平方差公式,并能正确运用公式进行计算。
1.会推导完全平方公式,并能正确运用公式进行计算。
3.培养学生主动探索、敢于实践、勇于发现的科学精神似及合作交流的能力和创新意识。
知识梳理
知识点梳理
知识点:完全平方公式.
【例】计算:(-2x+5y)2
【讲解】若运用完全平方公式:(a+b)2=a2+2ab+b2则可以把-2x看作是a,把5y看作是b,若运用完全平方公式:(a-b)2=a2-2ab+b2,首先,把两个加数交换位置,即:(5y-2x)2则可以把5y看作是a,把2x看作是b,
解1:原式=(-2x)2+2(-2x)(5y)+(5y)2=4 x2-20xy+25 y2.
解2:原式=(5y-2x)2=(5y)2-2×5y×2x+(2x)2=4 x2-20xy+25 y2.
知识梳理
【方法小结】根据完全平方公式(a-b)2=a2-2ab+b2展开即可,公式中的a、b所表示的可以是数、单项式、多项式.
【小练习】
下列计算中正确的是( )
A
B
C
D
C
知识梳理
2. 有若干张面积分别为纸片,阳阳从中抽取了1张面积为a2的正方形纸片,4张面积为ab的长方形纸片,若他想拼成一个大正方形,则还需要抽取面积为b2的正方形纸片( )
A.2张 B.4张 C.6张 D.8张
3. 计算:(1)(-2a+12b)2; (2)(-4b-23)2
?
4.用简便方法计算: 1982.
参考答案:(1)4a2-2ab+14b2;(2)14b2+43b+49
?
参考答案:原式=(200-2)2=2002-2×200×2+22=39204.
B
知识梳理
知识点:平方差公式
【例】计算:(3mn-2)(-3mn-2).
【讲解】可先转化为(3mn-2)(-3mn-2)=(-2+3mn)(-2-3mn)再用平方差公式计算.
【解】 (3mn-2)(-3mn-2)=(-2+3mn)(-2-3mn)=(-2)2-(3mn)2=4-9m2n2.
【方法小结】能用平方差公式计算的两个二项式相乘必须满足:有一项完全相同,另一项互为相反数.注意把相同的项作为a,相反的项作为b.
知识梳理
【小练习】
1. 下列能用平方差公式计算的是( )
A.(x+y)(-x-y) B.(-a+b)(a-b)
C.(-a-b)(-a+b) D.(x-y)(x-y)
C
2. 填空:(-x+7)(-x-7)= ,
(3x+5y)? =9x2-25y2.
3. 计算:
(1)(2x+3y)(2x-3y);(2)(-1-2a)(2a-1).
x2-49
3x-5y
知识梳理
参考答案:(1)4x2-9y2;(2)1-4a2
4. 计算(x+1)(x-1)(x2+1)
参考答案:原式=(x2-1)(x2+1)=x4-1
知识点: 乘法公式的综合运算.
【例】(2015湖南长沙)先化简,再求值:
,其中 , 。
知识梳理
【讲解】先利用乘法公式进行整式的乘法运算,再合并同类项.最后求值.
解:原式
当 , 时,原式 。
【方法小结】解题的关键是掌握多项式乘以多项式和整式加减的法则.此类问题容易出错的地方是平方差公式(a+b)(a-b)=a2-b2与完全平方公式(a±b)2=a2±2ab+b2的结构特征分不清,出现张冠李戴现象.
知识梳理
【小练习】
(2014?邵阳 )下列计算正确的是 ( )
A.2x-x=x B. a3?a2 = a6 C. (a-b)2 = a2-b2 D. (a+b)(a-b)=a2+b2
?
2. (2014?临沂)请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+xn)的结果是( )
A.1﹣xn+1 B. 1+xn+1 C. 1﹣xn D. 1+xn
知识梳理
3.(2014?包头)计算:( x+1)2-(x+2)(x-2)= .
4. (2014?厦门)设a=192×918,b=8882-302,c=10532-7472,则数a,b,c 按从小到大的顺序排列,结果是
< < .
5. (2014?宁波)化简:(a+b)2+(a-b)(a+b)-2ab;
【参考答案】1.A 2. A 3.2x+5 4. a c b 5. 原式=a2+2ab+b2+a2﹣b2﹣2ab=2a2.
课堂练习
1. (2014年福建三明)下列计算正确的是( )
A.(a3)2=a5 B.a6÷a3=a2 C.(ab)2=a2b2
D.(a+b)2=a2+b2
2. 图9.4-2的图①是一个边长为(m+n)的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A.(m+n)2﹣(m﹣n)2=4mn B.(m+n)2﹣(m2+n2)=2mn
C.(m﹣n)2+2mn=m2+n2 D.(m+n)(m﹣n)=m2﹣n2
C
B
课堂练习
图9.4-2
3. (_________)(a+b+c)=a2-(b+c)2;
0.09x2-0.6x+_____=(0.3x-_____)2.
a-b-c
1
1
课堂练习
4. a4-(1-a)(1+a)(1+a2)(1+a)= .
2a4+a5﹣a﹣1
5. 计算:
(1)
(2)
(3)
(4)
参考答案:
课堂练习
6. 如图9.4-7,2015个正方形由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2005cm,向里依次为2014cm,2013cm,
…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?
图9.4-7
课堂练习
参考答案:
解:S阴影=(20152-20142)+(20132-20122)+…+(32-22)+1=2015+2014+…+3+2+1=2031120 cm2.答:所有阴影部分的面积和是2031120cm2.
课后习题
1. 下列各式中,计算结果是 的是( )
A.
B.
C.
D.
2. 利用图形中面积的等量关系可以得到某些数学公式.例如,根据图9.4-3的甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
B
B
A.(a+b)(a﹣b)=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2
C.a(a+b)=a2+ab D.a(a﹣b)=a2﹣ab
课后习题
图9.4-3
3. ( -4b)( + 4b)=9a2-16b2.
4. 98×102=( )( )=(?? )2-(? )2=_______.
3a
3a
100-2
100+2
100
2
9996
课后习题
5. 计算:
(1)(2x-3y)2
(2)
(3)
(1)
(2)
(3)
参考答案:
6. 设m+n=10,mn=24,求(1)m2+n2;(2)(m-n)2的值。
课后习题
参考答案:
∵m+n=10,mn=24,且m2+n2=(m+n)2-2mn,(m-n)2=(m+n)2-4mn,将m+n
=10,mn=24分别代入上面两式可得m2+n2=102-2×24=52,(m-n)2=100-4×24=4
?
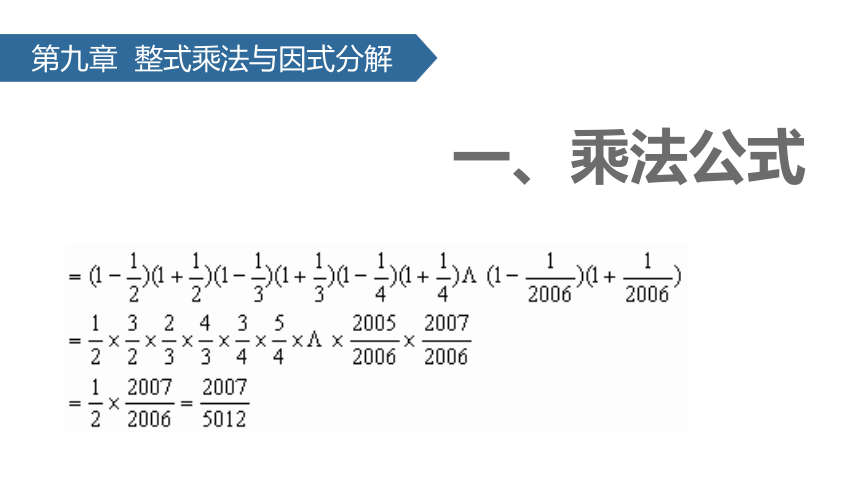
7. 阅读下列材料:一个自然数a恰好等于另一个自然数b的平方,则称自然数a为完全平方数.已知a=20142+20142×20152+
20152,试说明a是一个完全平方数.
课后习题
参考答案:设x=2014,则2015=2014+1=x+1,故有:
a=x2+x2(x+1)2+(x+1)2,
=x2﹣2x(x+1)+(x+1)2+2x(x+1)+x2(x+1)2,
=[x﹣(x+1)]2+2x(x+1)+x2(x+1)2,
=1+2x(x+1)+x2(x+1)2,
=[1+x(x+1)]2,
=[1+x+x2]2,
=(1+2014+20142)2,
∴a是一个完全平方数.
一、乘法公式
教学新知
完全平方公式:
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
平方差公式:
a2-b2= (a+b)(a-b) .
知识要点
2.会推导平方差公式,并能正确运用公式进行计算。
1.会推导完全平方公式,并能正确运用公式进行计算。
3.培养学生主动探索、敢于实践、勇于发现的科学精神似及合作交流的能力和创新意识。
知识梳理
知识点梳理
知识点:完全平方公式.
【例】计算:(-2x+5y)2
【讲解】若运用完全平方公式:(a+b)2=a2+2ab+b2则可以把-2x看作是a,把5y看作是b,若运用完全平方公式:(a-b)2=a2-2ab+b2,首先,把两个加数交换位置,即:(5y-2x)2则可以把5y看作是a,把2x看作是b,
解1:原式=(-2x)2+2(-2x)(5y)+(5y)2=4 x2-20xy+25 y2.
解2:原式=(5y-2x)2=(5y)2-2×5y×2x+(2x)2=4 x2-20xy+25 y2.
知识梳理
【方法小结】根据完全平方公式(a-b)2=a2-2ab+b2展开即可,公式中的a、b所表示的可以是数、单项式、多项式.
【小练习】
下列计算中正确的是( )
A
B
C
D
C
知识梳理
2. 有若干张面积分别为纸片,阳阳从中抽取了1张面积为a2的正方形纸片,4张面积为ab的长方形纸片,若他想拼成一个大正方形,则还需要抽取面积为b2的正方形纸片( )
A.2张 B.4张 C.6张 D.8张
3. 计算:(1)(-2a+12b)2; (2)(-4b-23)2
?
4.用简便方法计算: 1982.
参考答案:(1)4a2-2ab+14b2;(2)14b2+43b+49
?
参考答案:原式=(200-2)2=2002-2×200×2+22=39204.
B
知识梳理
知识点:平方差公式
【例】计算:(3mn-2)(-3mn-2).
【讲解】可先转化为(3mn-2)(-3mn-2)=(-2+3mn)(-2-3mn)再用平方差公式计算.
【解】 (3mn-2)(-3mn-2)=(-2+3mn)(-2-3mn)=(-2)2-(3mn)2=4-9m2n2.
【方法小结】能用平方差公式计算的两个二项式相乘必须满足:有一项完全相同,另一项互为相反数.注意把相同的项作为a,相反的项作为b.
知识梳理
【小练习】
1. 下列能用平方差公式计算的是( )
A.(x+y)(-x-y) B.(-a+b)(a-b)
C.(-a-b)(-a+b) D.(x-y)(x-y)
C
2. 填空:(-x+7)(-x-7)= ,
(3x+5y)? =9x2-25y2.
3. 计算:
(1)(2x+3y)(2x-3y);(2)(-1-2a)(2a-1).
x2-49
3x-5y
知识梳理
参考答案:(1)4x2-9y2;(2)1-4a2
4. 计算(x+1)(x-1)(x2+1)
参考答案:原式=(x2-1)(x2+1)=x4-1
知识点: 乘法公式的综合运算.
【例】(2015湖南长沙)先化简,再求值:
,其中 , 。
知识梳理
【讲解】先利用乘法公式进行整式的乘法运算,再合并同类项.最后求值.
解:原式
当 , 时,原式 。
【方法小结】解题的关键是掌握多项式乘以多项式和整式加减的法则.此类问题容易出错的地方是平方差公式(a+b)(a-b)=a2-b2与完全平方公式(a±b)2=a2±2ab+b2的结构特征分不清,出现张冠李戴现象.
知识梳理
【小练习】
(2014?邵阳 )下列计算正确的是 ( )
A.2x-x=x B. a3?a2 = a6 C. (a-b)2 = a2-b2 D. (a+b)(a-b)=a2+b2
?
2. (2014?临沂)请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+xn)的结果是( )
A.1﹣xn+1 B. 1+xn+1 C. 1﹣xn D. 1+xn
知识梳理
3.(2014?包头)计算:( x+1)2-(x+2)(x-2)= .
4. (2014?厦门)设a=192×918,b=8882-302,c=10532-7472,则数a,b,c 按从小到大的顺序排列,结果是
< < .
5. (2014?宁波)化简:(a+b)2+(a-b)(a+b)-2ab;
【参考答案】1.A 2. A 3.2x+5 4. a c b 5. 原式=a2+2ab+b2+a2﹣b2﹣2ab=2a2.
课堂练习
1. (2014年福建三明)下列计算正确的是( )
A.(a3)2=a5 B.a6÷a3=a2 C.(ab)2=a2b2
D.(a+b)2=a2+b2
2. 图9.4-2的图①是一个边长为(m+n)的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A.(m+n)2﹣(m﹣n)2=4mn B.(m+n)2﹣(m2+n2)=2mn
C.(m﹣n)2+2mn=m2+n2 D.(m+n)(m﹣n)=m2﹣n2
C
B
课堂练习
图9.4-2
3. (_________)(a+b+c)=a2-(b+c)2;
0.09x2-0.6x+_____=(0.3x-_____)2.
a-b-c
1
1
课堂练习
4. a4-(1-a)(1+a)(1+a2)(1+a)= .
2a4+a5﹣a﹣1
5. 计算:
(1)
(2)
(3)
(4)
参考答案:
课堂练习
6. 如图9.4-7,2015个正方形由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2005cm,向里依次为2014cm,2013cm,
…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?
图9.4-7
课堂练习
参考答案:
解:S阴影=(20152-20142)+(20132-20122)+…+(32-22)+1=2015+2014+…+3+2+1=2031120 cm2.答:所有阴影部分的面积和是2031120cm2.
课后习题
1. 下列各式中,计算结果是 的是( )
A.
B.
C.
D.
2. 利用图形中面积的等量关系可以得到某些数学公式.例如,根据图9.4-3的甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
B
B
A.(a+b)(a﹣b)=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2
C.a(a+b)=a2+ab D.a(a﹣b)=a2﹣ab
课后习题
图9.4-3
3. ( -4b)( + 4b)=9a2-16b2.
4. 98×102=( )( )=(?? )2-(? )2=_______.
3a
3a
100-2
100+2
100
2
9996
课后习题
5. 计算:
(1)(2x-3y)2
(2)
(3)
(1)
(2)
(3)
参考答案:
6. 设m+n=10,mn=24,求(1)m2+n2;(2)(m-n)2的值。
课后习题
参考答案:
∵m+n=10,mn=24,且m2+n2=(m+n)2-2mn,(m-n)2=(m+n)2-4mn,将m+n
=10,mn=24分别代入上面两式可得m2+n2=102-2×24=52,(m-n)2=100-4×24=4
?
7. 阅读下列材料:一个自然数a恰好等于另一个自然数b的平方,则称自然数a为完全平方数.已知a=20142+20142×20152+
20152,试说明a是一个完全平方数.
课后习题
参考答案:设x=2014,则2015=2014+1=x+1,故有:
a=x2+x2(x+1)2+(x+1)2,
=x2﹣2x(x+1)+(x+1)2+2x(x+1)+x2(x+1)2,
=[x﹣(x+1)]2+2x(x+1)+x2(x+1)2,
=1+2x(x+1)+x2(x+1)2,
=[1+x(x+1)]2,
=[1+x+x2]2,
=(1+2014+20142)2,
∴a是一个完全平方数.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
