12.1 证明-2021春苏科版七年级数学下册课件(共47张PPT)
文档属性
| 名称 | 12.1 证明-2021春苏科版七年级数学下册课件(共47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 13:44:12 | ||
图片预览











文档简介
第十二章 证明
12.1 证明
教学新知
证明:根据已知的真命题,确定某个命题真实性的过程叫做证明.
定理:经过证明的真命题称为定理.
1.经历探索些问题时,由于“直观判断不可靠”、“直观无法做出确定判断”,但运用已有的数学知识和方法可以确定个数学结论的正确性的过程,举反例说明结论的错误性,初步感受说理的必要性.。
知识要点
2.尝试用说理的方法解决问题,在交流中发展有条理思考和有条理表达的能力。
图12.2-8
知识梳理
知识点梳理
知识点:事件的判断.
【例】如图12.2-8,假如用一根比地球赤道长1m的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大(把地球看作球形)?能伸进一根小手指吗?能放进一只拳头吗?
知识梳理
【讲解】解:设地球赤道的周长为c,半径为R1 ,铁丝的半径为R2,
则R2?R1=????+12?????????2????=12????≈0.16(m)
显然,这样的间隙不仅可以伸进一根小手指,而且也能放进一只拳头.
?
【方法小结】不能仅凭表面直觉去判断,计算是检验数学结论常用的方法.
【小练习】如图12.2-9,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大一些?
知识梳理
图12.2-9
【参考答案】直觉上判断第二个大圆内的两个小圆的周长之和大一些.我们可以通过计算来证明.设原来大圆的半径为R,则第一个大圆内的每个小圆的半径为????10,则第一个大圆内的十个小圆的周长之和为10×2????× ????10= 2????????;第二个大圆内的两个小圆的周长之和为2×2????× ????2= 2????????;所以它们的周长一样长.
?
知识梳理
知识点梳理
知识点1:证明与定理.
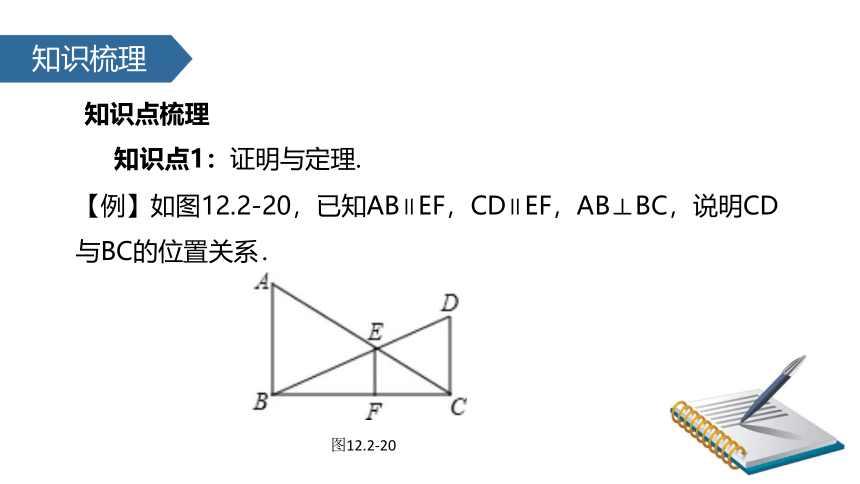
【例】如图12.2-20,已知AB∥EF,CD∥EF,AB⊥BC,说明CD与BC的位置关系.
图12.2-20
知识梳理
【讲解】∵AB∥EF,CD∥EF(已知),
∴AB∥CD,∠ABC+∠BCD=180°(两直线平行,同旁内角互补),
∵AB⊥BC(已知),
∴∠ABC=90°(垂直的定义).
∴∠BCD=180°-90°=90°(等式的性质),
∴CD⊥BC(垂直的定义).
【方法小结】根据已知条件,再结合要证明的,由果索因,综合推理.
【小练习】
知识梳理
1. 在小括号里填写证明理由:已知:如图12.2-21,点A、O、B在一直线上,OM 平分∠AOC,ON平分∠BOC,求证:OM⊥ON.
图12.2-21
知识梳理
证明: ∵OM平分∠AOC( )
∴∠1=12∠AOC( )
∵ON平分∠BOC( )
∴∠2=12∠BOC( )
∴∠1+∠2=12∠AOC+ 12∠BOC=∠MON ( )
∵A、O、B在一直线上( )
?
已知
角平分线定义
已知
角平分线定义
等式性质
已知
知识梳理
∴∠AOB=180°( )
∴∠1+∠2=12 ×180°= 90°( )
∴OM⊥ON( )
?
平角定义
等量代换
垂直定义
2.如图12.2-22:已知BC平分∠ACD,且∠1=∠2,求证:AB∥CD.
图12.2-22
知识梳理
【参考答案】证明:∵BC平分∠ACD(已知),∴∠1=∠BCD(角平分线定义),∵∠1=∠2(已知),∴∠2=∠BCD(等量代换),∴AB∥CD( 内错角相等,两直线平行).
知识点梳理
知识点1:三角形内角和定理的应用.
【例】如图12.2-40,在△ABC中,∠ABC,∠ACB的平分线交于点O,求证:∠BOC=90°??12∠A.
?
知识梳理
【讲解】∵BO,CO分别是∠ABC和∠ACB的平分线(已知),
∴∠ABC=2∠OBC,∠ACB=2∠OCB(角平分线定义),
又在△BOC中,∠BOC+∠OBC+∠OCB=180°(三角形内角和等于180°),
∴∠BOC+12∠ABC+12∠ACB=180°(等量代换),
又∵在△ABC中,∠A+∠ABC+∠ACB=180°(三角形内角和等于180°),
∴∠BOC=12∠A+90°(等式性质).
?
图12.2-40
知识梳理
【方法小结】紧扣三角形内角和等于180°,并能把∠OBC与∠OCB的和视为整体处理.
【小练习】
已知:如图12.2-41,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:∠P=90°.
【参考答案】证明:∵AB∥CD(已知),
∴∠BEF+∠DFE=180°
(两直线平行,同旁内角互补).
图12.2-41
知识梳理
又∵∠BEF的平分线与∠DFE的平分线相交于点P(已知),
∴∠PEF=12∠BEF,∠PFE=12∠DEF
(角平分线定义),
∴∠PEF+∠PFE=12(∠BEF+∠DFE)=90°(等式性质).
∵∠PEF+∠PFE+∠P=180°
(三角形内角和等于180°),
∴∠P=90°(等式性质).
?
图12.2-42
知识梳理
知识点2: 三角形内角和定理的推论
【例】已知:如图12.2-42,AM,CM分别平分∠BAD和∠BCD,
试说明∠M= 12 (∠B+∠D).
?
知识梳理
【讲解】证明:∵AM,CM分别平分∠BAD和∠BCD(已知),
∴∠BAM=∠MAD,∠MCB=∠MCD(角平分线定义),
∵∠ANC=∠B+∠BAM=∠M+∠MCB、
∠AEC=∠MCD+∠D=∠MAD+∠M( 三角形的外角等于和它不相邻的两个内角的和),
∴∠M=∠B+∠BAM-∠MCB①,
∠M=∠MCD+∠D-∠MAD②(等式性质),
∴①+②得:2∠M=∠B+∠D(等式性质),
∴∠M= 12 (∠B+∠D)(等式性质).
?
知识梳理
【方法小结】运用三角形内角和定理的推论来转化。
【小练习】
已知如图12.2-43,在△ABC中,CH是外角∠ACD的平分线,BH是∠ABC的平分线.
求证:∠A=2∠H.
图12.2-43
知识梳理
【参考答案】证明:∵∠ACD是△ABC的一个外角(已知),
∴∠ACD=∠ABC+∠A( 三角形的外角等于和它不相邻的两个内角的和)
∵∠2是△BCD的一个外角(已知),
∴∠2=∠1+∠H( 三角形的外角等于和它不相邻的两个内角的和)
∵CH是外角∠ACD的平分线,BH是∠ABC的平分线(已知)
∴∠1= 12 ∠ABC,∠2= 12 ∠ACD(角平分线性质 )
∴∠A=∠ACD-∠ABC=2(∠2-∠1)(等式的性质)
而∠H=∠2-∠1(等式的性质)
?
知识梳理
中考在线
考点:简单的证明、推理 .
【例】(2015台州)某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是(?? )
A.若甲对,则乙对??? B.若乙对,则甲对? C.若乙错,则甲错??
D.若甲粗,则乙对
D
知识梳理
【讲解】 假设甲说的对,则参加两种比赛的人次大于28,因为共有20位同学,因此两项都参加的人数大于8人次,故乙说的错误;
假设乙说的对,则参加两种比赛的人次小于25,因为共有20位同学,因此只参加一项的人数不大于12人,故甲说法错误;
故选:D.
【方法小结】分两种情况分别进行分析/推理与论证.
【实战演练】
1. (2014河北)如图12.2-44,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是( )。
B
知识梳理
A.20° B.30° C.70° D.80°
2.(2014?永州)小聪,小玲,小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有A、B两个选项,且只有一个选项是正确的,三人的答案和得分如下表,试问:这五道题的正确答案(按1~5题的顺序排列)是_____________________.
BABBA
知识梳理
{5940675A-B579-460E-94D1-54222C63F5DA}题号
答案
选手
1
2
3
4
5
得分
小聪
B
A
A
B
A
40
小玲
B
A
B
A
A
40
小红
A
B
B
B
A
30
3. (2014年湖北随州)将一副直角三角板如图12.2-45放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 度.
75
知识梳理
图12.2-45
4. (2014年福建厦门)A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权,比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队
知识梳理
(有且只有两个队)出线,小组赛结束后,如果A队没有全胜,那么A队的积分至少要几分才能保证一定出线?请说明理由.
[注:单循环比赛就是小组内的每一个队都要和其他队赛一场].
【参考答案】 A队的积分至少要7分才能保证一定出线。
课堂练习
1. 今年五一节期间,王老板在其经营的服装店里卖出两件衣服,其中一件是裤子售价为168元,盈利20%,一件是夹克衫售价也是168元,但亏损20%,问王老板在这次的交易过程中是赚了还是亏了,( ).
A.赚了 B.亏了 C.不赚不亏 D.无法确定
B
2.如图12.2-46,在△ABC中,∠B=67°,∠C=33°,AD是△ABC
的角平分线,则∠CAD的度数为( )
A.40° B.45° C.50° D.55°
A
课堂练习
图12.2-46
3.(2013?泉州)在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
D
课堂练习
4.你认为图12.2-12中,大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大一些?请你猜一猜,并用学过的知识和数学方法验证你的猜想.
图12.2-12
【参考答案】周长相等。
课堂练习
5. 两个连续奇数的平方差能被8整除吗?请说明你的理由.
【参考答案】两个连续奇数的平方差能被8整除.理由:设这两个连续奇数分别为:(2n+1)与(2n-1),∵(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=4n×2=8n.
∴两个连续奇数的平方差能被8整除.
6. 如图12.2-24,若∠3=∠4,你能说明AD∥BC,AB∥DC吗?
小亮回答:都行,∵∠3=∠4,∴AD∥BC,AB∥DC.
课堂练习
图12.2-24
小亮错在哪里,请指出错因,并改正.
【参考答案】1.解:∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),由于没有其它条件不能识别AD∥BC
课堂练习
7.根据提示,同桌合作,完成括号内的依据.
如图12.2-25,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
图12.2-25
课堂练习
证明:BE∥DF.理由如下:
∵∠A=∠C=90°( ),
∴∠ABC+∠ADC=180°( ).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=12∠ABC,∠3=∠4=12∠ADC( ).
∴∠1+∠3=12(∠ABC+∠ADC)=12×180°=90°(等量代换).
又∠1+∠AEB=90°(三角形的内角和等于180°),
?
已知
四边形的内角和等于360°
角平分线的定义
课堂练习
∴∠3=∠AEB(等量代换).
∴ (同位角相等,两直线平行).
BE∥DF
8. 如图12.2-49,已知AB∥CD,求证:∠B+∠D=∠BED.
图12.2-49
课堂练习
【参考答案】(方法不惟一)如图12.2-50, 过E点作EF∥AB,(已作),∴∠1=∠B,(两直线平行,内错角相等),又∵AB∥CD,(已知),∴EF∥CD,∴∠2=∠D,∴∠B+∠D=∠1+∠2,∴∠BED=∠B+∠D.(等量代换)
图12.2-50
课后习题
1. 图12.2-13中,有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心0按逆时针方向进行旋转,每次均旋转45.,第1次旋转后得到图(1),第2次旋转后得到图(2),…,则第10次旋转后得到的图形与图(1)~(4)中相同的是( ).
图12.2-13
B
课后习题
2.对于图12.2-27中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180°
图12.2-27
D
课后习题
3. (2012?长春)如图12.2-51,在Rt△ABC中,∠C=90°.D为边CA延长线上一点,DE∥AB,∠ADE=42°,则∠B的大小为( )
图12.2-51
A.42° B.45° C.48° D.58°
C
课后习题
4. 观察后测量图12.2-14中a,b,c,d四条直线, 。
图12.2-14
a ∥ c
课后习题
5. 如图12.2-28,AB∥CD,∠B=∠C,求证:AC∥BD.
图12.2-28
证明:∵AB∥CD( ),
∴∠A+∠C=180°( ),
已知
两直线平行,同旁内角互补
课后习题
又∵∠B=∠C( ),
∴∠A+∠B=180°( ),
∴AC∥BD( ).
已知
等量代换
同旁内角互补,两直线平行
6.如图12.2-31,AB∥CD,直线MN分别叫AB,CD于点E、F.EG平分∠AEF,EG⊥FG于点G,若∠BEM=50°,则∠CFG= °.
图12.2-31
65
课后习题
7.如图12.2-53,∠1是Rt△ABC的一个外角,直线DE∥BC,分别交边AB、AC于点D、E,∠1=120°,则∠2的度数是 .
图12.2-53
30°
课后习题
8. 若一个正整数能表示为两个连续偶数的平方差,那么这个正整数为“神秘数”.如4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数
(1)28和76是神秘数吗?为什么?
(2)设两个连续偶数为2k+2和2k(k为非负整数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?
课后习题
【参考答案】 (1)是,∵28=82-62,76=202-182.(2)是,∵(2k+2)2-(2k)2=8k+4=4(2k+1),
∴由这两个连续偶数构成的神秘数是4的倍数
9. 如图12.2-17,请你观察,黑白方格间的横线平行吗?先猜想,然后利用合适的方法验证你的猜想.
图12.2-17
课后习题
【参考答案】通过观察黑白方格间的横线不平行,用三角板和直尺验证后发现他们是平行的.
10. 已知:如图12.2-32,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.求证:AB∥CD.
【参考答案】证明:∵GH⊥CD(已知)∴∠CHG=90°(垂直定义).又∵∠2=30°(已知),∴∠3=60°.∴∠4=60°(对顶角相等).又∵∠1=60°(已知),∴∠1=∠4.∴AB∥CD(同位角相等,两直线平行)
课后习题
图12.2-32
11. 已知,如图12.2-55,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.求证:∠DAE=12(∠B-∠C)
?
课后习题
图12.2-55
【参考答案】由图知,∵∠BAC+∠B+∠C =180°(三角形内角和等于180°),∴∠BAC=180°-∠B-∠C(等式性质),∵AD是BC边上的高(已知),∴∠ADB=90°(三角形高的定义),∵∠BAD+∠B+∠ADB=180°(三角形内角和等于180°),∴∠BAD=180°-∠B-∠ADB=90°-∠B(等
课后习题
式性质),∵AE平分∠BAC(已知),∴∠BAE=12∠BAC(角平分线定义),∵∠DAE=∠BAE-∠BAD(角的和差定义),∴∠DAE=12(180°-∠B-∠C)-(90°-∠B)=90°- 12∠B-12 ∠C-90°+∠B=12(∠B-∠C)(等式性质)
12.1 证明
教学新知
证明:根据已知的真命题,确定某个命题真实性的过程叫做证明.
定理:经过证明的真命题称为定理.
1.经历探索些问题时,由于“直观判断不可靠”、“直观无法做出确定判断”,但运用已有的数学知识和方法可以确定个数学结论的正确性的过程,举反例说明结论的错误性,初步感受说理的必要性.。
知识要点
2.尝试用说理的方法解决问题,在交流中发展有条理思考和有条理表达的能力。
图12.2-8
知识梳理
知识点梳理
知识点:事件的判断.
【例】如图12.2-8,假如用一根比地球赤道长1m的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大(把地球看作球形)?能伸进一根小手指吗?能放进一只拳头吗?
知识梳理
【讲解】解:设地球赤道的周长为c,半径为R1 ,铁丝的半径为R2,
则R2?R1=????+12?????????2????=12????≈0.16(m)
显然,这样的间隙不仅可以伸进一根小手指,而且也能放进一只拳头.
?
【方法小结】不能仅凭表面直觉去判断,计算是检验数学结论常用的方法.
【小练习】如图12.2-9,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大一些?
知识梳理
图12.2-9
【参考答案】直觉上判断第二个大圆内的两个小圆的周长之和大一些.我们可以通过计算来证明.设原来大圆的半径为R,则第一个大圆内的每个小圆的半径为????10,则第一个大圆内的十个小圆的周长之和为10×2????× ????10= 2????????;第二个大圆内的两个小圆的周长之和为2×2????× ????2= 2????????;所以它们的周长一样长.
?
知识梳理
知识点梳理
知识点1:证明与定理.
【例】如图12.2-20,已知AB∥EF,CD∥EF,AB⊥BC,说明CD与BC的位置关系.
图12.2-20
知识梳理
【讲解】∵AB∥EF,CD∥EF(已知),
∴AB∥CD,∠ABC+∠BCD=180°(两直线平行,同旁内角互补),
∵AB⊥BC(已知),
∴∠ABC=90°(垂直的定义).
∴∠BCD=180°-90°=90°(等式的性质),
∴CD⊥BC(垂直的定义).
【方法小结】根据已知条件,再结合要证明的,由果索因,综合推理.
【小练习】
知识梳理
1. 在小括号里填写证明理由:已知:如图12.2-21,点A、O、B在一直线上,OM 平分∠AOC,ON平分∠BOC,求证:OM⊥ON.
图12.2-21
知识梳理
证明: ∵OM平分∠AOC( )
∴∠1=12∠AOC( )
∵ON平分∠BOC( )
∴∠2=12∠BOC( )
∴∠1+∠2=12∠AOC+ 12∠BOC=∠MON ( )
∵A、O、B在一直线上( )
?
已知
角平分线定义
已知
角平分线定义
等式性质
已知
知识梳理
∴∠AOB=180°( )
∴∠1+∠2=12 ×180°= 90°( )
∴OM⊥ON( )
?
平角定义
等量代换
垂直定义
2.如图12.2-22:已知BC平分∠ACD,且∠1=∠2,求证:AB∥CD.
图12.2-22
知识梳理
【参考答案】证明:∵BC平分∠ACD(已知),∴∠1=∠BCD(角平分线定义),∵∠1=∠2(已知),∴∠2=∠BCD(等量代换),∴AB∥CD( 内错角相等,两直线平行).
知识点梳理
知识点1:三角形内角和定理的应用.
【例】如图12.2-40,在△ABC中,∠ABC,∠ACB的平分线交于点O,求证:∠BOC=90°??12∠A.
?
知识梳理
【讲解】∵BO,CO分别是∠ABC和∠ACB的平分线(已知),
∴∠ABC=2∠OBC,∠ACB=2∠OCB(角平分线定义),
又在△BOC中,∠BOC+∠OBC+∠OCB=180°(三角形内角和等于180°),
∴∠BOC+12∠ABC+12∠ACB=180°(等量代换),
又∵在△ABC中,∠A+∠ABC+∠ACB=180°(三角形内角和等于180°),
∴∠BOC=12∠A+90°(等式性质).
?
图12.2-40
知识梳理
【方法小结】紧扣三角形内角和等于180°,并能把∠OBC与∠OCB的和视为整体处理.
【小练习】
已知:如图12.2-41,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:∠P=90°.
【参考答案】证明:∵AB∥CD(已知),
∴∠BEF+∠DFE=180°
(两直线平行,同旁内角互补).
图12.2-41
知识梳理
又∵∠BEF的平分线与∠DFE的平分线相交于点P(已知),
∴∠PEF=12∠BEF,∠PFE=12∠DEF
(角平分线定义),
∴∠PEF+∠PFE=12(∠BEF+∠DFE)=90°(等式性质).
∵∠PEF+∠PFE+∠P=180°
(三角形内角和等于180°),
∴∠P=90°(等式性质).
?
图12.2-42
知识梳理
知识点2: 三角形内角和定理的推论
【例】已知:如图12.2-42,AM,CM分别平分∠BAD和∠BCD,
试说明∠M= 12 (∠B+∠D).
?
知识梳理
【讲解】证明:∵AM,CM分别平分∠BAD和∠BCD(已知),
∴∠BAM=∠MAD,∠MCB=∠MCD(角平分线定义),
∵∠ANC=∠B+∠BAM=∠M+∠MCB、
∠AEC=∠MCD+∠D=∠MAD+∠M( 三角形的外角等于和它不相邻的两个内角的和),
∴∠M=∠B+∠BAM-∠MCB①,
∠M=∠MCD+∠D-∠MAD②(等式性质),
∴①+②得:2∠M=∠B+∠D(等式性质),
∴∠M= 12 (∠B+∠D)(等式性质).
?
知识梳理
【方法小结】运用三角形内角和定理的推论来转化。
【小练习】
已知如图12.2-43,在△ABC中,CH是外角∠ACD的平分线,BH是∠ABC的平分线.
求证:∠A=2∠H.
图12.2-43
知识梳理
【参考答案】证明:∵∠ACD是△ABC的一个外角(已知),
∴∠ACD=∠ABC+∠A( 三角形的外角等于和它不相邻的两个内角的和)
∵∠2是△BCD的一个外角(已知),
∴∠2=∠1+∠H( 三角形的外角等于和它不相邻的两个内角的和)
∵CH是外角∠ACD的平分线,BH是∠ABC的平分线(已知)
∴∠1= 12 ∠ABC,∠2= 12 ∠ACD(角平分线性质 )
∴∠A=∠ACD-∠ABC=2(∠2-∠1)(等式的性质)
而∠H=∠2-∠1(等式的性质)
?
知识梳理
中考在线
考点:简单的证明、推理 .
【例】(2015台州)某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是(?? )
A.若甲对,则乙对??? B.若乙对,则甲对? C.若乙错,则甲错??
D.若甲粗,则乙对
D
知识梳理
【讲解】 假设甲说的对,则参加两种比赛的人次大于28,因为共有20位同学,因此两项都参加的人数大于8人次,故乙说的错误;
假设乙说的对,则参加两种比赛的人次小于25,因为共有20位同学,因此只参加一项的人数不大于12人,故甲说法错误;
故选:D.
【方法小结】分两种情况分别进行分析/推理与论证.
【实战演练】
1. (2014河北)如图12.2-44,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是( )。
B
知识梳理
A.20° B.30° C.70° D.80°
2.(2014?永州)小聪,小玲,小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有A、B两个选项,且只有一个选项是正确的,三人的答案和得分如下表,试问:这五道题的正确答案(按1~5题的顺序排列)是_____________________.
BABBA
知识梳理
{5940675A-B579-460E-94D1-54222C63F5DA}题号
答案
选手
1
2
3
4
5
得分
小聪
B
A
A
B
A
40
小玲
B
A
B
A
A
40
小红
A
B
B
B
A
30
3. (2014年湖北随州)将一副直角三角板如图12.2-45放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 度.
75
知识梳理
图12.2-45
4. (2014年福建厦门)A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权,比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队
知识梳理
(有且只有两个队)出线,小组赛结束后,如果A队没有全胜,那么A队的积分至少要几分才能保证一定出线?请说明理由.
[注:单循环比赛就是小组内的每一个队都要和其他队赛一场].
【参考答案】 A队的积分至少要7分才能保证一定出线。
课堂练习
1. 今年五一节期间,王老板在其经营的服装店里卖出两件衣服,其中一件是裤子售价为168元,盈利20%,一件是夹克衫售价也是168元,但亏损20%,问王老板在这次的交易过程中是赚了还是亏了,( ).
A.赚了 B.亏了 C.不赚不亏 D.无法确定
B
2.如图12.2-46,在△ABC中,∠B=67°,∠C=33°,AD是△ABC
的角平分线,则∠CAD的度数为( )
A.40° B.45° C.50° D.55°
A
课堂练习
图12.2-46
3.(2013?泉州)在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
D
课堂练习
4.你认为图12.2-12中,大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大一些?请你猜一猜,并用学过的知识和数学方法验证你的猜想.
图12.2-12
【参考答案】周长相等。
课堂练习
5. 两个连续奇数的平方差能被8整除吗?请说明你的理由.
【参考答案】两个连续奇数的平方差能被8整除.理由:设这两个连续奇数分别为:(2n+1)与(2n-1),∵(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=4n×2=8n.
∴两个连续奇数的平方差能被8整除.
6. 如图12.2-24,若∠3=∠4,你能说明AD∥BC,AB∥DC吗?
小亮回答:都行,∵∠3=∠4,∴AD∥BC,AB∥DC.
课堂练习
图12.2-24
小亮错在哪里,请指出错因,并改正.
【参考答案】1.解:∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),由于没有其它条件不能识别AD∥BC
课堂练习
7.根据提示,同桌合作,完成括号内的依据.
如图12.2-25,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
图12.2-25
课堂练习
证明:BE∥DF.理由如下:
∵∠A=∠C=90°( ),
∴∠ABC+∠ADC=180°( ).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=12∠ABC,∠3=∠4=12∠ADC( ).
∴∠1+∠3=12(∠ABC+∠ADC)=12×180°=90°(等量代换).
又∠1+∠AEB=90°(三角形的内角和等于180°),
?
已知
四边形的内角和等于360°
角平分线的定义
课堂练习
∴∠3=∠AEB(等量代换).
∴ (同位角相等,两直线平行).
BE∥DF
8. 如图12.2-49,已知AB∥CD,求证:∠B+∠D=∠BED.
图12.2-49
课堂练习
【参考答案】(方法不惟一)如图12.2-50, 过E点作EF∥AB,(已作),∴∠1=∠B,(两直线平行,内错角相等),又∵AB∥CD,(已知),∴EF∥CD,∴∠2=∠D,∴∠B+∠D=∠1+∠2,∴∠BED=∠B+∠D.(等量代换)
图12.2-50
课后习题
1. 图12.2-13中,有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心0按逆时针方向进行旋转,每次均旋转45.,第1次旋转后得到图(1),第2次旋转后得到图(2),…,则第10次旋转后得到的图形与图(1)~(4)中相同的是( ).
图12.2-13
B
课后习题
2.对于图12.2-27中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180°
图12.2-27
D
课后习题
3. (2012?长春)如图12.2-51,在Rt△ABC中,∠C=90°.D为边CA延长线上一点,DE∥AB,∠ADE=42°,则∠B的大小为( )
图12.2-51
A.42° B.45° C.48° D.58°
C
课后习题
4. 观察后测量图12.2-14中a,b,c,d四条直线, 。
图12.2-14
a ∥ c
课后习题
5. 如图12.2-28,AB∥CD,∠B=∠C,求证:AC∥BD.
图12.2-28
证明:∵AB∥CD( ),
∴∠A+∠C=180°( ),
已知
两直线平行,同旁内角互补
课后习题
又∵∠B=∠C( ),
∴∠A+∠B=180°( ),
∴AC∥BD( ).
已知
等量代换
同旁内角互补,两直线平行
6.如图12.2-31,AB∥CD,直线MN分别叫AB,CD于点E、F.EG平分∠AEF,EG⊥FG于点G,若∠BEM=50°,则∠CFG= °.
图12.2-31
65
课后习题
7.如图12.2-53,∠1是Rt△ABC的一个外角,直线DE∥BC,分别交边AB、AC于点D、E,∠1=120°,则∠2的度数是 .
图12.2-53
30°
课后习题
8. 若一个正整数能表示为两个连续偶数的平方差,那么这个正整数为“神秘数”.如4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数
(1)28和76是神秘数吗?为什么?
(2)设两个连续偶数为2k+2和2k(k为非负整数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?
课后习题
【参考答案】 (1)是,∵28=82-62,76=202-182.(2)是,∵(2k+2)2-(2k)2=8k+4=4(2k+1),
∴由这两个连续偶数构成的神秘数是4的倍数
9. 如图12.2-17,请你观察,黑白方格间的横线平行吗?先猜想,然后利用合适的方法验证你的猜想.
图12.2-17
课后习题
【参考答案】通过观察黑白方格间的横线不平行,用三角板和直尺验证后发现他们是平行的.
10. 已知:如图12.2-32,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.求证:AB∥CD.
【参考答案】证明:∵GH⊥CD(已知)∴∠CHG=90°(垂直定义).又∵∠2=30°(已知),∴∠3=60°.∴∠4=60°(对顶角相等).又∵∠1=60°(已知),∴∠1=∠4.∴AB∥CD(同位角相等,两直线平行)
课后习题
图12.2-32
11. 已知,如图12.2-55,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.求证:∠DAE=12(∠B-∠C)
?
课后习题
图12.2-55
【参考答案】由图知,∵∠BAC+∠B+∠C =180°(三角形内角和等于180°),∴∠BAC=180°-∠B-∠C(等式性质),∵AD是BC边上的高(已知),∴∠ADB=90°(三角形高的定义),∵∠BAD+∠B+∠ADB=180°(三角形内角和等于180°),∴∠BAD=180°-∠B-∠ADB=90°-∠B(等
课后习题
式性质),∵AE平分∠BAC(已知),∴∠BAE=12∠BAC(角平分线定义),∵∠DAE=∠BAE-∠BAD(角的和差定义),∴∠DAE=12(180°-∠B-∠C)-(90°-∠B)=90°- 12∠B-12 ∠C-90°+∠B=12(∠B-∠C)(等式性质)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
