12.2 互逆命题-2021春苏科版七年级数学下册课件(共29张PPT)
文档属性
| 名称 | 12.2 互逆命题-2021春苏科版七年级数学下册课件(共29张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 532.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览








文档简介
第十二章 证明
12.1 互逆命题
课题引入
在公元前6世纪,古希腊哲人泰勒斯利用影子测量了金字塔的高度.
据说,埃及的大金字塔修成一千多年后,还没有人能够准确的测出它的高度。有不少人作过很多努力,但都没有成功。
课题引入
c
b
a
A
B
C
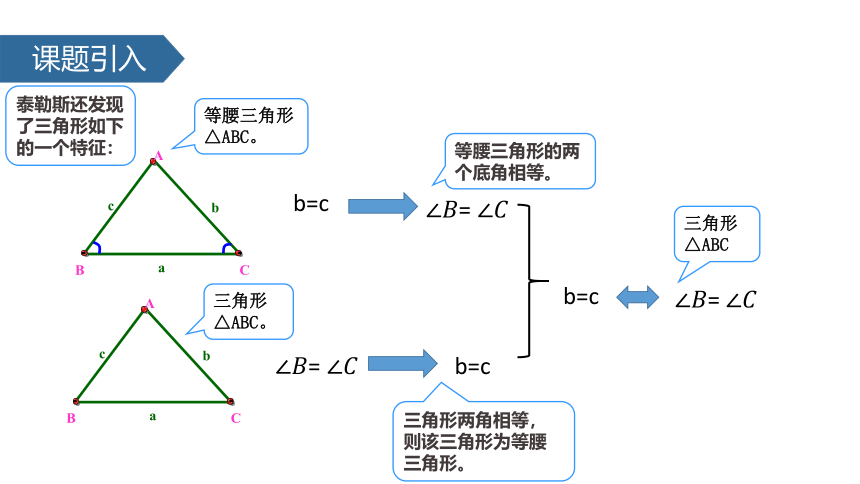
泰勒斯还发现了三角形如下的一个特征:
三角形△ABC
等腰三角形△ABC。
b=c
∠????= ∠????
?
c
b
a
A
B
C
三角形△ABC。
b=c
∠????= ∠????
?
b=c
∠????= ∠????
?
等腰三角形的两个底角相等。
三角形两角相等,则该三角形为等腰三角形。
教学新知
互逆命题:在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题是另一个命题的逆命题.
知识要点
1.引导学生通过具体实例,了解原命题及其逆命题的概念;会识别两个互逆命题,知道原命题成立其逆命题不一定成立;通过具体的例子了解反例的作用,知道利用反例可以证明一个命题是错误的。
2.经历构造一个命题的逆命题,并证明这个逆命题是真命题,获得新的数学结论的过程,学习逆向思考研究问题。
知识梳理
知识点梳理
知识点1:互逆命题.
【例】写出下列命题的逆命题,并判断其逆命题的真假.
(1)两直线平行,同位角相等;
(2)如果两个角都是直角,那么它们相等;
(3)如果x=1,那么|x|=1。
【讲解】(1)的逆命题:同位角相等,两直线平行,它是一个真命题;
(2)的逆命题:如果两个角相等,那么这两个角都是直角,它是一个假命题;
(3)的逆命题:如果|x|=1 ,那么x=1,它是一个假命题。
知识梳理
【方法小结】解题时应先分清原命题的条件和结论,再将其交换位置,但有时要适当改变形式,使条件和结论都能单独成句.
【小练习】
1. 给出下列命题:
(1) 直角都相等 ;(2) 同位角相等,两直线平行; (3)如果a+b>0, 那么a>0,b>0;(4)两直线平行,同位角相等;(5)相等的角都是直角;(6)如果a>0,b>0,那么ab>0,其中,互为逆命题的是:________________________________.
(1)与(5)、(2)与(4)、(3)与(60
知识梳理
2. 写出下列命题的逆命题.
(1)和为180°的两个角互为补角
(2)同旁内角互补
【参考答案】:(1)互为补角的两个角和为180°.(2)互补的两个角是同旁内角.
知识点2: 反例.
【例】举反例说明下列命题是假命题:
(1)如果a+b>0,那么a>0,b>0;(2)两个锐角的和大于90°
知识梳理
【讲解】 (1)a=5,b=-2时,有a+b=5+(-2)=3,但b=-2<0;(2)30°的锐角与40°的锐角有30°+40°=70°<90°.
【方法小结】注意满足条件的例子有多种可能,要在这几种可能中找出符合条件且结论不成立的例子.
【小练习】
判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
知识梳理
【参考答案】(1)假:若两角都是40°的角,未必是对顶角(2)假:若a=0,b=2,不成立
知识点梳理
知识点:平行线的推论.
【例】(2014春?无锡期末)已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两条直线平行;⑤邻补角的平分线互相垂直.其中真命题的个数为( )
A.3个 B.2个 C.1个 D.0个
B
知识梳理
【讲解】①对顶角既要考虑大小,还要考虑位置,相等的角不一定是对顶角,故①错误;
②互补的角不一定是邻补角,所以不一定是平角,故②错误;
③互补的两个角也可以是两个直角,故③错误;
④平行于同一条直线的两条直线平行,是平行公理,故④正确;
⑤邻补角的平分线的夹角正好是平角的一半,是直角,所以互相垂直,故⑤正确.
所以真命题有④⑤两个.
知识梳理
【方法小结】准确掌握平行公理及推论;对顶角、邻补角;平行线的判定.
【小练习】
1.(2014春?铜陵期末)下列说法正确的是( )
A. 同位角相等
B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角
D. 在同一平面内,如果a∥b,b∥c,则a∥c
D
知识梳理
2.(2014春?i东海期末)或若直线a∥b,b∥c,则 ,理由是 。
a∥c
平行于同一条直线的两条直线平行
中考在线
考点:命题的真假及互逆.
【例】(2014?襄阳)下列命题错误的是( )
A.所有的实数都可用数轴上的点表示 B.等角的补角相等
C.无理数包括正无理数,0,负无理数 D.两点之间,线段最短
C
知识梳理
【讲解】解:A、所有的实数都可用数轴上的点表示,所以A选项的说法正确;B、等角的补角相等,所以B选项的说法正确;C、无理数包括正无理数和负无理,所以C选项的说法错误;D、两点之间,线段最短,所以D选项的说法正确.故选C.
【方法小结】一一进行判断,不对的可以举反例。
【实战演练】
1. (2012?内蒙古包头改)已知下列命题:
①若a≤0,则|a|=-a ②若ma2>na2,则m>n; 其中原命题与逆命题均为真命题的个数是( )
C
知识梳理
A. 0个 B.1个 C.2个 D.3个
2.(2012?温州)下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=-2 B.a=-1 C.a=1 D.a=2
A
课堂练习
1.以下说法中,正确的有( )个。
(1) 每一个命题都有逆命题.
(2) 如果原命题是真命题,那么它的逆命题也一定是真命题.
(3) 原命题是假命题,但它的逆命题可能是真命题.
A. 1 B. 2 C. 3 D.0
2. 下列命题: ①同旁内角互补,两直线平行;②直角都相等;③锐角的补角是钝角;④若ab>0且a+b>0,则a>0且b>0.它们的逆命题是真命题的个数是( ).
B
C
课堂练习
3.命题“锐角小于90度”的逆命题是( ).
A.如果这个角是锐角,那么这个角小于90度
B.不是锐角的角不小于90度
C.不小于90度的角不是锐角
D.小于90度的角是锐角
A.1个 B.2个 C.3个 D.4个
D
4. “如果|a|=|b|,那么a=b.”的逆命题是
。
如果a=b,
那么|a|=|b|
课堂练习
5. 给出下列命题:
(1)对顶角相等;(2)同位角相等,两直线平行;(3)如果a+b>0,那么a>0,b>0; (4)两直线平行,同位角相等;(5)相等的角都是对顶角;(6)如果a>0,b>0, 那么ab>0.其中,互为逆命题的是:____________________________.
(1)和(5),(2)和(4)
6. “直角三角形的两锐角互余“的逆命题是 命题(填“真”或“假”)。
真
课堂练习
7.命题:“如果|a|=|b|,那么a=b”的逆命题为_______
__________________________,逆命题是______命题.(填“真”或“假”).
如果
a=b,那么|a|=|b|
真
8. 写出下列命题的逆命题,并判断原命题与逆命题的真假.
(1) 如果a>0,那么a2>0;(2) 如果ac2>bc2,那么a>b.
【参考答案】(1) 如果a2>0,那么a>0;原命题真,逆命题假;(2);如果a>b,那么ac2>bc2;原命题真,逆命题假.
课堂练习
9.如图12.3-6,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,(1)求证:∠A+∠B=180°;(2)找出互逆命题的理论依据.
图12.3-6
课堂练习
【参考答案】∵CE,DE分别平分∠BCD,∠ADC(已知),∴∠ADC=2∠1,∠BCD=2∠2(角平分线性质)
又∵∠1+∠2=90°(已知),∴∠ADC+∠BCD=2(∠1+∠2)=180°( 等式性质),
∴AD∥BC(同旁内角互补,两直线平行),∴∠A+∠B=180°(两直线平行,同旁内角互补).
“同旁内角互补,两直线平行”与 “两直线平行,同旁内角互补”是互逆命题.
课后习题
1. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α
B.∠α=90°,∠α的补角∠β=900°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α
D.两个角互为邻补角
2. 下面有2句话:(1)真命题的逆命题一定是真命题;(2)假命题的逆命题不一定是假命题,其中,正确的( ).
C
B
课后习题
3.命题“2的平方等于4”的逆命题的是( ).
A. 2的平方等于4 B.平方等于4的数是 2
C.平方等于4的数是±2 D.平方等于4的数是2
A.只有(1) B.只有(2) C.只有(1)和(2) D.一个也没有
D
4. 如图12.3-8,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )
A.50° B.60° C.65° D.90°
C
课后习题
图12.3-8
5.(2011年德州)下列命题中,其逆命题成立的是 (只填写序号).
①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等; ③如果两个实数相等,那么它们的平方相等。
①
课后习题
6. 命题:①直角都相等;②若ab>0且a+b>0,则a>0且b>0;③一个角的补角大于这个角.其中原命题和逆命题都为真命题的有 .
7.请写出一个命题,使其是假命题而它的逆命题是真命题,命题是 。
8. 在同一平面内,如果a∥b,b∥c,则a与c的位置关系是 .
②
对顶角相等(答案不唯一)
平行
4. 举反例说明下列命题是假命题:
课后习题
(1)任何数的平方大于0;(2)两个锐角的和是钝角;(3)一个角的补角一定大于这个角;
【参考答案】:(1)这个数为0;(2)这两个角分别为30°,45°,和为75°;(3)若这个角是直角,补角和它相等
9.如图12.3--3,现有以下3句话:①a⊥c,②b⊥c,③a∥b.请以其中2句话为条件,第三句话为结论构造命题.
(1) 你构造的是哪几个命题?
(2) 你构造的命题是真命题还是假命题?请加以证明.
课后习题
图12.3-3
【参考答案】:(1)可以组合为3个命题,分别是:若a⊥c,b⊥c,则a∥b;若b⊥c,a∥b,则a⊥c;若a⊥c,a∥b,则b⊥c.(2)①若a⊥c,b⊥c,则a∥b;证明:因为a⊥c,b⊥c,
所以∠1=∠2=90°,所以a∥b.②若b⊥c,a∥b,则a⊥c;证明:因为
课后习题
b⊥c,所以∠2=90°.因为a∥b,所以∠1=∠2=90°.所以a⊥c.③若a⊥c,a∥b,则b⊥c.
证明:因为a⊥c,所以∠1=90°.因为a∥b,所以∠2=∠1=90°.所以b⊥c.
10.如图12.3-9,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,
求证:EF也是∠AED的平分线.
【参考答案】: ∵BD是∠ABC的平分线(已知),∴∠ABD=∠DBC(角平分线定义);∵ED∥BC(已知),∴∠BDE=∠DBC(两直线平行,内错角相等),∴∠ABD=∠BDE(等量代换);又∵∠FED=∠BDE(已知),
课后习题
∴EF∥BD(内错角相等,两直线平行),∴∠AEF=∠ABD(两直线平行,同位角相等),∴∠AEF=∠DEF(等量代换),∴EF是∠AED的平分线(角平分线定义)
图12.3-9
12.1 互逆命题
课题引入
在公元前6世纪,古希腊哲人泰勒斯利用影子测量了金字塔的高度.
据说,埃及的大金字塔修成一千多年后,还没有人能够准确的测出它的高度。有不少人作过很多努力,但都没有成功。
课题引入
c
b
a
A
B
C
泰勒斯还发现了三角形如下的一个特征:
三角形△ABC
等腰三角形△ABC。
b=c
∠????= ∠????
?
c
b
a
A
B
C
三角形△ABC。
b=c
∠????= ∠????
?
b=c
∠????= ∠????
?
等腰三角形的两个底角相等。
三角形两角相等,则该三角形为等腰三角形。
教学新知
互逆命题:在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题是另一个命题的逆命题.
知识要点
1.引导学生通过具体实例,了解原命题及其逆命题的概念;会识别两个互逆命题,知道原命题成立其逆命题不一定成立;通过具体的例子了解反例的作用,知道利用反例可以证明一个命题是错误的。
2.经历构造一个命题的逆命题,并证明这个逆命题是真命题,获得新的数学结论的过程,学习逆向思考研究问题。
知识梳理
知识点梳理
知识点1:互逆命题.
【例】写出下列命题的逆命题,并判断其逆命题的真假.
(1)两直线平行,同位角相等;
(2)如果两个角都是直角,那么它们相等;
(3)如果x=1,那么|x|=1。
【讲解】(1)的逆命题:同位角相等,两直线平行,它是一个真命题;
(2)的逆命题:如果两个角相等,那么这两个角都是直角,它是一个假命题;
(3)的逆命题:如果|x|=1 ,那么x=1,它是一个假命题。
知识梳理
【方法小结】解题时应先分清原命题的条件和结论,再将其交换位置,但有时要适当改变形式,使条件和结论都能单独成句.
【小练习】
1. 给出下列命题:
(1) 直角都相等 ;(2) 同位角相等,两直线平行; (3)如果a+b>0, 那么a>0,b>0;(4)两直线平行,同位角相等;(5)相等的角都是直角;(6)如果a>0,b>0,那么ab>0,其中,互为逆命题的是:________________________________.
(1)与(5)、(2)与(4)、(3)与(60
知识梳理
2. 写出下列命题的逆命题.
(1)和为180°的两个角互为补角
(2)同旁内角互补
【参考答案】:(1)互为补角的两个角和为180°.(2)互补的两个角是同旁内角.
知识点2: 反例.
【例】举反例说明下列命题是假命题:
(1)如果a+b>0,那么a>0,b>0;(2)两个锐角的和大于90°
知识梳理
【讲解】 (1)a=5,b=-2时,有a+b=5+(-2)=3,但b=-2<0;(2)30°的锐角与40°的锐角有30°+40°=70°<90°.
【方法小结】注意满足条件的例子有多种可能,要在这几种可能中找出符合条件且结论不成立的例子.
【小练习】
判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
知识梳理
【参考答案】(1)假:若两角都是40°的角,未必是对顶角(2)假:若a=0,b=2,不成立
知识点梳理
知识点:平行线的推论.
【例】(2014春?无锡期末)已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两条直线平行;⑤邻补角的平分线互相垂直.其中真命题的个数为( )
A.3个 B.2个 C.1个 D.0个
B
知识梳理
【讲解】①对顶角既要考虑大小,还要考虑位置,相等的角不一定是对顶角,故①错误;
②互补的角不一定是邻补角,所以不一定是平角,故②错误;
③互补的两个角也可以是两个直角,故③错误;
④平行于同一条直线的两条直线平行,是平行公理,故④正确;
⑤邻补角的平分线的夹角正好是平角的一半,是直角,所以互相垂直,故⑤正确.
所以真命题有④⑤两个.
知识梳理
【方法小结】准确掌握平行公理及推论;对顶角、邻补角;平行线的判定.
【小练习】
1.(2014春?铜陵期末)下列说法正确的是( )
A. 同位角相等
B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角
D. 在同一平面内,如果a∥b,b∥c,则a∥c
D
知识梳理
2.(2014春?i东海期末)或若直线a∥b,b∥c,则 ,理由是 。
a∥c
平行于同一条直线的两条直线平行
中考在线
考点:命题的真假及互逆.
【例】(2014?襄阳)下列命题错误的是( )
A.所有的实数都可用数轴上的点表示 B.等角的补角相等
C.无理数包括正无理数,0,负无理数 D.两点之间,线段最短
C
知识梳理
【讲解】解:A、所有的实数都可用数轴上的点表示,所以A选项的说法正确;B、等角的补角相等,所以B选项的说法正确;C、无理数包括正无理数和负无理,所以C选项的说法错误;D、两点之间,线段最短,所以D选项的说法正确.故选C.
【方法小结】一一进行判断,不对的可以举反例。
【实战演练】
1. (2012?内蒙古包头改)已知下列命题:
①若a≤0,则|a|=-a ②若ma2>na2,则m>n; 其中原命题与逆命题均为真命题的个数是( )
C
知识梳理
A. 0个 B.1个 C.2个 D.3个
2.(2012?温州)下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=-2 B.a=-1 C.a=1 D.a=2
A
课堂练习
1.以下说法中,正确的有( )个。
(1) 每一个命题都有逆命题.
(2) 如果原命题是真命题,那么它的逆命题也一定是真命题.
(3) 原命题是假命题,但它的逆命题可能是真命题.
A. 1 B. 2 C. 3 D.0
2. 下列命题: ①同旁内角互补,两直线平行;②直角都相等;③锐角的补角是钝角;④若ab>0且a+b>0,则a>0且b>0.它们的逆命题是真命题的个数是( ).
B
C
课堂练习
3.命题“锐角小于90度”的逆命题是( ).
A.如果这个角是锐角,那么这个角小于90度
B.不是锐角的角不小于90度
C.不小于90度的角不是锐角
D.小于90度的角是锐角
A.1个 B.2个 C.3个 D.4个
D
4. “如果|a|=|b|,那么a=b.”的逆命题是
。
如果a=b,
那么|a|=|b|
课堂练习
5. 给出下列命题:
(1)对顶角相等;(2)同位角相等,两直线平行;(3)如果a+b>0,那么a>0,b>0; (4)两直线平行,同位角相等;(5)相等的角都是对顶角;(6)如果a>0,b>0, 那么ab>0.其中,互为逆命题的是:____________________________.
(1)和(5),(2)和(4)
6. “直角三角形的两锐角互余“的逆命题是 命题(填“真”或“假”)。
真
课堂练习
7.命题:“如果|a|=|b|,那么a=b”的逆命题为_______
__________________________,逆命题是______命题.(填“真”或“假”).
如果
a=b,那么|a|=|b|
真
8. 写出下列命题的逆命题,并判断原命题与逆命题的真假.
(1) 如果a>0,那么a2>0;(2) 如果ac2>bc2,那么a>b.
【参考答案】(1) 如果a2>0,那么a>0;原命题真,逆命题假;(2);如果a>b,那么ac2>bc2;原命题真,逆命题假.
课堂练习
9.如图12.3-6,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,(1)求证:∠A+∠B=180°;(2)找出互逆命题的理论依据.
图12.3-6
课堂练习
【参考答案】∵CE,DE分别平分∠BCD,∠ADC(已知),∴∠ADC=2∠1,∠BCD=2∠2(角平分线性质)
又∵∠1+∠2=90°(已知),∴∠ADC+∠BCD=2(∠1+∠2)=180°( 等式性质),
∴AD∥BC(同旁内角互补,两直线平行),∴∠A+∠B=180°(两直线平行,同旁内角互补).
“同旁内角互补,两直线平行”与 “两直线平行,同旁内角互补”是互逆命题.
课后习题
1. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α
B.∠α=90°,∠α的补角∠β=900°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α
D.两个角互为邻补角
2. 下面有2句话:(1)真命题的逆命题一定是真命题;(2)假命题的逆命题不一定是假命题,其中,正确的( ).
C
B
课后习题
3.命题“2的平方等于4”的逆命题的是( ).
A. 2的平方等于4 B.平方等于4的数是 2
C.平方等于4的数是±2 D.平方等于4的数是2
A.只有(1) B.只有(2) C.只有(1)和(2) D.一个也没有
D
4. 如图12.3-8,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )
A.50° B.60° C.65° D.90°
C
课后习题
图12.3-8
5.(2011年德州)下列命题中,其逆命题成立的是 (只填写序号).
①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等; ③如果两个实数相等,那么它们的平方相等。
①
课后习题
6. 命题:①直角都相等;②若ab>0且a+b>0,则a>0且b>0;③一个角的补角大于这个角.其中原命题和逆命题都为真命题的有 .
7.请写出一个命题,使其是假命题而它的逆命题是真命题,命题是 。
8. 在同一平面内,如果a∥b,b∥c,则a与c的位置关系是 .
②
对顶角相等(答案不唯一)
平行
4. 举反例说明下列命题是假命题:
课后习题
(1)任何数的平方大于0;(2)两个锐角的和是钝角;(3)一个角的补角一定大于这个角;
【参考答案】:(1)这个数为0;(2)这两个角分别为30°,45°,和为75°;(3)若这个角是直角,补角和它相等
9.如图12.3--3,现有以下3句话:①a⊥c,②b⊥c,③a∥b.请以其中2句话为条件,第三句话为结论构造命题.
(1) 你构造的是哪几个命题?
(2) 你构造的命题是真命题还是假命题?请加以证明.
课后习题
图12.3-3
【参考答案】:(1)可以组合为3个命题,分别是:若a⊥c,b⊥c,则a∥b;若b⊥c,a∥b,则a⊥c;若a⊥c,a∥b,则b⊥c.(2)①若a⊥c,b⊥c,则a∥b;证明:因为a⊥c,b⊥c,
所以∠1=∠2=90°,所以a∥b.②若b⊥c,a∥b,则a⊥c;证明:因为
课后习题
b⊥c,所以∠2=90°.因为a∥b,所以∠1=∠2=90°.所以a⊥c.③若a⊥c,a∥b,则b⊥c.
证明:因为a⊥c,所以∠1=90°.因为a∥b,所以∠2=∠1=90°.所以b⊥c.
10.如图12.3-9,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,
求证:EF也是∠AED的平分线.
【参考答案】: ∵BD是∠ABC的平分线(已知),∴∠ABD=∠DBC(角平分线定义);∵ED∥BC(已知),∴∠BDE=∠DBC(两直线平行,内错角相等),∴∠ABD=∠BDE(等量代换);又∵∠FED=∠BDE(已知),
课后习题
∴EF∥BD(内错角相等,两直线平行),∴∠AEF=∠ABD(两直线平行,同位角相等),∴∠AEF=∠DEF(等量代换),∴EF是∠AED的平分线(角平分线定义)
图12.3-9
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
