苏科版 八年级下册 9.2 中心对称与中心对称图形 课件(共25张PPT)
文档属性
| 名称 | 苏科版 八年级下册 9.2 中心对称与中心对称图形 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 253.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览




文档简介
9.2 中心对称与中心对称图形
【学习目标】
1.通过与轴对称和轴对称图形类比,
理解中心对称和中心对称图形的概念和有关性质;
2.会画一个图形关于某点对称的图形;
3.经历观察、操作、思考、探究中心对称图形的有关概念和基本性质的过程,感受对称、匀称、均衡的美感,积累一定的审美体验。
情境创设
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
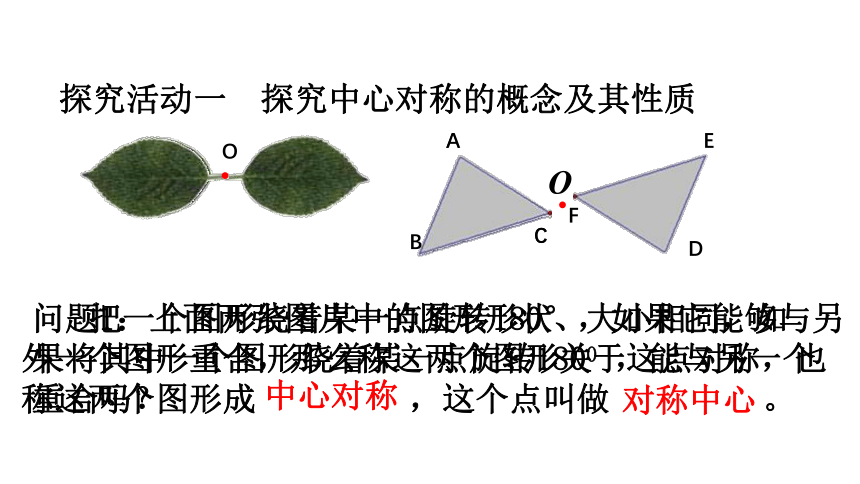
探究活动一 探究中心对称的概念及其性质
问题1:上面两张图片中的图形形状、大小相同,如果将其中一个图形绕着某一点旋转1800 ,能与另一个重合吗?
O
A
C
E
F
A
C
O
B
D
把一个图形绕着某一点旋转180°,如果它能够与另外一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成 ,这个点叫做 。
中心对称
对称中心
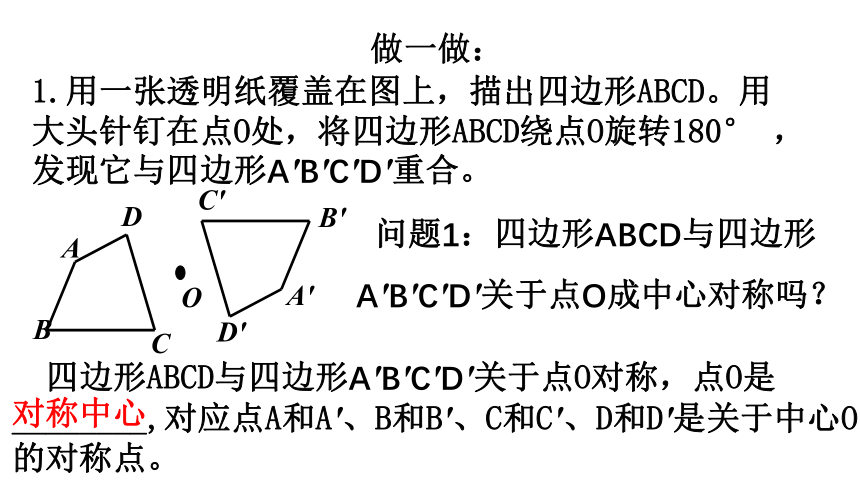
1.用一张透明纸覆盖在图上,描出四边形ABCD。用大头针钉在点O处,将四边形ABCD绕点O旋转180° ,发现它与四边形A'B'C'D'重合。
四边形ABCD与四边形A'B'C'D'关于点O对称,点O是________,对应点A和A'、B和B'、C和C'、D和D'是关于中心O
的对称点。
做一做:
C'
O
A
B
C
D
A'
B'
D'
问题1:四边形ABCD与四边形A'B'C'D'关于点O成中心对称吗?
对称中心
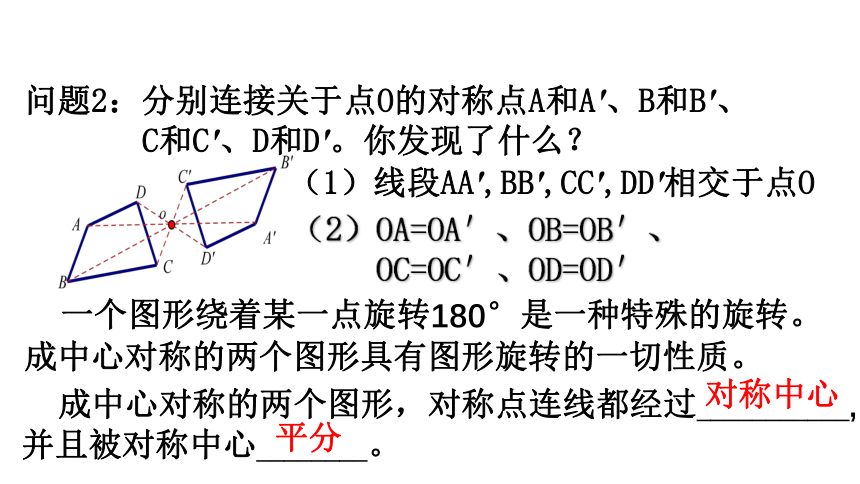
问题2:分别连接关于点O的对称点A和A'、B和B'、
C和C'、D和D'。你发现了什么?
一个图形绕着某一点旋转180°是一种特殊的旋转。
成中心对称的两个图形具有图形旋转的一切性质。
成中心对称的两个图形,对称点连线都经过___________, 并且被对称中心________。
对称中心
平分
(1)线段AA',BB',CC',DD'相交于点O
(2)OA=OA′、OB=OB′、
OC=OC′、OD=OD′
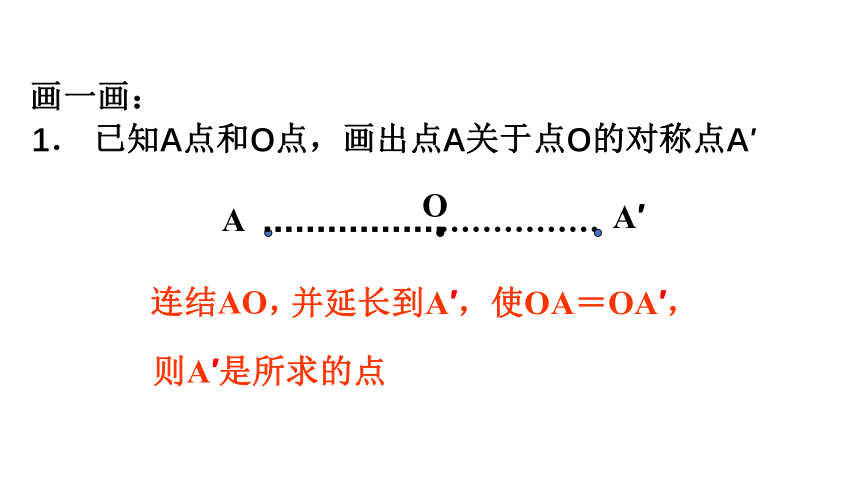
1. 已知A点和O点,画出点A关于点O的对称点A′
画一画:
A
O
A′
连结AO,
并延长到A′,使OA=OA′,
则A′是所求的点
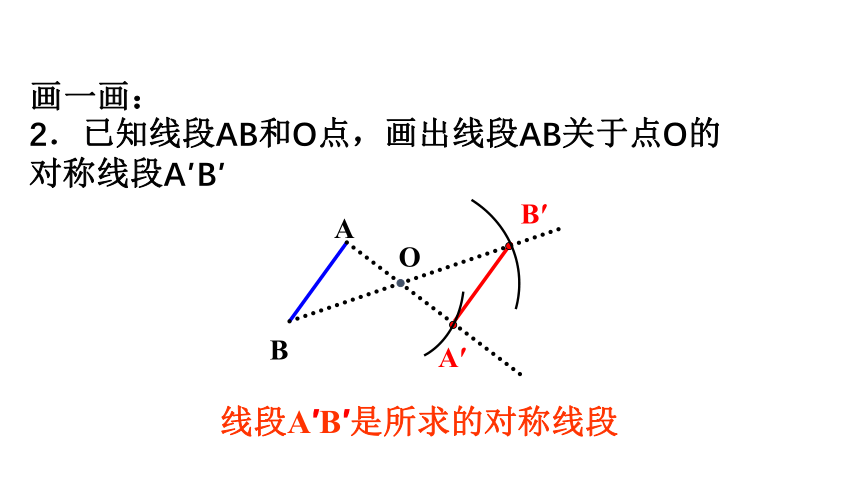
2.已知线段AB和O点,画出线段AB关于点O的
对称线段A′B′
画一画:
A
A′
B′
B
O
线段A′B′是所求的对称线段
3.已知ΔABC和点0,画ΔA′B′C′,使它与ΔABC关于点0成中心对称。
画一画:
ΔA′B′C′是所求的三角形
A′
C′
B′
C
A
B
O
变式:
1.D是ΔABC的边AC上的一点,
画ΔEFG,使它与ΔABC关于
点D成中心对称。
B
C
A
D
E
F
G
ΔEFG是所求的三角形
2.D是ΔABC内部的一点,画ΔA′B′C′,使它与ΔABC关于点D成中心对称。
变式:
A′
B′
C′
ΔA′B′C′是所求的三角形
3.如图,已知△ABC与△A′B′C′中心对称,请确定其对称中心O。
变式:
A
B
C
A′
B′
C′
O
下列图案有什么共同特征
探究活动二 探究中心对称图形的特征
(1)
(2)
(3)
(4)
旋转图形(1)
旋转图形(2)
旋转图形(3)
旋转图形(4)
旋转
平面内,如果把一个图形绕着某一点旋转180°后能与自身重合,那么这个图形叫做中心对称图形。这个点就是它的对称中心。
探究活动二 探究中心对称图形的特征
中心对称和中心对称图形既有区别又有联系
(1)中心对称图形有一个对称中心,将这个图形绕对称中心旋转180°,旋转后的图形能与原来的图形重合;
(2)中心对称图形是对一个图形来说的,是一个图形所具有的性质;
(3)如果将成中心对称的两个图形看成一个图形,那么这个图形的整体就是中心对称图形;反过来,如果将一个中心对称图形沿过对称中心的任一条直线分成两个图形,那么这两个图形成中心对称.
2.在①线段、②角、 ③等腰三角形、④ 正方形、
⑤圆、⑥平行四边形 中是轴对称图形的有 ,是中心对称图形的有 ,既是轴对称图形又是中心对称图形的有 _______
1.下列图形中,是中心对称图形但不是轴对称图形的是( )
练一练
A
①②③④⑤
①④⑤⑥
①④⑤
探究活动三 利用中心对称图形的性质解决问题
一块方角形钢板,如图1所示,如何用一条直线将
其分为面积相等的两部分.
分析:过中心对称图形的对称中心的任意
一条直线都可以把图形分成面积相等的两部分,
本题不是中心对称图形,考虑将其转化。
图1
解法一:(如图2)方角形不是中心对称图形,可以利用分割的方法,将其分成两部分,这两部分都是中心对称图形.这样就可以分别找到这两部分的对称中心,过这两点作一条直线(两点确定一条直线).这条直线既通过点01,又通过点O2,因此直线O1O2(见图2)既将上面的矩形平均分成两部分,又将下面的矩形平均分成两部分,达到了目的,满足了题目的要求.
图2
说明:把一个不是中心对称图形的图形分成面积相等的两部分,其思路是将已知图形分成两个中心对称图形,确定对称中心,过两个对称中心的直线即把图形分割成面积相等的两部分。
解法二:(如图3)、解法三:(如图4).
图3
图4
轴对称
中心对称
有一条对称轴
——直线
有一个对称中心——点
图形沿对称轴翻折后重合
图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分
对称点连线经过对称中心,且被对称中心平分
归纳小结:
类比中心对称与轴对称
【学习目标】
1.通过与轴对称和轴对称图形类比,
理解中心对称和中心对称图形的概念和有关性质;
2.会画一个图形关于某点对称的图形;
3.经历观察、操作、思考、探究中心对称图形的有关概念和基本性质的过程,感受对称、匀称、均衡的美感,积累一定的审美体验。
情境创设
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
探究活动一 探究中心对称的概念及其性质
问题1:上面两张图片中的图形形状、大小相同,如果将其中一个图形绕着某一点旋转1800 ,能与另一个重合吗?
O
A
C
E
F
A
C
O
B
D
把一个图形绕着某一点旋转180°,如果它能够与另外一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成 ,这个点叫做 。
中心对称
对称中心
1.用一张透明纸覆盖在图上,描出四边形ABCD。用大头针钉在点O处,将四边形ABCD绕点O旋转180° ,发现它与四边形A'B'C'D'重合。
四边形ABCD与四边形A'B'C'D'关于点O对称,点O是________,对应点A和A'、B和B'、C和C'、D和D'是关于中心O
的对称点。
做一做:
C'
O
A
B
C
D
A'
B'
D'
问题1:四边形ABCD与四边形A'B'C'D'关于点O成中心对称吗?
对称中心
问题2:分别连接关于点O的对称点A和A'、B和B'、
C和C'、D和D'。你发现了什么?
一个图形绕着某一点旋转180°是一种特殊的旋转。
成中心对称的两个图形具有图形旋转的一切性质。
成中心对称的两个图形,对称点连线都经过___________, 并且被对称中心________。
对称中心
平分
(1)线段AA',BB',CC',DD'相交于点O
(2)OA=OA′、OB=OB′、
OC=OC′、OD=OD′
1. 已知A点和O点,画出点A关于点O的对称点A′
画一画:
A
O
A′
连结AO,
并延长到A′,使OA=OA′,
则A′是所求的点
2.已知线段AB和O点,画出线段AB关于点O的
对称线段A′B′
画一画:
A
A′
B′
B
O
线段A′B′是所求的对称线段
3.已知ΔABC和点0,画ΔA′B′C′,使它与ΔABC关于点0成中心对称。
画一画:
ΔA′B′C′是所求的三角形
A′
C′
B′
C
A
B
O
变式:
1.D是ΔABC的边AC上的一点,
画ΔEFG,使它与ΔABC关于
点D成中心对称。
B
C
A
D
E
F
G
ΔEFG是所求的三角形
2.D是ΔABC内部的一点,画ΔA′B′C′,使它与ΔABC关于点D成中心对称。
变式:
A′
B′
C′
ΔA′B′C′是所求的三角形
3.如图,已知△ABC与△A′B′C′中心对称,请确定其对称中心O。
变式:
A
B
C
A′
B′
C′
O
下列图案有什么共同特征
探究活动二 探究中心对称图形的特征
(1)
(2)
(3)
(4)
旋转图形(1)
旋转图形(2)
旋转图形(3)
旋转图形(4)
旋转
平面内,如果把一个图形绕着某一点旋转180°后能与自身重合,那么这个图形叫做中心对称图形。这个点就是它的对称中心。
探究活动二 探究中心对称图形的特征
中心对称和中心对称图形既有区别又有联系
(1)中心对称图形有一个对称中心,将这个图形绕对称中心旋转180°,旋转后的图形能与原来的图形重合;
(2)中心对称图形是对一个图形来说的,是一个图形所具有的性质;
(3)如果将成中心对称的两个图形看成一个图形,那么这个图形的整体就是中心对称图形;反过来,如果将一个中心对称图形沿过对称中心的任一条直线分成两个图形,那么这两个图形成中心对称.
2.在①线段、②角、 ③等腰三角形、④ 正方形、
⑤圆、⑥平行四边形 中是轴对称图形的有 ,是中心对称图形的有 ,既是轴对称图形又是中心对称图形的有 _______
1.下列图形中,是中心对称图形但不是轴对称图形的是( )
练一练
A
①②③④⑤
①④⑤⑥
①④⑤
探究活动三 利用中心对称图形的性质解决问题
一块方角形钢板,如图1所示,如何用一条直线将
其分为面积相等的两部分.
分析:过中心对称图形的对称中心的任意
一条直线都可以把图形分成面积相等的两部分,
本题不是中心对称图形,考虑将其转化。
图1
解法一:(如图2)方角形不是中心对称图形,可以利用分割的方法,将其分成两部分,这两部分都是中心对称图形.这样就可以分别找到这两部分的对称中心,过这两点作一条直线(两点确定一条直线).这条直线既通过点01,又通过点O2,因此直线O1O2(见图2)既将上面的矩形平均分成两部分,又将下面的矩形平均分成两部分,达到了目的,满足了题目的要求.
图2
说明:把一个不是中心对称图形的图形分成面积相等的两部分,其思路是将已知图形分成两个中心对称图形,确定对称中心,过两个对称中心的直线即把图形分割成面积相等的两部分。
解法二:(如图3)、解法三:(如图4).
图3
图4
轴对称
中心对称
有一条对称轴
——直线
有一个对称中心——点
图形沿对称轴翻折后重合
图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分
对称点连线经过对称中心,且被对称中心平分
归纳小结:
类比中心对称与轴对称
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
