苏科版 七年级数学下册 10.3解二元一次方程组(1) (16张PPT)
文档属性
| 名称 | 苏科版 七年级数学下册 10.3解二元一次方程组(1) (16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览





文档简介
10.3解二元一次方程组
--代入法
1.什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程.
知识回顾
2.把下列方程写成含x的式子表示y的形式.
(1)2x-y=3
(2)3x+y-1=0
解: y=2x-3
解: y=1-3x
知识回顾
像这样,把含有两个未知数的两个一次方程联立
在一起,就组成了一个二元一次方程组.
(1)含有两个未知数
(2)都是一次方程
(3)方程组中同一字母必须代表同一个量
二元一次方程组要点:
10.2二元一次方程组
①
②
解:由①得 y=12-x ③
将③代入②,得2x+12-x=20
解这个一元一次方程,得
x=8
将x=8代入③,得 y=4
所以原方程组的解是
方法练习
用代入法解二元一次方程组的一般步骤
1.变形用一个未知数表示另一个未知数
3.求解解一元一次方程,求解;
把解代入,求另一解;
2.代入将变形后的方程代入另一方程,
得到一个一元一次方程;
4.写答写出方程组的解.
5.检查
1.
所以这个方程组的解为:
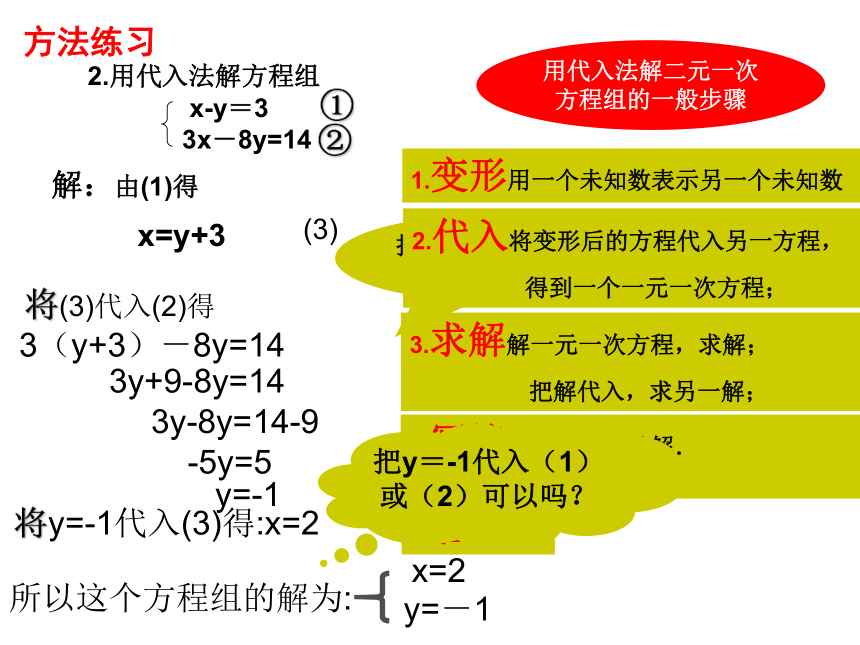
2.用代入法解方程组
x-y=3
3x-8y=14
解:由(1)得
x=y+3
y=-1
将y=-1代入(3)得:x=2
y=-1
x=2
(3)
将(3)代入(2)得
3(y+3)-8y=14
用代入法解二元一次方程组的一般步骤
3y+9-8y=14
3y-8y=14-9
-5y=5
1.变形用一个未知数表示另一个未知数
把(3)代入(1)可以吗?
3.求解解一元一次方程,求解;
把解代入,求另一解;
2.代入将变形后的方程代入另一方程,
得到一个一元一次方程;
4.写答写出方程组的解.
方法练习
①
②
5.检查
把y=-1代入(1)或(2)可以吗?
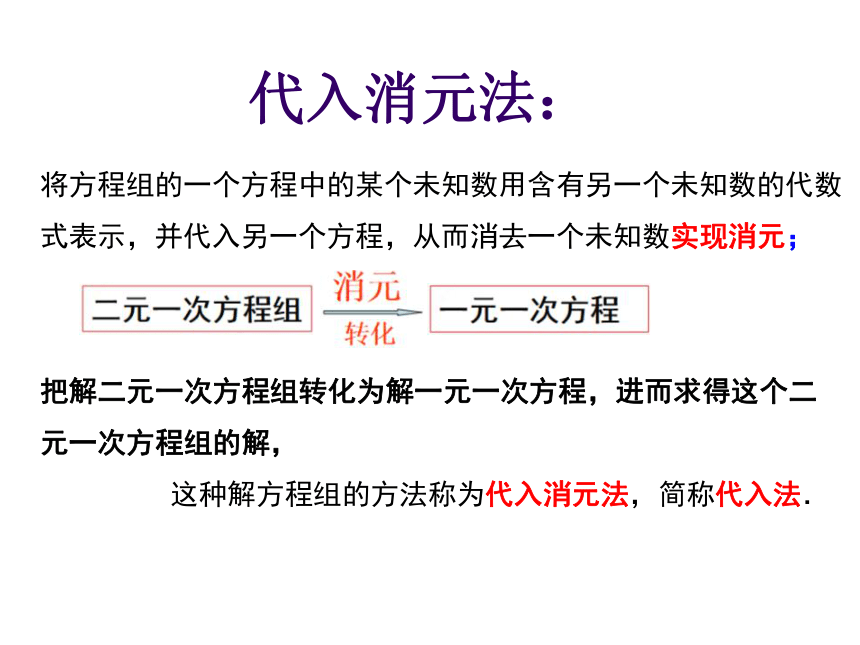
将方程组的一个方程中的某个未知数用含有另一个未知数的代数式表示,并代入另一个方程,从而消去一个未知数实现消元;
把解二元一次方程组转化为解一元一次方程,进而求得这个二元一次方程组的解,
这种解方程组的方法称为代入消元法,简称代入法.
代入消元法:
用代入法解二元一次方程组主要步骤:
1.变形用一个未知数表示另一个未知数
3.求解解一元一次方程,求解;把解代入,求另一解;
2.代入将变形后的方程代入另一方程,得到一个一元一次方程;
4.写答写出方程组的解.
5.检查
练一练
用代入法解下列方程组:
(1)
(2)
(3)
(4)
2x+3y=16 ①
x+4y=13 ②
解:由② ,得 x=13 - 4y ③
将③代入① ,得 2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
将y=2代入③ ,得 x=5
所以原方程组的解是
x=5,
y=2。
1.解方程组
1.变形
3.求解
2.代入
4.写答
巩固练习
5.检查
巩固练习
整体代入
巩固练习
整体代入
巩固练习
5.已知(2x+3y-4)+∣x+3y-7∣=0
则x= ,y= 。
2
-3
—
10
3
巩固练习
归纳总结
将方程组的一个方程中的某个未知数用含有另一个未知数的代数式表示,并代入另一个方程,从而消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为代入消元法,简称为代入法。
1.代入消元法
2.代入法的基本思想:消元.
3.代入法解二元一次方程组主要步骤:
1.变形用一个未知数表示另一个未知数
3.求解解一元一次方程,求解;把解代入,求另一解;
2.代入将变形后的方程代入另一方程,得到一个一元一次方程;
4.写答写出方程组的解.
5.检查
--代入法
1.什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程.
知识回顾
2.把下列方程写成含x的式子表示y的形式.
(1)2x-y=3
(2)3x+y-1=0
解: y=2x-3
解: y=1-3x
知识回顾
像这样,把含有两个未知数的两个一次方程联立
在一起,就组成了一个二元一次方程组.
(1)含有两个未知数
(2)都是一次方程
(3)方程组中同一字母必须代表同一个量
二元一次方程组要点:
10.2二元一次方程组
①
②
解:由①得 y=12-x ③
将③代入②,得2x+12-x=20
解这个一元一次方程,得
x=8
将x=8代入③,得 y=4
所以原方程组的解是
方法练习
用代入法解二元一次方程组的一般步骤
1.变形用一个未知数表示另一个未知数
3.求解解一元一次方程,求解;
把解代入,求另一解;
2.代入将变形后的方程代入另一方程,
得到一个一元一次方程;
4.写答写出方程组的解.
5.检查
1.
所以这个方程组的解为:
2.用代入法解方程组
x-y=3
3x-8y=14
解:由(1)得
x=y+3
y=-1
将y=-1代入(3)得:x=2
y=-1
x=2
(3)
将(3)代入(2)得
3(y+3)-8y=14
用代入法解二元一次方程组的一般步骤
3y+9-8y=14
3y-8y=14-9
-5y=5
1.变形用一个未知数表示另一个未知数
把(3)代入(1)可以吗?
3.求解解一元一次方程,求解;
把解代入,求另一解;
2.代入将变形后的方程代入另一方程,
得到一个一元一次方程;
4.写答写出方程组的解.
方法练习
①
②
5.检查
把y=-1代入(1)或(2)可以吗?
将方程组的一个方程中的某个未知数用含有另一个未知数的代数式表示,并代入另一个方程,从而消去一个未知数实现消元;
把解二元一次方程组转化为解一元一次方程,进而求得这个二元一次方程组的解,
这种解方程组的方法称为代入消元法,简称代入法.
代入消元法:
用代入法解二元一次方程组主要步骤:
1.变形用一个未知数表示另一个未知数
3.求解解一元一次方程,求解;把解代入,求另一解;
2.代入将变形后的方程代入另一方程,得到一个一元一次方程;
4.写答写出方程组的解.
5.检查
练一练
用代入法解下列方程组:
(1)
(2)
(3)
(4)
2x+3y=16 ①
x+4y=13 ②
解:由② ,得 x=13 - 4y ③
将③代入① ,得 2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
将y=2代入③ ,得 x=5
所以原方程组的解是
x=5,
y=2。
1.解方程组
1.变形
3.求解
2.代入
4.写答
巩固练习
5.检查
巩固练习
整体代入
巩固练习
整体代入
巩固练习
5.已知(2x+3y-4)+∣x+3y-7∣=0
则x= ,y= 。
2
-3
—
10
3
巩固练习
归纳总结
将方程组的一个方程中的某个未知数用含有另一个未知数的代数式表示,并代入另一个方程,从而消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为代入消元法,简称为代入法。
1.代入消元法
2.代入法的基本思想:消元.
3.代入法解二元一次方程组主要步骤:
1.变形用一个未知数表示另一个未知数
3.求解解一元一次方程,求解;把解代入,求另一解;
2.代入将变形后的方程代入另一方程,得到一个一元一次方程;
4.写答写出方程组的解.
5.检查
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
