苏科版八年级数学下册9.2:中心对称与中心对称图形 课件(共41张PPT)
文档属性
| 名称 | 苏科版八年级数学下册9.2:中心对称与中心对称图形 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览







文档简介
9.2中心对称与中心对称图形
苏教版八年级下册
数学
情境创设
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
温故知新
在平面内,将图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.
将其中一个图案绕某一定点旋转180°得到另一个图案.
——特殊的旋转
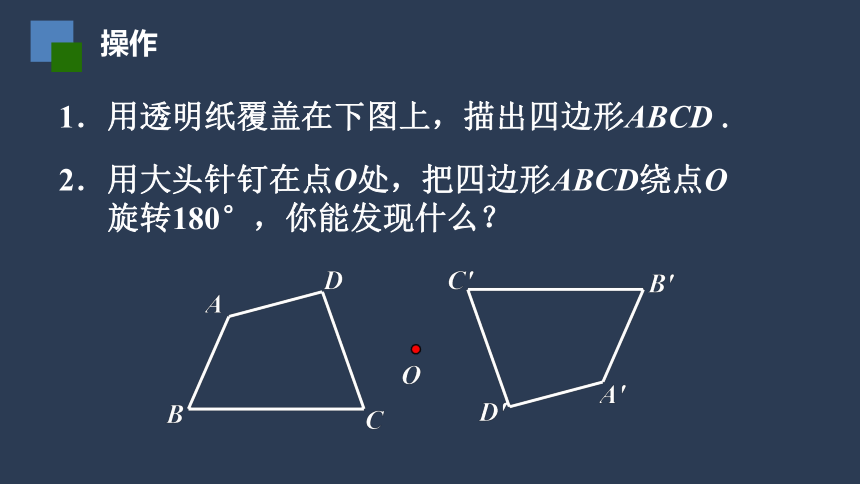
操作
1.用透明纸覆盖在下图上,描出四边形ABCD
.
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
新知
定义:一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么这两个图形关于这点对称,也称这两个图形成中心对称.
这个点叫做对称中心.
如图,四边形ABCD与四边形A′B′C′D′关于点O对称,点O是对称中心.
温故知新
一个图形绕着某一点旋转180°是一种特殊的旋转,成中心对称的两个图形具有图形旋转的一切性质.
1.旋转不改变图形的形状和大小,
即旋转前后图形全等.
2.一个图形和它经过旋转所得到的图形中,
对应点到旋转中心距离相等,两组对应点分
别与旋转中心连线所成的角相等.
探索活动一
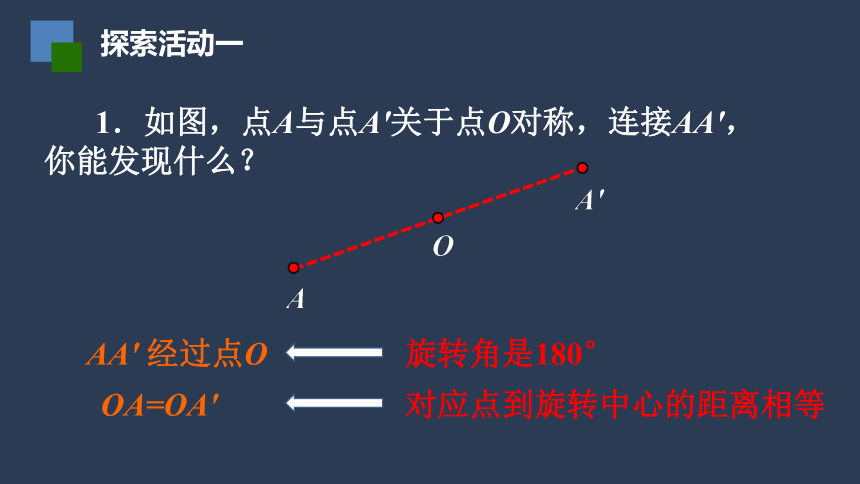
1.如图,点A与点A′关于点O对称,连接AA′,你能发现什么?
AA′
经过点O
OA=OA′
旋转角是180°
对应点到旋转中心的距离相等
探索活动一
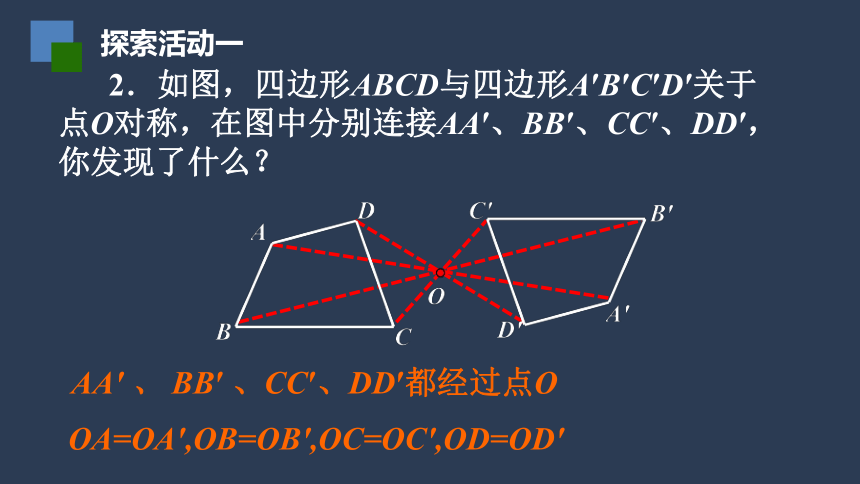
2.如图,四边形ABCD与四边形A′B′C′D′关于点O对称,在图中分别连接AA′、BB′、CC′、DD′,你发现了什么?
AA′
、
BB′
、CC′、DD′都经过点O
OA=OA′,OB=OB′,OC=OC′,OD=OD′
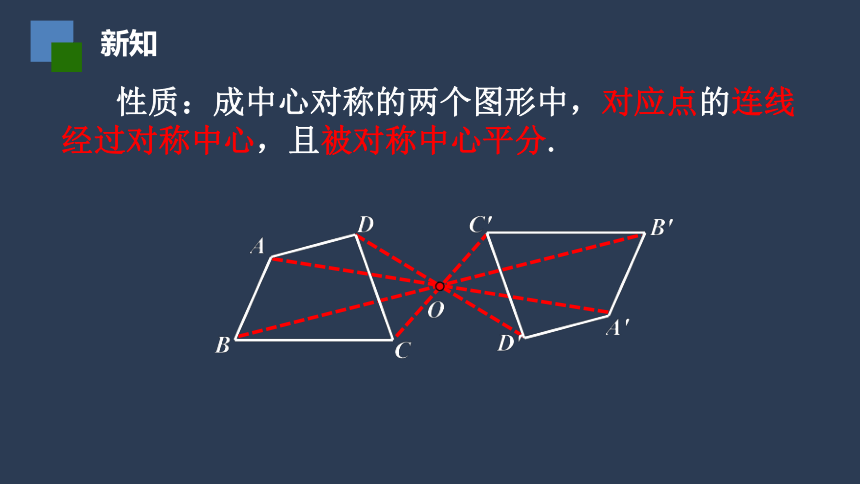
新知
性质:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
探索活动二
1.如图,你能画出点A关于点O对称的点吗?
探索活动二
2.如图,画出线段AB关于点O对称的线段A′B′
.
探索活动二
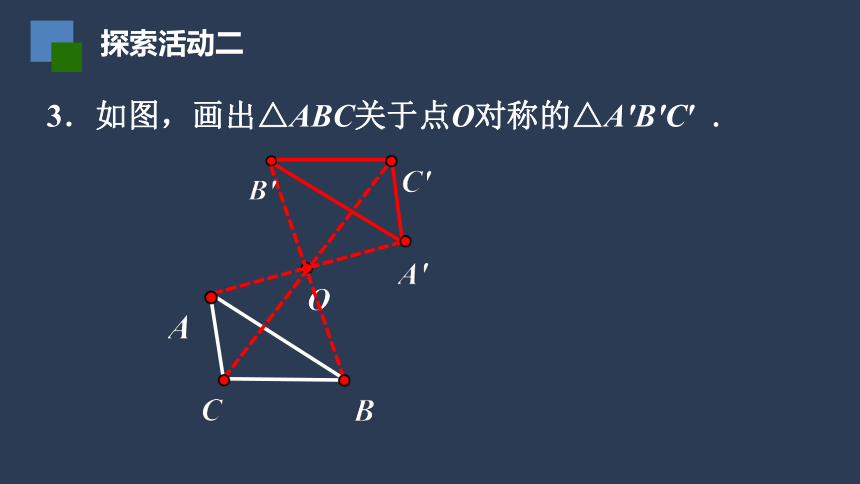
3.如图,画出△ABC关于点O对称的△A′B′C′
.
变式练习
1.如图,画出△ABC关于点A对称的△A′B′C′
.
(A′)
变式练习
2.如图,在△ABC中,点O是AB的中点,画出△ABC关于点O对称的△A′B′C′
.
(A′)
(B′)
3.
如图,已知△ABC与△A′B′C′成中心对称,
画出它们的对称中心O.
变式练习
辨析归纳
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}轴对称
中心对称
有1条对称轴——直线
有1个对称中心——点
一个图形沿对称轴翻折能够与另一个图形重合
一个图形绕对称中心旋转180°能够与另一个图形重合
对应点的连线被对称轴垂直平分
对应点的连线经过对称中心,且被对称中心平分
轴对称与中心对称的联系:都是两个图形按某种规则运动互相重合的特殊的位置关系
拓展提高
如图,直线l1⊥l2,垂足为O,点A1与点A关于直线l1对称,点A2与点A关于直线l2对称,点A1与点A2有怎样的对称关系?你能说明理由吗?
OA=OA1
OA=OA2
OA1
=OA2
∠AOA1
=2∠1
∠AOA2
=2∠2
1
2
∠1+∠2=90°
∠A1OA2
=180°
即A1A2经过点O
对应点的连线都经过某一个点,
且被这个点平分
点A1与点A2关于点O成中心对称
中心对称
性质
定义
画图
判定
轴对称
联系
区别
旋转
特殊
9.2中心对称与中心对称图形(2)
轴对称与中心对称的区别与联系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
轴对称
中心对称
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿一直线对折
(翻折180°)
图形绕一个点旋转180°
共同点
不同点
都是全等变换(完全重合)
都是指两个图形之间的一种特殊的位置关系
9.2中心对称与中心对称图形(2)
(1)
(2)
(3)
(4)
观察下列图案说一说它们有什么共同特征?
9.2中心对称与中心对称图形(2)
旋转
9.2中心对称与中心对称图形(2)
旋
转
9.2中心对称与中心对称图形(2)
旋
转
9.2中心对称与中心对称图形(2)
旋
转
9.2中心对称与中心对称图形(2)
观察下列图案说一说它们有什么共同特征?
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形.
这个点就是它的对称中心.
9.2中心对称与中心对称图形(2)
图片欣赏
感受传统文化,体会对称之美
9.2中心对称与中心对称图形(2)
w
图片欣赏
感受创意设计,体会对称之美
9.2中心对称与中心对称图形(2)
名称
中心对称
中心对称图形
区别
联系
中心对称与中心对称图形有什么区别与联系?
两个图形的
位置关系
具有某种性质的一个图形
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称.
若把成中心对称的两个图形看作一个整体,则成为中心对称图形。
9.2中心对称与中心对称图形(2)
1.下列扑克图案中,是中心对称图形的有____个.
2
辨一辨
9.2中心对称与中心对称图形(2)
2.下列美丽的图案,是中心对称图形的个
数是
(
)
A.
1个
B.
2个
C.
3个
D.
4个
B
辨一辨
9.2中心对称与中心对称图形(2)
3.在26个英文大写正体字母中,哪些字母是中心对称图形?
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
辨一辨
9.2中心对称与中心对称图形(2)
4.在下列图形:①线段、②角、③等边三角形、
④平行四边形、⑤长方形、
⑥正方形
⑦圆中,
中心对称图形有:__________
轴对称图形有:_____________
既是轴对称图形又是中心对称图形的有:______.
①②③⑤⑥⑦
①④⑤⑥⑦
①⑤⑥⑦
辨一辨
9.2中心对称与中心对称图形(2)
①
②
③
④
5.
在方格纸中选择标有序号的一个小正方形涂上颜色,与图中阴影部分构成中心对称图形,应选____.
④
玩一玩
①
②
③
④
9.2中心对称与中心对称图形(2)
6.请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心对称图形,并写上一两句贴切的解说词.
玩一玩
如下图就是符合要求的图形,你能构思其它图形吗?比一比,看谁想得多,看谁想得妙!
9.2中心对称与中心对称图形(2)
7.请你用一条直线将平行四边形分割成面积相等的两部分,
反思:将平行四边形换成其它中心对称图形,刚才的结论还成立吗?
想一想
A
B
C
D
经过对称中心的任意一条直线平分平行四边形的面积
你能画出几条?
9.2中心对称与中心对称图形(2)
变式1:如图,有一块长方形田地,田地内有一口井,现将这块土地平分给两家农户,要求两家合用这口井浇地,请问应如何分?在图中画出分界线.
想一想
9.2中心对称与中心对称图形(2)
变式2:农民张大爷有一块田地如图所示,他想将田分给两个儿子,儿子提出:⑴分割的面积应相等;⑵最好把分割线做成一条水渠,便于灌溉,你能帮助张大爷画出这条分割线吗?
想一想
第9.2中心对称与中心对称图形(2)
变式3:如图四边形OABC是矩形,
若点B的坐标是(8,4),且直线y=kx-3把矩形面积二等分,求k的值及E点的坐标。
O
C
B
A
x
y
E
想一想
分析:易知直线y=kx-3经过对称中心,矩形OABC的对称中心为(4,2)
9.2中心对称与中心对称图形(2)
8、如图,5×5
的正方形点阵中,横纵方向相邻的两点之间的距离都是
1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以
A,B
为
顶点,面积为
2
的阵点平行四边形的个数为
个
9
9.2中心对称与中心对称图形(2)
收获:
1.认识了中心对称图形,学会了如何辨别中心对称图形以及轴对称图形;
2.中心对称图形与中心对称有何区别与联系?
3.感受到了对称之美
9.2中心对称与中心对称图形(2)
数学的对称美是客观世界的一个侧面的反映.哥白尼说:“在这种有条不紊的安排之下,宇宙中存在着奇妙的对称……”.对称是广义的,字母的对称,结构的对称,图形的对称,解法的对称……无论哪种对称,都是美好的.
苏教版八年级下册
数学
情境创设
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
温故知新
在平面内,将图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.
将其中一个图案绕某一定点旋转180°得到另一个图案.
——特殊的旋转
操作
1.用透明纸覆盖在下图上,描出四边形ABCD
.
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
新知
定义:一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么这两个图形关于这点对称,也称这两个图形成中心对称.
这个点叫做对称中心.
如图,四边形ABCD与四边形A′B′C′D′关于点O对称,点O是对称中心.
温故知新
一个图形绕着某一点旋转180°是一种特殊的旋转,成中心对称的两个图形具有图形旋转的一切性质.
1.旋转不改变图形的形状和大小,
即旋转前后图形全等.
2.一个图形和它经过旋转所得到的图形中,
对应点到旋转中心距离相等,两组对应点分
别与旋转中心连线所成的角相等.
探索活动一
1.如图,点A与点A′关于点O对称,连接AA′,你能发现什么?
AA′
经过点O
OA=OA′
旋转角是180°
对应点到旋转中心的距离相等
探索活动一
2.如图,四边形ABCD与四边形A′B′C′D′关于点O对称,在图中分别连接AA′、BB′、CC′、DD′,你发现了什么?
AA′
、
BB′
、CC′、DD′都经过点O
OA=OA′,OB=OB′,OC=OC′,OD=OD′
新知
性质:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
探索活动二
1.如图,你能画出点A关于点O对称的点吗?
探索活动二
2.如图,画出线段AB关于点O对称的线段A′B′
.
探索活动二
3.如图,画出△ABC关于点O对称的△A′B′C′
.
变式练习
1.如图,画出△ABC关于点A对称的△A′B′C′
.
(A′)
变式练习
2.如图,在△ABC中,点O是AB的中点,画出△ABC关于点O对称的△A′B′C′
.
(A′)
(B′)
3.
如图,已知△ABC与△A′B′C′成中心对称,
画出它们的对称中心O.
变式练习
辨析归纳
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}轴对称
中心对称
有1条对称轴——直线
有1个对称中心——点
一个图形沿对称轴翻折能够与另一个图形重合
一个图形绕对称中心旋转180°能够与另一个图形重合
对应点的连线被对称轴垂直平分
对应点的连线经过对称中心,且被对称中心平分
轴对称与中心对称的联系:都是两个图形按某种规则运动互相重合的特殊的位置关系
拓展提高
如图,直线l1⊥l2,垂足为O,点A1与点A关于直线l1对称,点A2与点A关于直线l2对称,点A1与点A2有怎样的对称关系?你能说明理由吗?
OA=OA1
OA=OA2
OA1
=OA2
∠AOA1
=2∠1
∠AOA2
=2∠2
1
2
∠1+∠2=90°
∠A1OA2
=180°
即A1A2经过点O
对应点的连线都经过某一个点,
且被这个点平分
点A1与点A2关于点O成中心对称
中心对称
性质
定义
画图
判定
轴对称
联系
区别
旋转
特殊
9.2中心对称与中心对称图形(2)
轴对称与中心对称的区别与联系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
轴对称
中心对称
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿一直线对折
(翻折180°)
图形绕一个点旋转180°
共同点
不同点
都是全等变换(完全重合)
都是指两个图形之间的一种特殊的位置关系
9.2中心对称与中心对称图形(2)
(1)
(2)
(3)
(4)
观察下列图案说一说它们有什么共同特征?
9.2中心对称与中心对称图形(2)
旋转
9.2中心对称与中心对称图形(2)
旋
转
9.2中心对称与中心对称图形(2)
旋
转
9.2中心对称与中心对称图形(2)
旋
转
9.2中心对称与中心对称图形(2)
观察下列图案说一说它们有什么共同特征?
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形.
这个点就是它的对称中心.
9.2中心对称与中心对称图形(2)
图片欣赏
感受传统文化,体会对称之美
9.2中心对称与中心对称图形(2)
w
图片欣赏
感受创意设计,体会对称之美
9.2中心对称与中心对称图形(2)
名称
中心对称
中心对称图形
区别
联系
中心对称与中心对称图形有什么区别与联系?
两个图形的
位置关系
具有某种性质的一个图形
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称.
若把成中心对称的两个图形看作一个整体,则成为中心对称图形。
9.2中心对称与中心对称图形(2)
1.下列扑克图案中,是中心对称图形的有____个.
2
辨一辨
9.2中心对称与中心对称图形(2)
2.下列美丽的图案,是中心对称图形的个
数是
(
)
A.
1个
B.
2个
C.
3个
D.
4个
B
辨一辨
9.2中心对称与中心对称图形(2)
3.在26个英文大写正体字母中,哪些字母是中心对称图形?
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
辨一辨
9.2中心对称与中心对称图形(2)
4.在下列图形:①线段、②角、③等边三角形、
④平行四边形、⑤长方形、
⑥正方形
⑦圆中,
中心对称图形有:__________
轴对称图形有:_____________
既是轴对称图形又是中心对称图形的有:______.
①②③⑤⑥⑦
①④⑤⑥⑦
①⑤⑥⑦
辨一辨
9.2中心对称与中心对称图形(2)
①
②
③
④
5.
在方格纸中选择标有序号的一个小正方形涂上颜色,与图中阴影部分构成中心对称图形,应选____.
④
玩一玩
①
②
③
④
9.2中心对称与中心对称图形(2)
6.请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心对称图形,并写上一两句贴切的解说词.
玩一玩
如下图就是符合要求的图形,你能构思其它图形吗?比一比,看谁想得多,看谁想得妙!
9.2中心对称与中心对称图形(2)
7.请你用一条直线将平行四边形分割成面积相等的两部分,
反思:将平行四边形换成其它中心对称图形,刚才的结论还成立吗?
想一想
A
B
C
D
经过对称中心的任意一条直线平分平行四边形的面积
你能画出几条?
9.2中心对称与中心对称图形(2)
变式1:如图,有一块长方形田地,田地内有一口井,现将这块土地平分给两家农户,要求两家合用这口井浇地,请问应如何分?在图中画出分界线.
想一想
9.2中心对称与中心对称图形(2)
变式2:农民张大爷有一块田地如图所示,他想将田分给两个儿子,儿子提出:⑴分割的面积应相等;⑵最好把分割线做成一条水渠,便于灌溉,你能帮助张大爷画出这条分割线吗?
想一想
第9.2中心对称与中心对称图形(2)
变式3:如图四边形OABC是矩形,
若点B的坐标是(8,4),且直线y=kx-3把矩形面积二等分,求k的值及E点的坐标。
O
C
B
A
x
y
E
想一想
分析:易知直线y=kx-3经过对称中心,矩形OABC的对称中心为(4,2)
9.2中心对称与中心对称图形(2)
8、如图,5×5
的正方形点阵中,横纵方向相邻的两点之间的距离都是
1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以
A,B
为
顶点,面积为
2
的阵点平行四边形的个数为
个
9
9.2中心对称与中心对称图形(2)
收获:
1.认识了中心对称图形,学会了如何辨别中心对称图形以及轴对称图形;
2.中心对称图形与中心对称有何区别与联系?
3.感受到了对称之美
9.2中心对称与中心对称图形(2)
数学的对称美是客观世界的一个侧面的反映.哥白尼说:“在这种有条不紊的安排之下,宇宙中存在着奇妙的对称……”.对称是广义的,字母的对称,结构的对称,图形的对称,解法的对称……无论哪种对称,都是美好的.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
