苏科版八年级数学下册课件:9.1-图形的旋转(共24张PPT)
文档属性
| 名称 | 苏科版八年级数学下册课件:9.1-图形的旋转(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1021.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览








文档简介
9.1 图形的旋转
八年级(下册)
作 者: 盱眙三中
初中数学
学习目标
1.了解旋转及相关概念,知道图形旋转的性质,能利用性质作图;
2.经历对生活中旋转现象的观察、分析过程,通过具体实例认识旋转.经历对具有旋转特征图形的观察、操作、画图等过程,体会旋转的性质;
3.引导学生用数学的眼光看待生活中的问题,形成用数学的意识以及热爱生活的情感.
.
9.1 图形的旋转
9.1 图形的旋转
9.1 图形的旋转
9.1 图形的旋转
你能再举出生活中类似的例子吗?
9.1 图形的旋转
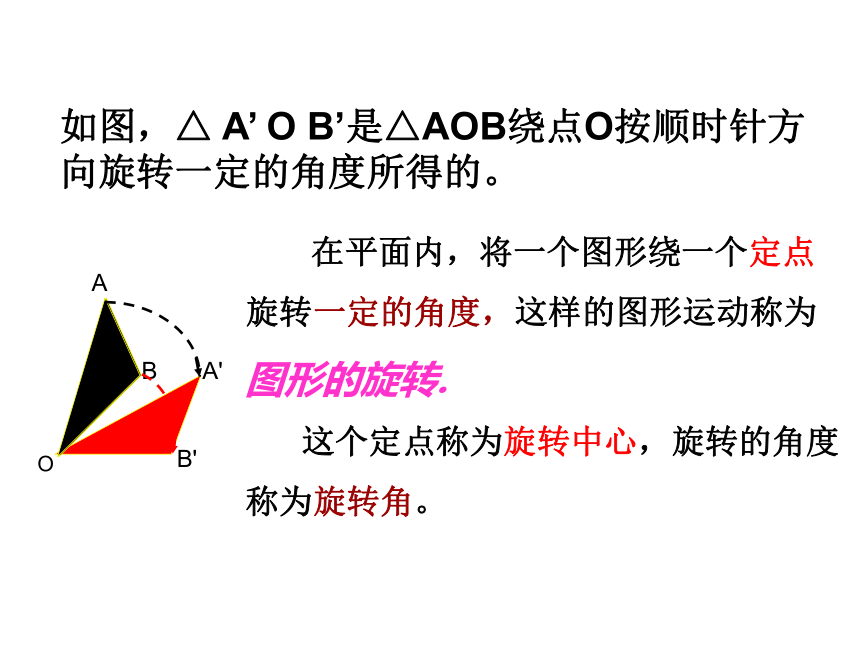
如图,△ A’ O B’是△AOB绕点O按顺时针方向旋转一定的角度所得的。
A'
B'
B
O
A
在平面内,将一个图形绕一个定点
旋转一定的角度,这样的图形运动称为
图形的旋转.
这个定点称为旋转中心,旋转的角度
称为旋转角。
线段AB的对应线段是线段______
∠A的对应角是______
∠B的对应角是______
旋转中心是点______
旋转的角是 ______
线段OB的对应线段是线段______
点B的对应点是点_____
B’
0B’
A’B’
∠A’
∠B’
O
A'
B'
B
O
A
口答
∠AOA’或∠BOB’
1. 将模板放在另一张白纸上,画出三角形,记为△ABC.
2. 用大头针固定点O,将模板绕点O按顺时针方向旋转一定的角度,此时再画出三角形,记为△A ′B ′C ′.
3. 画出各对应点与旋转中心O的连线.
B'
O
A'
C'
B
A
C
探索活动一
9.1 图形的旋转
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
探索活动:
1.操作:
(1)将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.度量∠ACD与∠BCE的度数,线段AC与DC,BC与EC的长度.你发现了什么?
c
E
B
D
A
3.∠ECB=∠DCA;
1.点B和点E对应,点D和点A对应 ;
2.EC=BC,DC=AC;
c
E
B
D
A
(2)将△ABC绕点O按顺时针方向旋转到△A ' B ' C '的位置,度量∠AOA' ∠BOB' ∠COC'的度数,线段AO与AO',BO与BO',CO与CO'的长度.你发现了什么?
2, ∠AOA’=∠BOB’ =∠COC’
1, AO=A’O
BO=B’O
CO=C’O
O
B
C
A
B’
C’
A’
(1)旋转前后的图形全等。即旋转不改变图形的大小、形状。
(2)对应点到旋转中心的距离相等。
(3)每一对对应点与旋转中心的连线所成的角彼此相等,都等于旋转角。
图形旋转的性质:
发现:图形的旋转是由旋转中心和旋转的角度和旋转方向决定.
1.画出将线段AB绕点O按顺时针方向旋转1000后的图形。
O
A
B
1000
C
A'
B'
D
2.操作:
2. 画出将△ABC绕点C按逆时针方向旋转1200后的对应三角形。
A
B
C
B'
A'
1200
如图,△ABC是等边三角形,D是BC上一
点,△ABD经过旋转后到达△ACD’的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
M
D'
C
A
B
D
拓展应用:
下图是由正方形ABCD旋转而成。
(1)旋转中心是__________
(2) 旋转的角度是_________
点A
450
(3) 若正方形的边长是1,则C’D=_________
C'
D'
B'
B
A
C
D
已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,正方形的边长为4,求图中阴影部分的面积.
动脑筋
O
A
B
问题3 如图,已知线段AB绕点O旋转后的对应线段是A′B′,你能确定旋转中心点O的位置吗?
A′
B′
9.1 图形的旋转
A
B
A′
B′
通过本节课的学习,你学到了什么?请谈一谈体会和收获.
课堂小结:
9.1 图形的旋转
八年级(下册)
作 者: 盱眙三中
初中数学
学习目标
1.了解旋转及相关概念,知道图形旋转的性质,能利用性质作图;
2.经历对生活中旋转现象的观察、分析过程,通过具体实例认识旋转.经历对具有旋转特征图形的观察、操作、画图等过程,体会旋转的性质;
3.引导学生用数学的眼光看待生活中的问题,形成用数学的意识以及热爱生活的情感.
.
9.1 图形的旋转
9.1 图形的旋转
9.1 图形的旋转
9.1 图形的旋转
你能再举出生活中类似的例子吗?
9.1 图形的旋转
如图,△ A’ O B’是△AOB绕点O按顺时针方向旋转一定的角度所得的。
A'
B'
B
O
A
在平面内,将一个图形绕一个定点
旋转一定的角度,这样的图形运动称为
图形的旋转.
这个定点称为旋转中心,旋转的角度
称为旋转角。
线段AB的对应线段是线段______
∠A的对应角是______
∠B的对应角是______
旋转中心是点______
旋转的角是 ______
线段OB的对应线段是线段______
点B的对应点是点_____
B’
0B’
A’B’
∠A’
∠B’
O
A'
B'
B
O
A
口答
∠AOA’或∠BOB’
1. 将模板放在另一张白纸上,画出三角形,记为△ABC.
2. 用大头针固定点O,将模板绕点O按顺时针方向旋转一定的角度,此时再画出三角形,记为△A ′B ′C ′.
3. 画出各对应点与旋转中心O的连线.
B'
O
A'
C'
B
A
C
探索活动一
9.1 图形的旋转
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
探索活动:
1.操作:
(1)将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.度量∠ACD与∠BCE的度数,线段AC与DC,BC与EC的长度.你发现了什么?
c
E
B
D
A
3.∠ECB=∠DCA;
1.点B和点E对应,点D和点A对应 ;
2.EC=BC,DC=AC;
c
E
B
D
A
(2)将△ABC绕点O按顺时针方向旋转到△A ' B ' C '的位置,度量∠AOA' ∠BOB' ∠COC'的度数,线段AO与AO',BO与BO',CO与CO'的长度.你发现了什么?
2, ∠AOA’=∠BOB’ =∠COC’
1, AO=A’O
BO=B’O
CO=C’O
O
B
C
A
B’
C’
A’
(1)旋转前后的图形全等。即旋转不改变图形的大小、形状。
(2)对应点到旋转中心的距离相等。
(3)每一对对应点与旋转中心的连线所成的角彼此相等,都等于旋转角。
图形旋转的性质:
发现:图形的旋转是由旋转中心和旋转的角度和旋转方向决定.
1.画出将线段AB绕点O按顺时针方向旋转1000后的图形。
O
A
B
1000
C
A'
B'
D
2.操作:
2. 画出将△ABC绕点C按逆时针方向旋转1200后的对应三角形。
A
B
C
B'
A'
1200
如图,△ABC是等边三角形,D是BC上一
点,△ABD经过旋转后到达△ACD’的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
M
D'
C
A
B
D
拓展应用:
下图是由正方形ABCD旋转而成。
(1)旋转中心是__________
(2) 旋转的角度是_________
点A
450
(3) 若正方形的边长是1,则C’D=_________
C'
D'
B'
B
A
C
D
已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,正方形的边长为4,求图中阴影部分的面积.
动脑筋
O
A
B
问题3 如图,已知线段AB绕点O旋转后的对应线段是A′B′,你能确定旋转中心点O的位置吗?
A′
B′
9.1 图形的旋转
A
B
A′
B′
通过本节课的学习,你学到了什么?请谈一谈体会和收获.
课堂小结:
9.1 图形的旋转
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
