苏科版八年级下册9.2中心对称与中心对称图形课件(30张PPT)
文档属性
| 名称 | 苏科版八年级下册9.2中心对称与中心对称图形课件(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 847.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 14:48:36 | ||
图片预览


文档简介
初二数学:9.2
中心对称与中心对称图形
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
情境创设
C'
O
A
B
C
D
A'
B'
D'
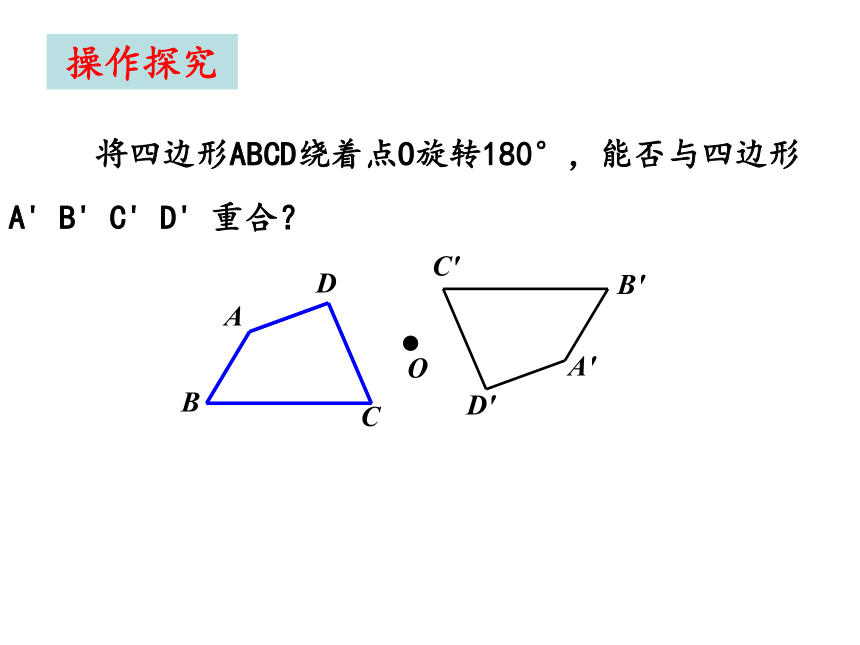
将四边形ABCD绕着点O旋转180°,能否与四边形
A'
B'
C'
D'
重合?
操作探究
C'
O
A
B
C
D
A'
B'
D'
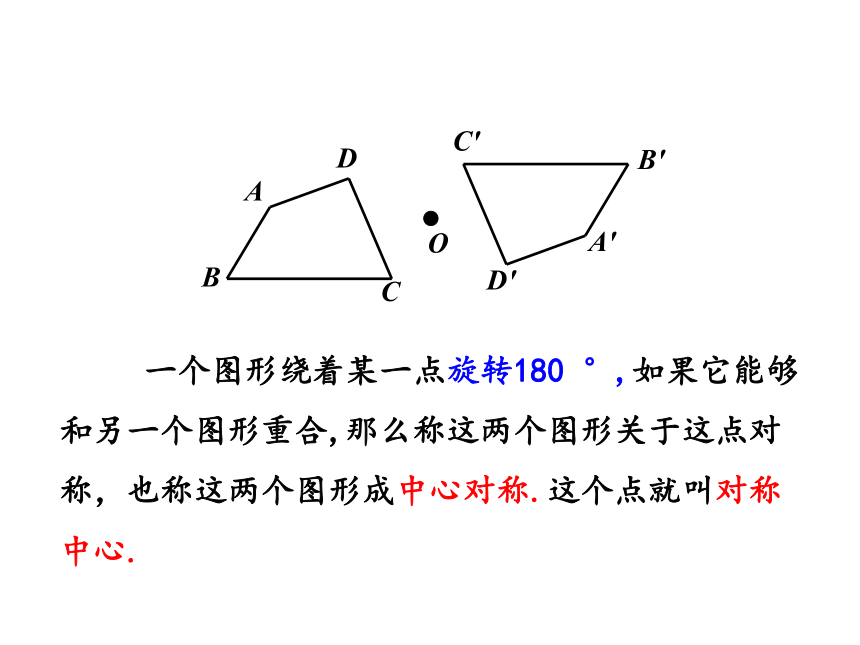
一个图形绕着某一点旋转180
°,如果它能够和另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点就叫对称中心.
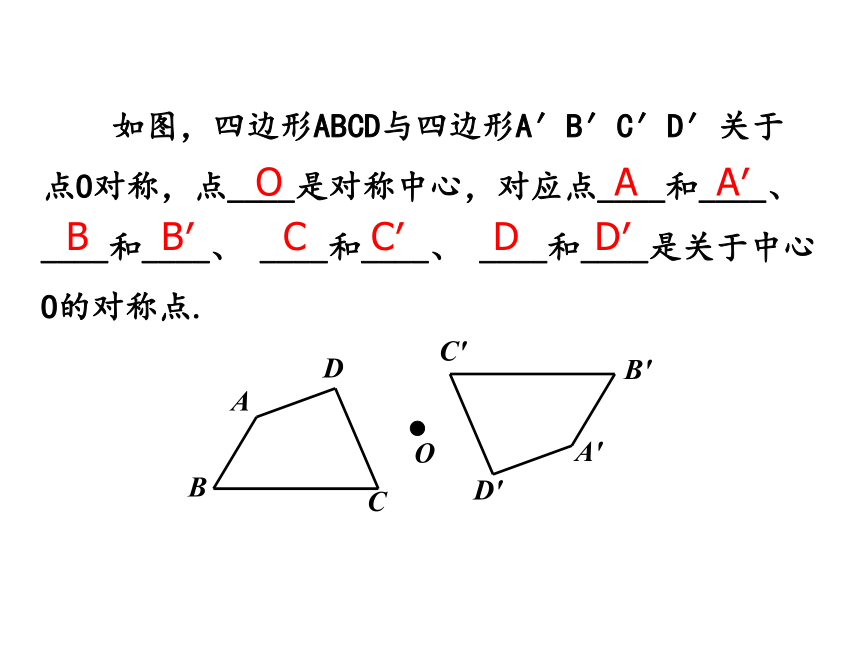
如图,四边形ABCD与四边形A′B′C′D′关于
点O对称,点____是对称中心,对应点____和____、
____和____、
____和____、
____和____是关于中心O的对称点.
O
A
A′
B
C
D
B′
C′
D′
C'
O
A
B
C
D
A'
B'
D'
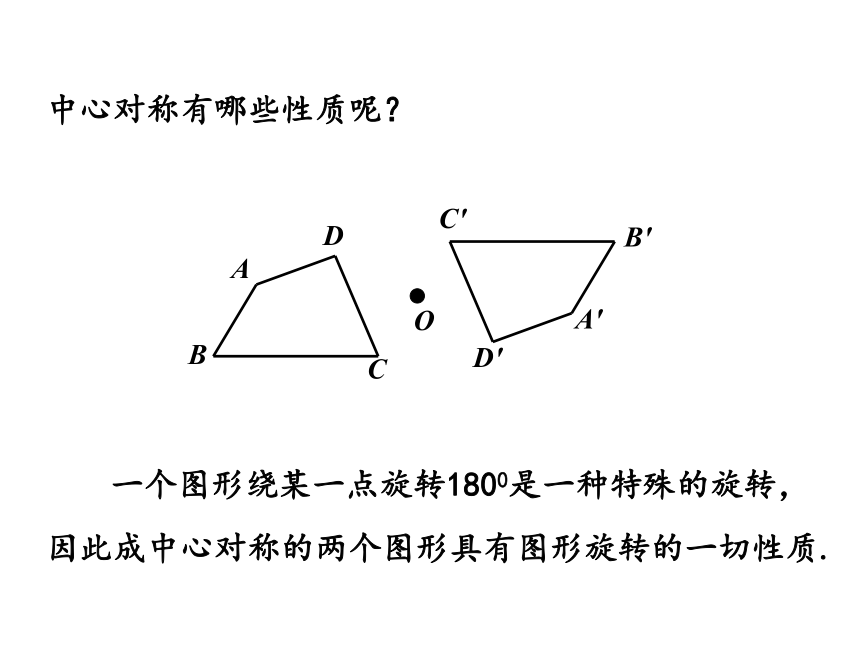
中心对称有哪些性质呢?
C'
O
A
B
C
D
A'
B'
D'
一个图形绕某一点旋转1800是一种特殊的旋转,
因此成中心对称的两个图形具有图形旋转的一切性质.
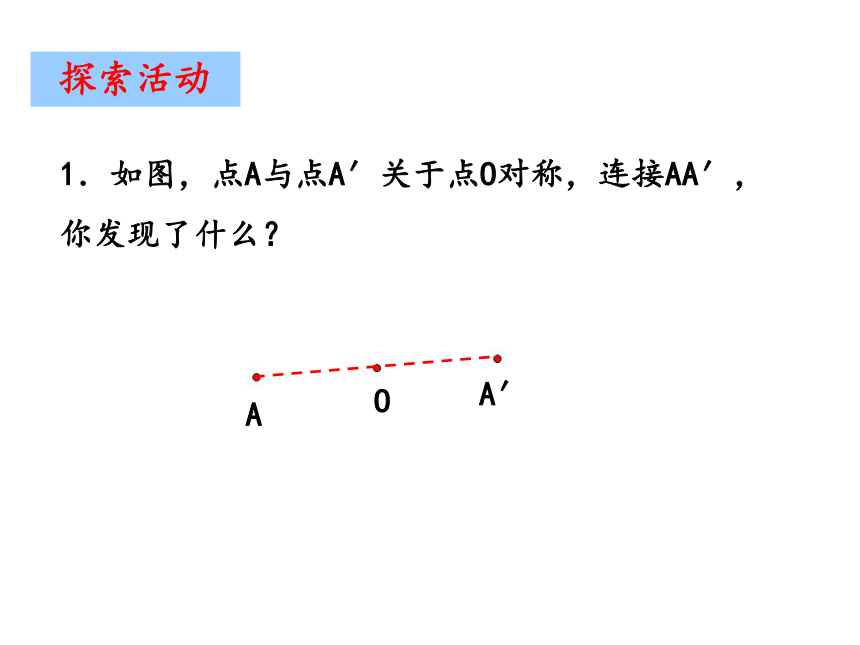
1.如图,点A与点A′关于点O对称,连接AA′,
你发现了什么?
A
A′
O
探索活动
O
A
B
C
D
A'
B'
C'
D'
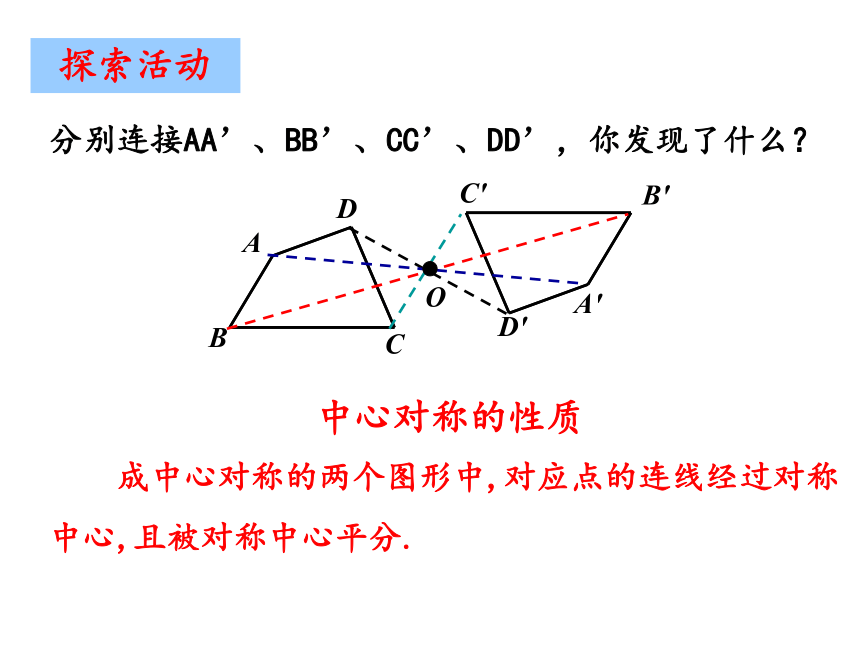
分别连接AA’、BB’、CC’、DD’,你发现了什么?
中心对称的性质
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
探索活动
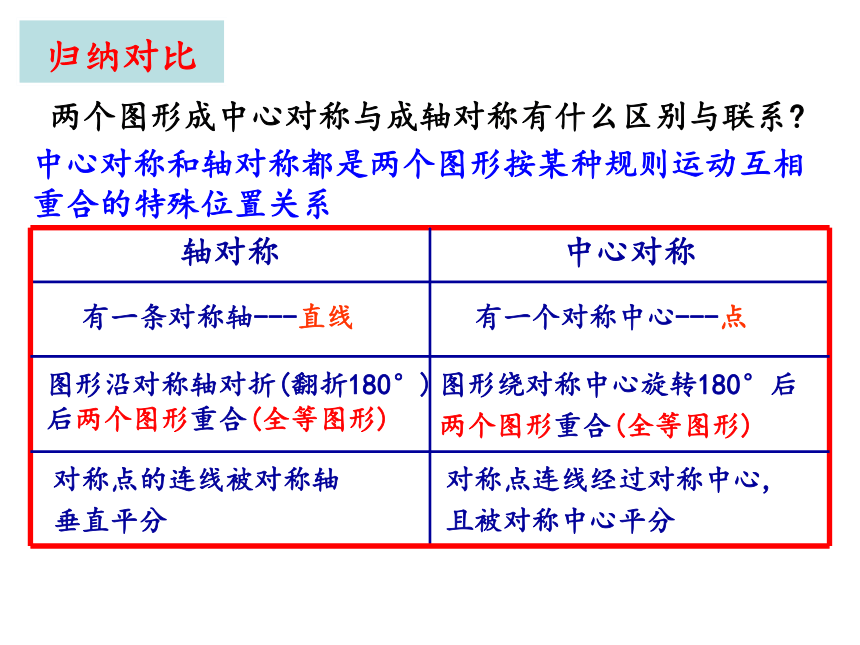
两个图形成中心对称与成轴对称有什么区别与联系?
轴对称
中心对称
有一条对称轴---直线
有一个对称中心---点
图形沿对称轴对折(翻折180°)后两个图形重合(全等图形)
图形绕对称中心旋转180°后
两个图形重合(全等图形)
对称点的连线被对称轴
垂直平分
对称点连线经过对称中心,
且被对称中心平分
归纳对比
中心对称和轴对称都是两个图形按某种规则运动互相重合的特殊位置关系
操作思考
1.如图,已知点A和点O,画出点A关于点O的对称点A′.
A
O
A′
1.连接AO
2.延长AO到点A′,
使OA′=OA
点A′就是点A关于点O的对称点.
2.如图,已知线段AB和点O,画出线段A′B′,使它与
线段AB关于点O成中心对称.
操作思考
O
A
A′
B
B′
线段A′B′就是点A关于点O的对称线段.
操作思考
△
A′B′C′就是△ABC关于点O的对称三角形.
O
A
A′
B
B′
3.如图,已知△ABC和点O,如何画出△
A′B′C′,
使它与△ABC关于点O成中心对称.
C
C′
把一个平面图形绕某一点旋转1800,如果旋转后的
图形能够与原来的图形互相重合,那么这个图形叫做
中心对称图形.这个点就是它的对称中心.
探索讨论
这些图形有什么共同的特征?
知识巩固
1.下图中,哪些是中心对称图形?哪些是轴对称图形?
请画出它们的对称中心或对称轴.
①
②
③
④
⑤
(1)轴对称图形的是
.
(2)中心对称图形的是
.
(3)既是轴对称图形,又是中心对称图形的是
.
①
②
③
④
⑤
①
③
④
①
③
④
中心对称与中心对称图形是两个既有联系又有区别的概念.
区别:中心对称指两个全等图形的相互位置关系,
中心对称图形指一个图形本身成中心对称.
联系:
如果将中心对称图形的两个图形看成一个
整体,则这个整体是中心对称图形.
如果将中心对称图形位于过对称中心的任一条直线两旁的部分看成两个图形,则这两部分成中心对称.
中心对称图形与中心对称的区别和联系?
变式练习:如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°,魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你知道是
( )
A.方块4
B.黑桃5
C.梅花6
D.红桃7
知识巩固
A
2.如图,在△ABC中,O是AC上一点,画△ABC关于点O对称的△A’B’C’.
B
C
A
O
·
·
·
A’
B’
C’
知识巩固
变式练习:如图,等边△ABC的3个顶点都在圆上,请把这个图形补成一个中心对称图形.
知识巩固
解法一:根据观察,B、B’应是对应点,连结BB’,
用刻度尺找出BB’的中点O,则点O即为所求(如图).
A
B
C
A’
B’
C’
O
3.如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O.
知识巩固
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图).
A
B
C
A’
B’
C’
变式练习1:如图,在正方形的4个角上剪去4个相同的小正方形剩余部分是中心对称图形吗?如果是,画出它的对称中心。
知识巩固
O
变式练习2:
如图,已知△ABC以及边AB的中心对称
线段A′B′,先确定对称中心再画出其中心对称三角形.
A
B
C
A′
B′
知识巩固
O
C’
1.如图,直线l1⊥l2,垂足为O,点A1与点A关于直线l1对称,点A2与点A关于直线l2对称,点A1与点A2有怎样的对称关系?你能说明理由吗?
l1
12
A1
A
A2
O
拓展提高
∵点A1与点A关于直线l1对称
∴OA1=OA,∠A1OA=2∠1;
同理:OA2=OA,∠A2OA=2∠2,
∵OA1=OA,OA2=OA,
∴OA1=OA2,
∵∠A1OA=2∠1,∠A2OA=2∠2,
∴∠A1OA+∠A2OA=2(∠1+∠2)
=2×90°=180°,
即点A1、A2的连线经过点O,且OA1=OA2.
解:点A1与点A2关于点O成中心对称.
∴点A1与点A2关于点O成中心对称.
1
2
F
A
D
C
B
E
O
收获反思
1.把一个图形
那么称这两个图形关于这点对称,也称这两个图形
成
,这个点叫做
.
2.成中心对称的两个图形中,
3.中心对称图形:平面内,如果把一个图形绕着某一点
旋转
后能与
,那么这个图形叫做
,这个点就是它的
。
绕着某一点旋转180
°,如果它能够和另一个图形重合,
中心对称
对称中心
对应点的连线经过对称中心,
且被对称中心平分.
对称中心
1800
原来的图形互相重合
中心对称图形
再见
中心对称与中心对称图形
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
情境创设
C'
O
A
B
C
D
A'
B'
D'
将四边形ABCD绕着点O旋转180°,能否与四边形
A'
B'
C'
D'
重合?
操作探究
C'
O
A
B
C
D
A'
B'
D'
一个图形绕着某一点旋转180
°,如果它能够和另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点就叫对称中心.
如图,四边形ABCD与四边形A′B′C′D′关于
点O对称,点____是对称中心,对应点____和____、
____和____、
____和____、
____和____是关于中心O的对称点.
O
A
A′
B
C
D
B′
C′
D′
C'
O
A
B
C
D
A'
B'
D'
中心对称有哪些性质呢?
C'
O
A
B
C
D
A'
B'
D'
一个图形绕某一点旋转1800是一种特殊的旋转,
因此成中心对称的两个图形具有图形旋转的一切性质.
1.如图,点A与点A′关于点O对称,连接AA′,
你发现了什么?
A
A′
O
探索活动
O
A
B
C
D
A'
B'
C'
D'
分别连接AA’、BB’、CC’、DD’,你发现了什么?
中心对称的性质
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
探索活动
两个图形成中心对称与成轴对称有什么区别与联系?
轴对称
中心对称
有一条对称轴---直线
有一个对称中心---点
图形沿对称轴对折(翻折180°)后两个图形重合(全等图形)
图形绕对称中心旋转180°后
两个图形重合(全等图形)
对称点的连线被对称轴
垂直平分
对称点连线经过对称中心,
且被对称中心平分
归纳对比
中心对称和轴对称都是两个图形按某种规则运动互相重合的特殊位置关系
操作思考
1.如图,已知点A和点O,画出点A关于点O的对称点A′.
A
O
A′
1.连接AO
2.延长AO到点A′,
使OA′=OA
点A′就是点A关于点O的对称点.
2.如图,已知线段AB和点O,画出线段A′B′,使它与
线段AB关于点O成中心对称.
操作思考
O
A
A′
B
B′
线段A′B′就是点A关于点O的对称线段.
操作思考
△
A′B′C′就是△ABC关于点O的对称三角形.
O
A
A′
B
B′
3.如图,已知△ABC和点O,如何画出△
A′B′C′,
使它与△ABC关于点O成中心对称.
C
C′
把一个平面图形绕某一点旋转1800,如果旋转后的
图形能够与原来的图形互相重合,那么这个图形叫做
中心对称图形.这个点就是它的对称中心.
探索讨论
这些图形有什么共同的特征?
知识巩固
1.下图中,哪些是中心对称图形?哪些是轴对称图形?
请画出它们的对称中心或对称轴.
①
②
③
④
⑤
(1)轴对称图形的是
.
(2)中心对称图形的是
.
(3)既是轴对称图形,又是中心对称图形的是
.
①
②
③
④
⑤
①
③
④
①
③
④
中心对称与中心对称图形是两个既有联系又有区别的概念.
区别:中心对称指两个全等图形的相互位置关系,
中心对称图形指一个图形本身成中心对称.
联系:
如果将中心对称图形的两个图形看成一个
整体,则这个整体是中心对称图形.
如果将中心对称图形位于过对称中心的任一条直线两旁的部分看成两个图形,则这两部分成中心对称.
中心对称图形与中心对称的区别和联系?
变式练习:如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°,魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你知道是
( )
A.方块4
B.黑桃5
C.梅花6
D.红桃7
知识巩固
A
2.如图,在△ABC中,O是AC上一点,画△ABC关于点O对称的△A’B’C’.
B
C
A
O
·
·
·
A’
B’
C’
知识巩固
变式练习:如图,等边△ABC的3个顶点都在圆上,请把这个图形补成一个中心对称图形.
知识巩固
解法一:根据观察,B、B’应是对应点,连结BB’,
用刻度尺找出BB’的中点O,则点O即为所求(如图).
A
B
C
A’
B’
C’
O
3.如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O.
知识巩固
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图).
A
B
C
A’
B’
C’
变式练习1:如图,在正方形的4个角上剪去4个相同的小正方形剩余部分是中心对称图形吗?如果是,画出它的对称中心。
知识巩固
O
变式练习2:
如图,已知△ABC以及边AB的中心对称
线段A′B′,先确定对称中心再画出其中心对称三角形.
A
B
C
A′
B′
知识巩固
O
C’
1.如图,直线l1⊥l2,垂足为O,点A1与点A关于直线l1对称,点A2与点A关于直线l2对称,点A1与点A2有怎样的对称关系?你能说明理由吗?
l1
12
A1
A
A2
O
拓展提高
∵点A1与点A关于直线l1对称
∴OA1=OA,∠A1OA=2∠1;
同理:OA2=OA,∠A2OA=2∠2,
∵OA1=OA,OA2=OA,
∴OA1=OA2,
∵∠A1OA=2∠1,∠A2OA=2∠2,
∴∠A1OA+∠A2OA=2(∠1+∠2)
=2×90°=180°,
即点A1、A2的连线经过点O,且OA1=OA2.
解:点A1与点A2关于点O成中心对称.
∴点A1与点A2关于点O成中心对称.
1
2
F
A
D
C
B
E
O
收获反思
1.把一个图形
那么称这两个图形关于这点对称,也称这两个图形
成
,这个点叫做
.
2.成中心对称的两个图形中,
3.中心对称图形:平面内,如果把一个图形绕着某一点
旋转
后能与
,那么这个图形叫做
,这个点就是它的
。
绕着某一点旋转180
°,如果它能够和另一个图形重合,
中心对称
对称中心
对应点的连线经过对称中心,
且被对称中心平分.
对称中心
1800
原来的图形互相重合
中心对称图形
再见
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
