苏科版八年级下册9.3 平行四边形(第2课时)课件(共34张PPT)
文档属性
| 名称 | 苏科版八年级下册9.3 平行四边形(第2课时)课件(共34张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 988.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览



文档简介
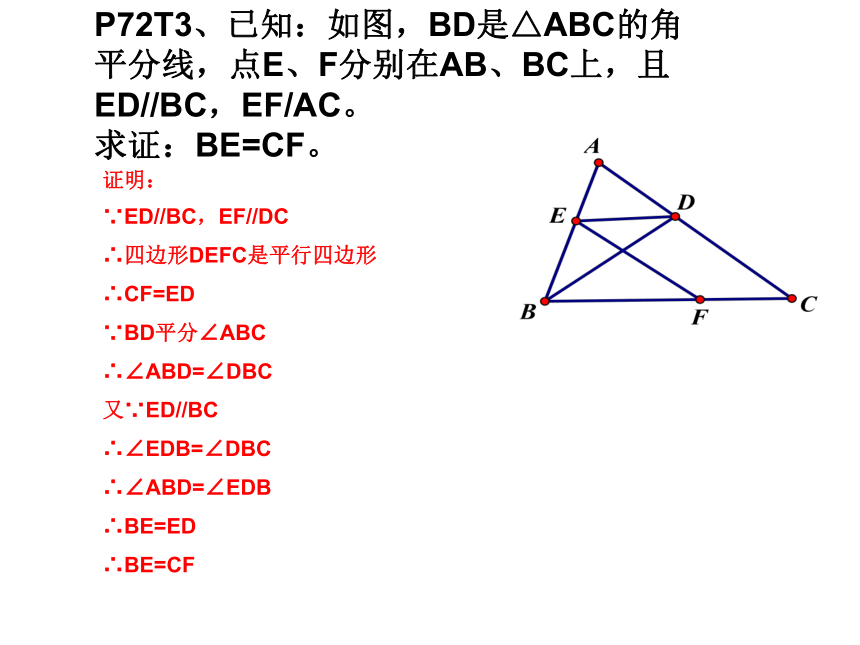
P72T2、已知:如图,在□ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F
求证:BE//DF
作业评析
证明:
∵BE、DF分别平分∠ABC,∠ADC
∴∠EBC=
∠ABC,∠EDF=
∠ADC
∵四边形ABCD是平行四边形
∴∠ABC=∠ADC
∴∠EBC=∠EDF
又∵AD//BC
∴∠AEB=∠EBC
∴∠AEB=∠EDF
∴BE//DF
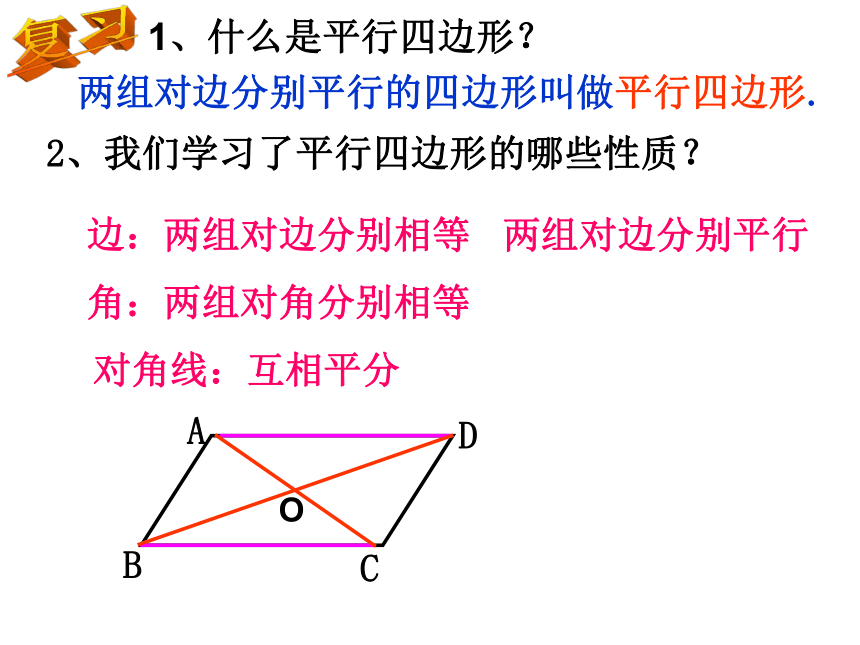
P72T3、已知:如图,BD是△ABC的角平分线,点E、F分别在AB、BC上,且ED//BC,EF/AC。
求证:BE=CF。
证明:
∵ED//BC,EF//DC
∴四边形DEFC是平行四边形
∴CF=ED
∵BD平分∠ABC
∴∠ABD=∠DBC
又∵ED//BC
∴∠EDB=∠DBC
∴∠ABD=∠EDB
∴BE=ED
∴BE=CF
9.3 平行四边形(2)
1.探索并掌握平行四边形的判定条件;
2.能利用平行四边形的判定方法解决有关问题.
重点与难点:
利用平行四边形的判定方法解决有关问题.
学习目标:
A
B
C
D
O
复习
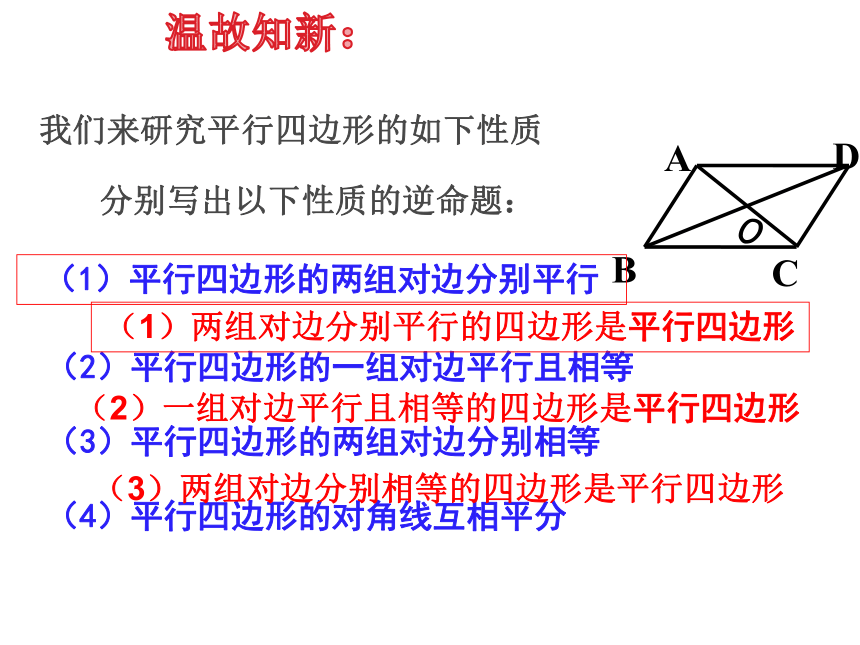
边:两组对边分别相等
两组对边分别平行
角:两组对角分别相等
对角线:互相平分
两组对边分别平行的四边形叫做平行四边形.
2、我们学行四边形的哪些性质?
1、什么是平行四边形?
B
C
A
D
O
温故知新:
(1)平行四边形的两组对边分别平行
(2)平行四边形的一组对边平行且相等
(3)平行四边形的两组对边分别相等
(4)平行四边形的对角线互相平分
分别写出以下性质的逆命题:
(1)两组对边分别平行的四边形是平行四边形
(2)一组对边平行且相等的四边形是平行四边形
我们来研究平行四边形的如下性质
(3)两组对边分别相等的四边形是平行四边形
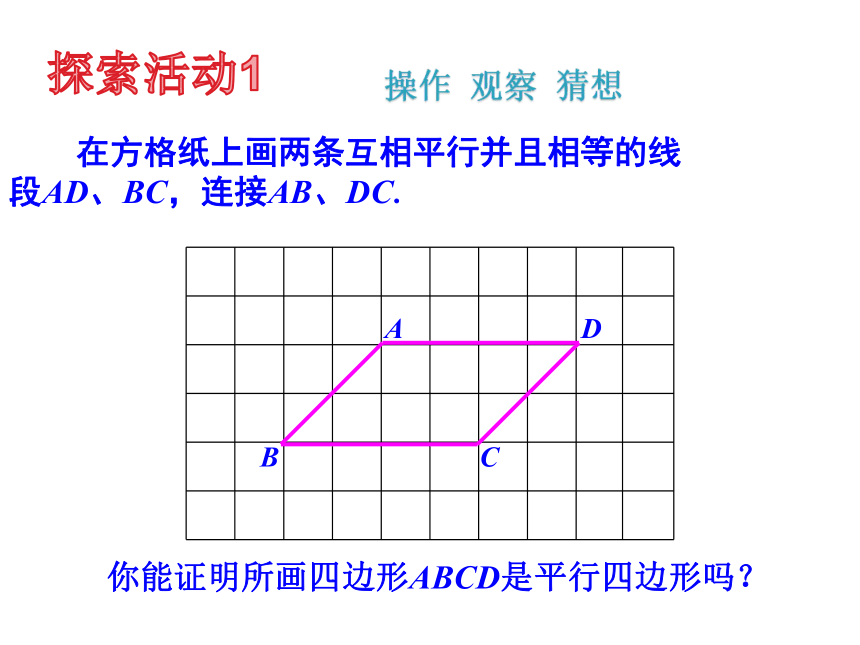
在方格纸上画两条互相平行并且相等的线段AD、BC,连接AB、DC.
探索活动1
你能证明所画四边形ABCD是平行四边形吗?
A
D
B
C
操作
观察
猜想
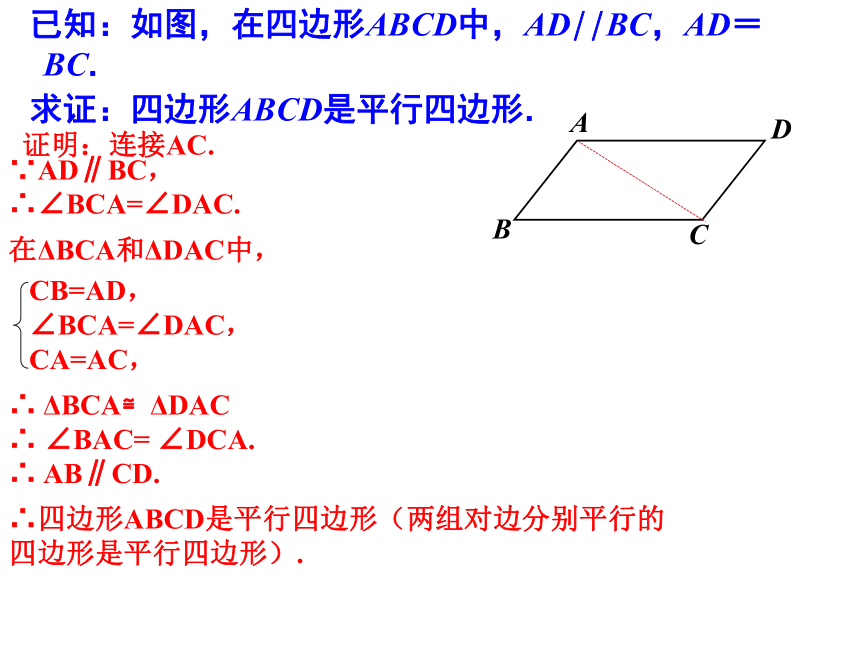
已知:如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形.
B
A
D
C
证明:连接AC.
∵AD∥BC,
∴∠BCA=∠DAC.
在ΔBCA和ΔDAC中,
CB=AD,
∠BCA=∠DAC,
CA=AC,
∴
ΔBCA≌ΔDAC
∴
∠BAC=
∠DCA.
∴
AB∥CD.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
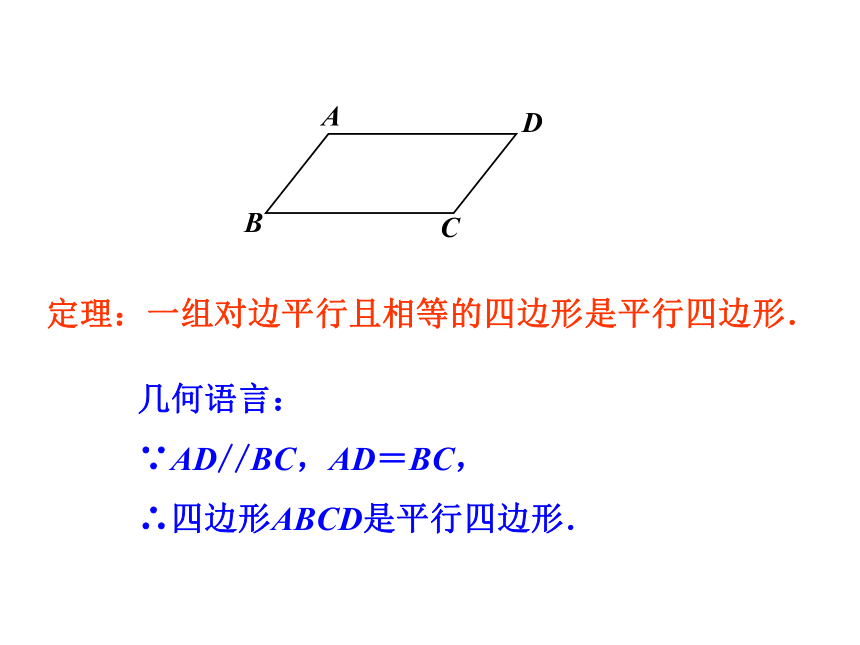
定理:一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
B
A
D
C
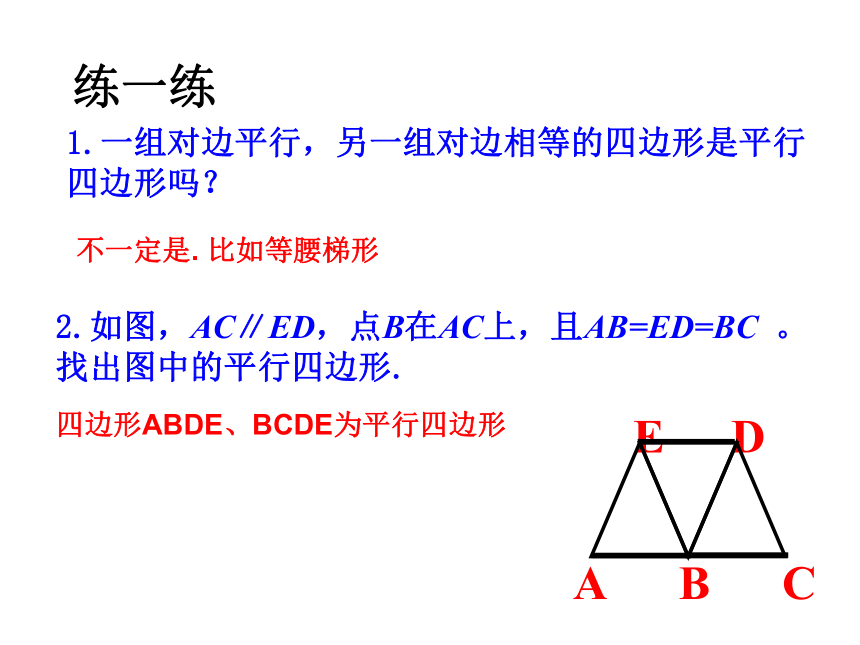
1.一组对边平行,另一组对边相等的四边形是平行
四边形吗?
A
C
B
E
D
2.如图,AC∥ED,点B在AC上,且AB=ED=BC
。
找出图中的平行四边形.
练一练
不一定是.
比如等腰梯形
四边形ABDE、BCDE为平行四边形
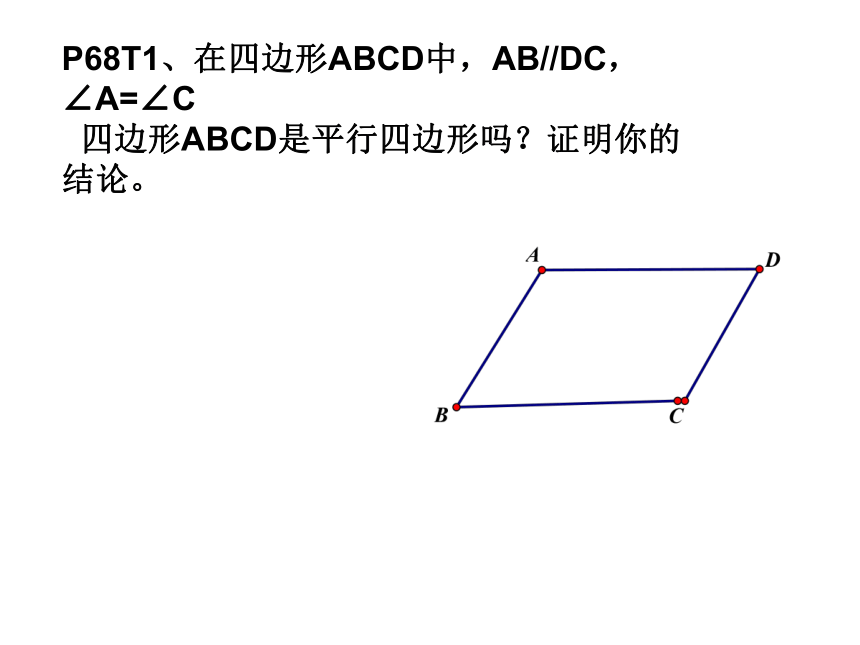
P68T1、在四边形ABCD中,AB//DC,
∠A=∠C
四边形ABCD是平行四边形吗?证明你的结论。
探索活动2
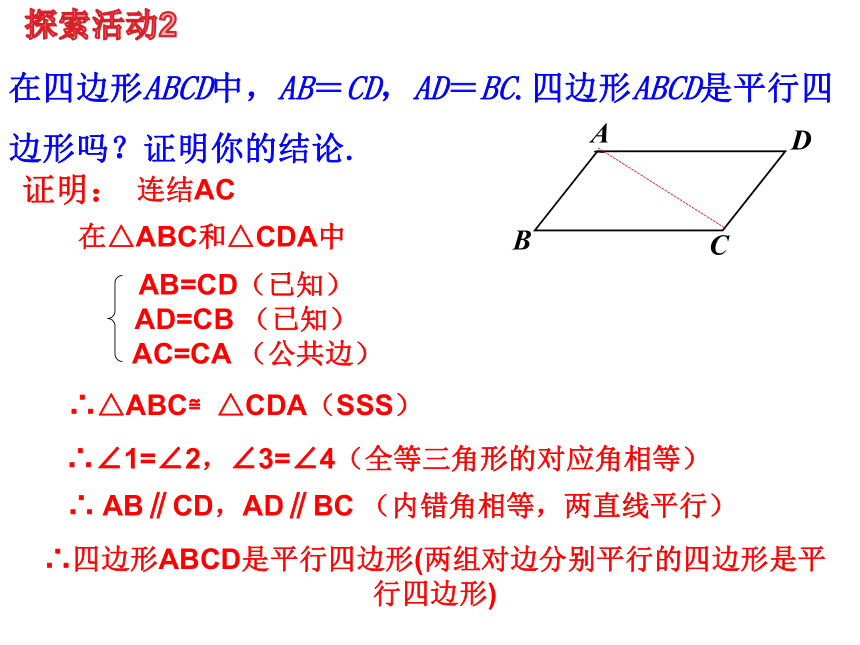
在四边形ABCD中,AB=CD,AD=BC.四边形ABCD是平行四边形吗?证明你的结论.
B
A
D
C
证明:
连结AC
在△ABC和△CDA中
AB=CD(已知)AD=CB
(已知)
AC=CA
(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
定理:两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
B
A
D
C
1.
如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是
。(只填写一个条件,不使用图形以外的字母和线段)
B
A
D
C
练一练
2.
对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
B
A
D
C
练一练
3.两组对边分别相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
2.
一组对边平行且相等的四边形是平行四边形.
判定四边形是平行四边形的依据:
3.判断
(1)一组对边平行且另一组对边相等的四边形是
平行四边形;
(
)
(2)两组对角都相等的四边形是平行四边形
(
)
(3)一组对边平行且一组对角相等的四边形是平行
边形;
(
)
(4)一组对边平行,一组邻角互补的四边形是平行
四边形;
(
)
(5)两组邻角互补的四边形是平行四边形.
(
)
×
√
√
×
×
练一练
新知应用
例1.已知:如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF.
求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC(平行四边形的对边平行且相等).
∵AE=CF,
∴AD-AE=BC-CF,
即
DE=BF.
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形).
已知:如图,在平行四边形ABCD中,点E,F分别在BC、AD上,且BE=DF
求证:AC、EF互相平分
练一练
证明:
连接AE、CF
∵四边形ABCD是平行四边形
∴AD//BC,AD=BC
∵BE=DF
∴BC-BE=AD-DF
即
CE=AF
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴AC与EF互相平分(平行四边形的对角线互相平分)
如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF,AF、BE相交于点G,CE、DF相交于点H.
求证:EF与GH互相平分。
例2
如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
1.已知:如图,在□ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N。
求证:四边形BMDN是平行四边形。
练一练
证明:
∵四边形ABCD是平行四边形
∴∠ABC=∠ADC,AB=DC,AB//CD
又∵BM、DN分别平分∠ABC、∠ADC
∴∠ABM=
∠ADC,∠CDN=
∠ADC
∴∠ABM=∠CDN
又∵AB//CD
∴∠BAM=∠DCN
在△ABM和△CDN中:
∠ABM=∠CDN;
AB=CD;
∠BAM=∠DCN
∴△ABM≌△CDN(ASA)
∴BM=DN,∠AMB=∠CND
∴∠BMN=∠DNM
∴BM//DN
∴四边形BMDN是平行四边形(一组对边平行且相等的四边形是平行四边形)
2.如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF。
求证:四边形BECF是平行四边形。
2.
已知□
ABCD中,E、F分别是对角线AC上的点,且AE=CF.
试猜想线段DE与BF的关系.并证明你的结论.
B
D
C
A
F
E
变1:若将AE=CF变为BE⊥AC,DF⊥AC,其它条件不变,原题的结论还成立吗?请证明.
B
D
C
A
F
E
如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD。求证:四边形ABED是平行四边形。
拓展延伸
如图,在四边形ABCD中,AB=CD=13,AD=5,AC⊥BC,AC⊥AD,试判断四边形ABCD的形状,并说明理由
如图,四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F
求证:四边形ABCD是平行四边形。
已知□
ABCD中,E、F分别是对角线AC上的点,且AE=CF.
试猜想线段DE与BF的关系.并证明你的结论.
B
D
C
A
F
E
能力提升
在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,几秒后四边形ABQP是平行四边形?
感悟与收获
这节课学习了什么?
有什么收获?
A
B
C
D
O
归纳
两组对边分别平行的四边形是平行四边形(定义);
一组对边平行且相等的四边形是平行四边形;
AD∥BC
AB∥DC
AD=BC
AB=DC
AD∥BC
AD=BC
四边形ABCD是平行四边形
如图,用符号表示如下:
我们已经学行四边形的哪些判定方法?
两组对边分别相等的四边形是平行四边形;
四边形ABCD是平行四边形
四边形ABCD是平行四边形
作业
课本
第68页练习1、2、3
第72页习题9.3 第
5
、
6
题
求证:BE//DF
作业评析
证明:
∵BE、DF分别平分∠ABC,∠ADC
∴∠EBC=
∠ABC,∠EDF=
∠ADC
∵四边形ABCD是平行四边形
∴∠ABC=∠ADC
∴∠EBC=∠EDF
又∵AD//BC
∴∠AEB=∠EBC
∴∠AEB=∠EDF
∴BE//DF
P72T3、已知:如图,BD是△ABC的角平分线,点E、F分别在AB、BC上,且ED//BC,EF/AC。
求证:BE=CF。
证明:
∵ED//BC,EF//DC
∴四边形DEFC是平行四边形
∴CF=ED
∵BD平分∠ABC
∴∠ABD=∠DBC
又∵ED//BC
∴∠EDB=∠DBC
∴∠ABD=∠EDB
∴BE=ED
∴BE=CF
9.3 平行四边形(2)
1.探索并掌握平行四边形的判定条件;
2.能利用平行四边形的判定方法解决有关问题.
重点与难点:
利用平行四边形的判定方法解决有关问题.
学习目标:
A
B
C
D
O
复习
边:两组对边分别相等
两组对边分别平行
角:两组对角分别相等
对角线:互相平分
两组对边分别平行的四边形叫做平行四边形.
2、我们学行四边形的哪些性质?
1、什么是平行四边形?
B
C
A
D
O
温故知新:
(1)平行四边形的两组对边分别平行
(2)平行四边形的一组对边平行且相等
(3)平行四边形的两组对边分别相等
(4)平行四边形的对角线互相平分
分别写出以下性质的逆命题:
(1)两组对边分别平行的四边形是平行四边形
(2)一组对边平行且相等的四边形是平行四边形
我们来研究平行四边形的如下性质
(3)两组对边分别相等的四边形是平行四边形
在方格纸上画两条互相平行并且相等的线段AD、BC,连接AB、DC.
探索活动1
你能证明所画四边形ABCD是平行四边形吗?
A
D
B
C
操作
观察
猜想
已知:如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形.
B
A
D
C
证明:连接AC.
∵AD∥BC,
∴∠BCA=∠DAC.
在ΔBCA和ΔDAC中,
CB=AD,
∠BCA=∠DAC,
CA=AC,
∴
ΔBCA≌ΔDAC
∴
∠BAC=
∠DCA.
∴
AB∥CD.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
定理:一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
B
A
D
C
1.一组对边平行,另一组对边相等的四边形是平行
四边形吗?
A
C
B
E
D
2.如图,AC∥ED,点B在AC上,且AB=ED=BC
。
找出图中的平行四边形.
练一练
不一定是.
比如等腰梯形
四边形ABDE、BCDE为平行四边形
P68T1、在四边形ABCD中,AB//DC,
∠A=∠C
四边形ABCD是平行四边形吗?证明你的结论。
探索活动2
在四边形ABCD中,AB=CD,AD=BC.四边形ABCD是平行四边形吗?证明你的结论.
B
A
D
C
证明:
连结AC
在△ABC和△CDA中
AB=CD(已知)AD=CB
(已知)
AC=CA
(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
定理:两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
B
A
D
C
1.
如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是
。(只填写一个条件,不使用图形以外的字母和线段)
B
A
D
C
练一练
2.
对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
B
A
D
C
练一练
3.两组对边分别相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
2.
一组对边平行且相等的四边形是平行四边形.
判定四边形是平行四边形的依据:
3.判断
(1)一组对边平行且另一组对边相等的四边形是
平行四边形;
(
)
(2)两组对角都相等的四边形是平行四边形
(
)
(3)一组对边平行且一组对角相等的四边形是平行
边形;
(
)
(4)一组对边平行,一组邻角互补的四边形是平行
四边形;
(
)
(5)两组邻角互补的四边形是平行四边形.
(
)
×
√
√
×
×
练一练
新知应用
例1.已知:如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF.
求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC(平行四边形的对边平行且相等).
∵AE=CF,
∴AD-AE=BC-CF,
即
DE=BF.
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形).
已知:如图,在平行四边形ABCD中,点E,F分别在BC、AD上,且BE=DF
求证:AC、EF互相平分
练一练
证明:
连接AE、CF
∵四边形ABCD是平行四边形
∴AD//BC,AD=BC
∵BE=DF
∴BC-BE=AD-DF
即
CE=AF
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴AC与EF互相平分(平行四边形的对角线互相平分)
如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF,AF、BE相交于点G,CE、DF相交于点H.
求证:EF与GH互相平分。
例2
如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
1.已知:如图,在□ABCD中,∠ABC、∠ADC的平分线分别交对角线AC于点M、N。
求证:四边形BMDN是平行四边形。
练一练
证明:
∵四边形ABCD是平行四边形
∴∠ABC=∠ADC,AB=DC,AB//CD
又∵BM、DN分别平分∠ABC、∠ADC
∴∠ABM=
∠ADC,∠CDN=
∠ADC
∴∠ABM=∠CDN
又∵AB//CD
∴∠BAM=∠DCN
在△ABM和△CDN中:
∠ABM=∠CDN;
AB=CD;
∠BAM=∠DCN
∴△ABM≌△CDN(ASA)
∴BM=DN,∠AMB=∠CND
∴∠BMN=∠DNM
∴BM//DN
∴四边形BMDN是平行四边形(一组对边平行且相等的四边形是平行四边形)
2.如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF。
求证:四边形BECF是平行四边形。
2.
已知□
ABCD中,E、F分别是对角线AC上的点,且AE=CF.
试猜想线段DE与BF的关系.并证明你的结论.
B
D
C
A
F
E
变1:若将AE=CF变为BE⊥AC,DF⊥AC,其它条件不变,原题的结论还成立吗?请证明.
B
D
C
A
F
E
如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD。求证:四边形ABED是平行四边形。
拓展延伸
如图,在四边形ABCD中,AB=CD=13,AD=5,AC⊥BC,AC⊥AD,试判断四边形ABCD的形状,并说明理由
如图,四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F
求证:四边形ABCD是平行四边形。
已知□
ABCD中,E、F分别是对角线AC上的点,且AE=CF.
试猜想线段DE与BF的关系.并证明你的结论.
B
D
C
A
F
E
能力提升
在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,几秒后四边形ABQP是平行四边形?
感悟与收获
这节课学习了什么?
有什么收获?
A
B
C
D
O
归纳
两组对边分别平行的四边形是平行四边形(定义);
一组对边平行且相等的四边形是平行四边形;
AD∥BC
AB∥DC
AD=BC
AB=DC
AD∥BC
AD=BC
四边形ABCD是平行四边形
如图,用符号表示如下:
我们已经学行四边形的哪些判定方法?
两组对边分别相等的四边形是平行四边形;
四边形ABCD是平行四边形
四边形ABCD是平行四边形
作业
课本
第68页练习1、2、3
第72页习题9.3 第
5
、
6
题
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
