苏科版七年级数学下册7.2: 探索平行线的性质 课件(共26张PPT)
文档属性
| 名称 | 苏科版七年级数学下册7.2: 探索平行线的性质 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 966.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 09:08:29 | ||
图片预览



文档简介
7.2 探索平行线的性质
复习回顾
1
A
B
C
D
M
N
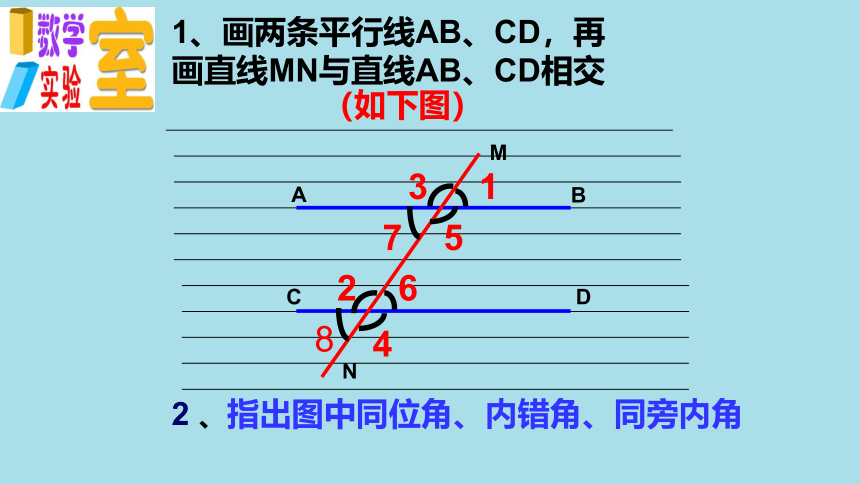
1、画两条平行线AB、CD,再画直线MN与直线AB、CD相交
2 、指出图中同位角、内错角、同旁内角
1
3
6
8
2
5
7
4
(如下图)
( )
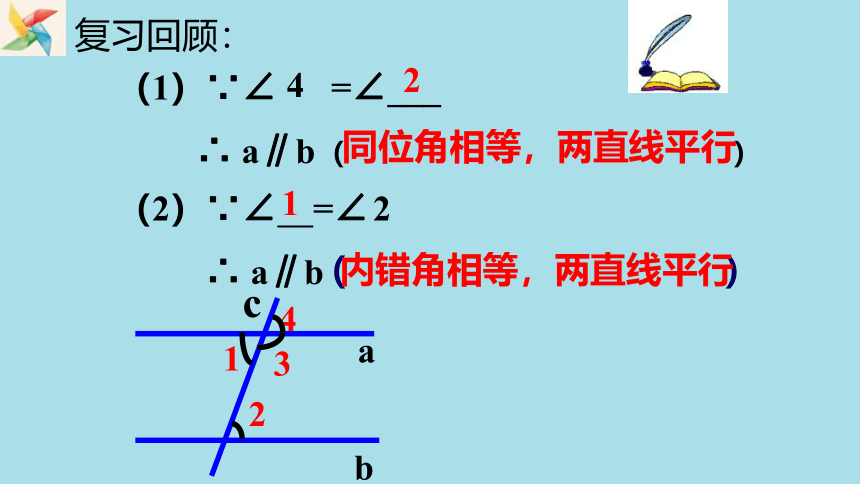
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
1
2
2
4
同位角相等,两直线平行
内错角相等,两直线平行
c
b
4
3
2
1
a
复习回顾:
( )
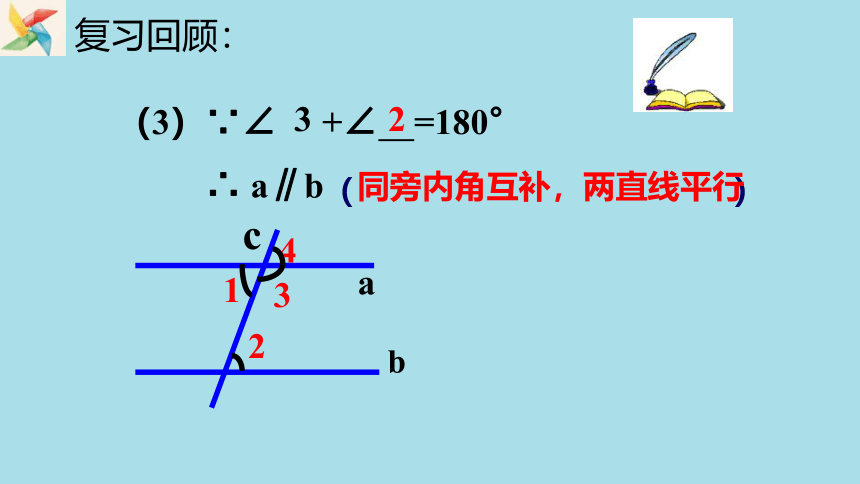
(3)∵∠ +∠ =180°
∴ a∥b
2
3
同旁内角互补,两直线平行
4
3
2
1
a
c
b
复习回顾:
探索新知
2
7
2
5
6
3
1
8
4
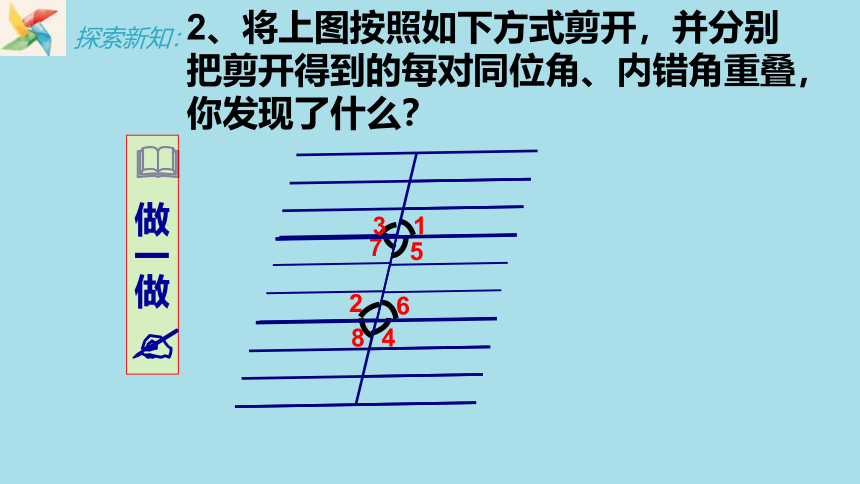
2、将上图按照如下方式剪开,并分别把剪开得到的每对同位角、内错角重叠,你发现了什么?
?
做一做
?
探索新知:
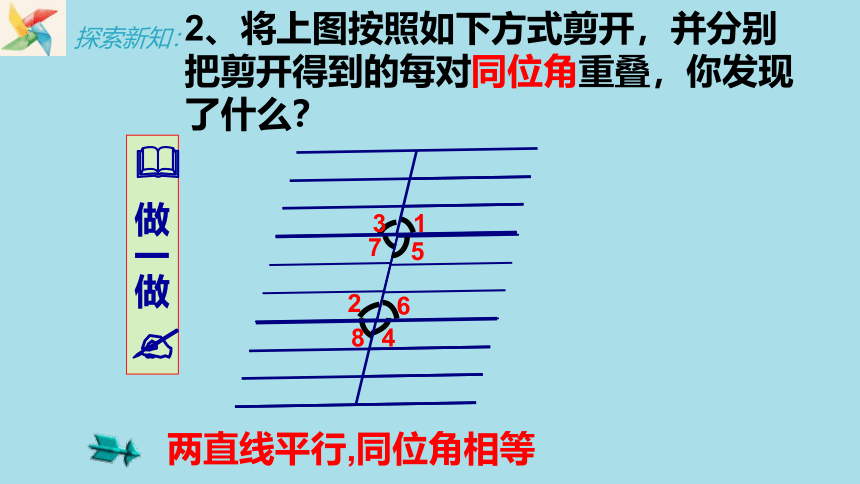
2、将上图按照如下方式剪开,并分别把剪开得到的每对同位角重叠,你发现了什么?
?
做一做
?
7
2
5
6
两直线平行,同位角相等
3
1
8
4
探索新知:
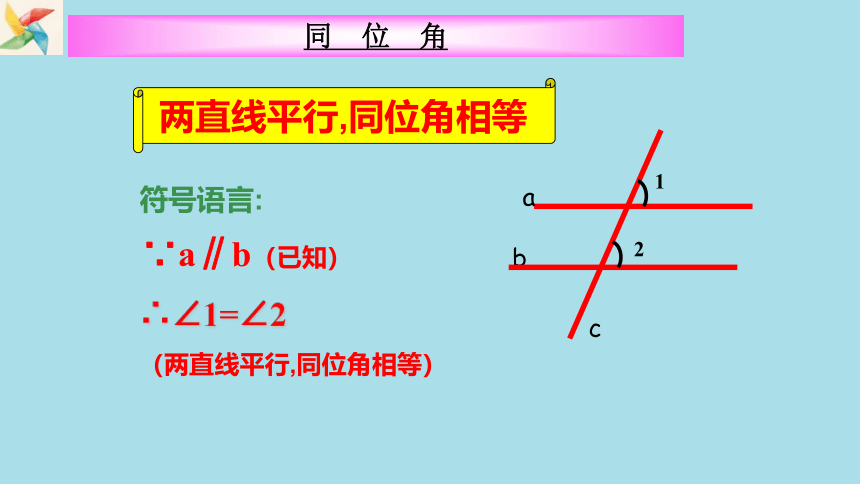
两直线平行,同位角相等
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
符号语言:
b
1
2
a
c
同 位 角
2、将上图按照如下方式剪开,并分别把剪开得到的每对 重叠,你发现了什么?
?
做一做
?
8
4
7
2
5
6
3
1
两直线平行,内错角相等
内错角
探索新知:
两直线平行,内错角相等
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
符号语言:
b
1
2
a
c
3
内 错 角
你能根据”两直线平行,同位角相等”,说明“两直线平行,内错角相等”成立的理由吗?
a
b
c
1
2
3
解:
∵a∥b
∴∠1=∠2
如图所示
又∵ ∠1=∠3
(对顶角相等)
(已知)
(两直线平行,同位角相等)
∴∠2=∠3
(等量代换)
?
做一做
?
7
2
5
6
3、将图中的每对同旁内角剪成两部分,并把他们拼到一起去,你发现每对同旁内角之间有什么关系?
两直线平行,同旁内角互补.
7
3
1
8
4
2
探索新知:
两直线平行,同旁内角互补
∴∠2+∠3=180°
(两直线平行,同旁内角互补)
∵a∥b(已知)
符号语言:
a
3
2
b
同 旁 内 角
如果我们现在只知道“两直线平行,同位角相等”.你能说明“两直线平行,同旁内角互补”成立的理由吗?
∴ ∠2 + ∠3 = 180°
解:
如图所示
1
a
3
2
b
∵a∥b
(已知)
∴∠1=∠2
(两直线平行,同位角相等)
又∵ ∠1+∠3 = 180°
(平角定义)
(等量代换)
例题讲解
3
例1: 如图,已知直线a∥b,∠1 = 500,求∠2的度数.
a
b
c
1
2
∴∠ 2= 500 (等量代换).
解:∵ a∥b (已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
例题讲解:
A
B
C
D
2
1
例2: 如图:已知AB∥CD,求
∠A+∠B+∠ACB的度数.
解:∵AB∥CD(已知)
∴∠A=∠1(两直线平行,内错角相等)
∵ AB∥CD (已知)
∴∠B=∠2(两直线平行,同位角相等)
∴∠ A+∠B+∠ACB
= ∠1+ ∠2+ ∠ACB= 180°
例题讲解:
例3 :如图,AD∥BC, ∠A=∠C.
试说明AB∥DC
A
E
F
C
B
D
(同位角相等,两直线平行)
解:
∵AD∥BC(已知)
∴∠C=∠CDE
(两直线平行,内错角相等)
又∵ ∠A=∠C(已知)
∴ ∠A=∠CDE
(等量代换)
∴AB∥DC
例题讲解:
1.如图,若AB ∥ CD,则下列结论中
① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B
④ ∠B + ∠BCD= 180°正确的是 ( )
A ① ② B ① ③
C ① ④ D ③ ④
D
A
B
E
C
D
1
2
3
×
√
×
√
课堂反馈:
2.如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?
1420
B
C
A
D
?
解:
∵AB∥CD (已知),
∴∠B=∠C
(两直线平行,内错角相等).
又∵∠B=142° (已知),
∴∠B=∠C=142°
(等量代换).
课堂反馈:
3.如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数?
A
B
C
D
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800
(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).
②根据题目的已知条件,
无法求出∠A的度数.
课堂反馈:
4.如图,若AB ∥ ED,BC ∥ FE,则∠B + ∠E=_______
A
B
C
D
E
F
°
180
课堂反馈:
解:∵AB∥DE (已知)
∴∠B=∠BCE
(两直线平行,内错角相等)
∵BC∥FE(已知)
∴∠BCE+∠E=180?
(两直线平行,同旁内角互补)
∴∠B+∠E=180?(等量代换)
5.已知:如图,AB∥CD,∠1=∠2,
则GP与QH的位置关系是什么?并说明理由.
课堂反馈:
解:GP∥QH.
理由如下:
∵AB∥CD,
∴∠EGB=∠EHD.(两直线平行,同位角相等)
又∵∠1=∠2,∠EGP=∠EGB-∠1,∠EHQ=∠EHD-∠2,
∴∠EGP=∠EHQ,(等式的性质)
∴GP∥HQ.(同位角相等,两直线平行)
课堂小结
4
课堂小结:
通过本节课的学习,你有什么感悟?
(1)平行线的三条性质
(2)利用平行线的三条性质解计算题和简单
的解答题
复习回顾
1
A
B
C
D
M
N
1、画两条平行线AB、CD,再画直线MN与直线AB、CD相交
2 、指出图中同位角、内错角、同旁内角
1
3
6
8
2
5
7
4
(如下图)
( )
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
1
2
2
4
同位角相等,两直线平行
内错角相等,两直线平行
c
b
4
3
2
1
a
复习回顾:
( )
(3)∵∠ +∠ =180°
∴ a∥b
2
3
同旁内角互补,两直线平行
4
3
2
1
a
c
b
复习回顾:
探索新知
2
7
2
5
6
3
1
8
4
2、将上图按照如下方式剪开,并分别把剪开得到的每对同位角、内错角重叠,你发现了什么?
?
做一做
?
探索新知:
2、将上图按照如下方式剪开,并分别把剪开得到的每对同位角重叠,你发现了什么?
?
做一做
?
7
2
5
6
两直线平行,同位角相等
3
1
8
4
探索新知:
两直线平行,同位角相等
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
符号语言:
b
1
2
a
c
同 位 角
2、将上图按照如下方式剪开,并分别把剪开得到的每对 重叠,你发现了什么?
?
做一做
?
8
4
7
2
5
6
3
1
两直线平行,内错角相等
内错角
探索新知:
两直线平行,内错角相等
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
符号语言:
b
1
2
a
c
3
内 错 角
你能根据”两直线平行,同位角相等”,说明“两直线平行,内错角相等”成立的理由吗?
a
b
c
1
2
3
解:
∵a∥b
∴∠1=∠2
如图所示
又∵ ∠1=∠3
(对顶角相等)
(已知)
(两直线平行,同位角相等)
∴∠2=∠3
(等量代换)
?
做一做
?
7
2
5
6
3、将图中的每对同旁内角剪成两部分,并把他们拼到一起去,你发现每对同旁内角之间有什么关系?
两直线平行,同旁内角互补.
7
3
1
8
4
2
探索新知:
两直线平行,同旁内角互补
∴∠2+∠3=180°
(两直线平行,同旁内角互补)
∵a∥b(已知)
符号语言:
a
3
2
b
同 旁 内 角
如果我们现在只知道“两直线平行,同位角相等”.你能说明“两直线平行,同旁内角互补”成立的理由吗?
∴ ∠2 + ∠3 = 180°
解:
如图所示
1
a
3
2
b
∵a∥b
(已知)
∴∠1=∠2
(两直线平行,同位角相等)
又∵ ∠1+∠3 = 180°
(平角定义)
(等量代换)
例题讲解
3
例1: 如图,已知直线a∥b,∠1 = 500,求∠2的度数.
a
b
c
1
2
∴∠ 2= 500 (等量代换).
解:∵ a∥b (已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
例题讲解:
A
B
C
D
2
1
例2: 如图:已知AB∥CD,求
∠A+∠B+∠ACB的度数.
解:∵AB∥CD(已知)
∴∠A=∠1(两直线平行,内错角相等)
∵ AB∥CD (已知)
∴∠B=∠2(两直线平行,同位角相等)
∴∠ A+∠B+∠ACB
= ∠1+ ∠2+ ∠ACB= 180°
例题讲解:
例3 :如图,AD∥BC, ∠A=∠C.
试说明AB∥DC
A
E
F
C
B
D
(同位角相等,两直线平行)
解:
∵AD∥BC(已知)
∴∠C=∠CDE
(两直线平行,内错角相等)
又∵ ∠A=∠C(已知)
∴ ∠A=∠CDE
(等量代换)
∴AB∥DC
例题讲解:
1.如图,若AB ∥ CD,则下列结论中
① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B
④ ∠B + ∠BCD= 180°正确的是 ( )
A ① ② B ① ③
C ① ④ D ③ ④
D
A
B
E
C
D
1
2
3
×
√
×
√
课堂反馈:
2.如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?
1420
B
C
A
D
?
解:
∵AB∥CD (已知),
∴∠B=∠C
(两直线平行,内错角相等).
又∵∠B=142° (已知),
∴∠B=∠C=142°
(等量代换).
课堂反馈:
3.如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数?
A
B
C
D
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800
(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).
②根据题目的已知条件,
无法求出∠A的度数.
课堂反馈:
4.如图,若AB ∥ ED,BC ∥ FE,则∠B + ∠E=_______
A
B
C
D
E
F
°
180
课堂反馈:
解:∵AB∥DE (已知)
∴∠B=∠BCE
(两直线平行,内错角相等)
∵BC∥FE(已知)
∴∠BCE+∠E=180?
(两直线平行,同旁内角互补)
∴∠B+∠E=180?(等量代换)
5.已知:如图,AB∥CD,∠1=∠2,
则GP与QH的位置关系是什么?并说明理由.
课堂反馈:
解:GP∥QH.
理由如下:
∵AB∥CD,
∴∠EGB=∠EHD.(两直线平行,同位角相等)
又∵∠1=∠2,∠EGP=∠EGB-∠1,∠EHQ=∠EHD-∠2,
∴∠EGP=∠EHQ,(等式的性质)
∴GP∥HQ.(同位角相等,两直线平行)
课堂小结
4
课堂小结:
通过本节课的学习,你有什么感悟?
(1)平行线的三条性质
(2)利用平行线的三条性质解计算题和简单
的解答题
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
