苏科版七年级数学下册第7章平面图形的认识(二)复习课件 (共25张PPT)
文档属性
| 名称 | 苏科版七年级数学下册第7章平面图形的认识(二)复习课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览


文档简介
初中数学七年级下册
(苏科版)
第7章 平面图形的认识(二)复习
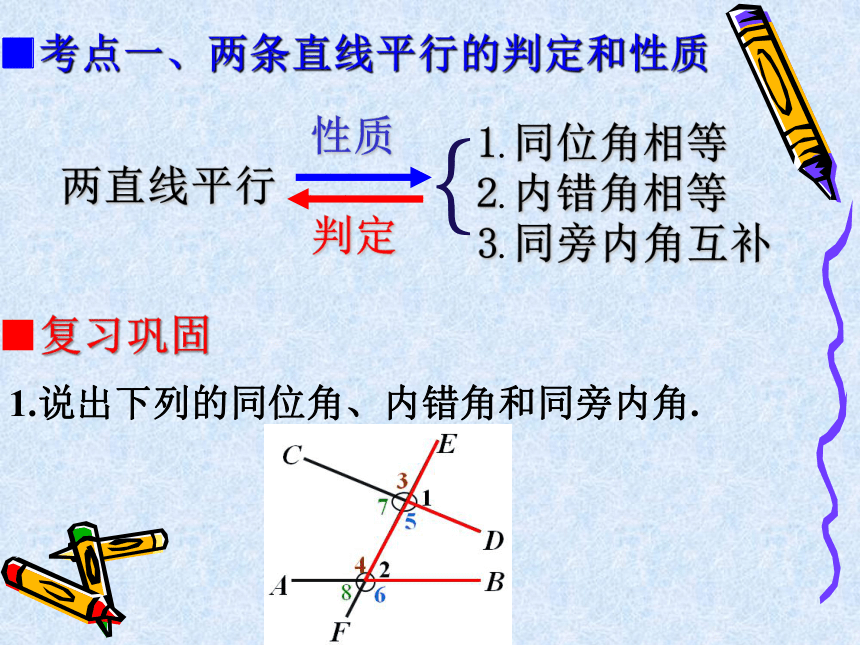
■考点一、两条直线平行的判定和性质
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.说出下列的同位角、内错角和同旁内角.
■复习巩固
2. 若两条直线被第三条直线所截,则( )
A.同位角相等 B.内错角相等
C.同旁内角互补 D.以上结论都不对
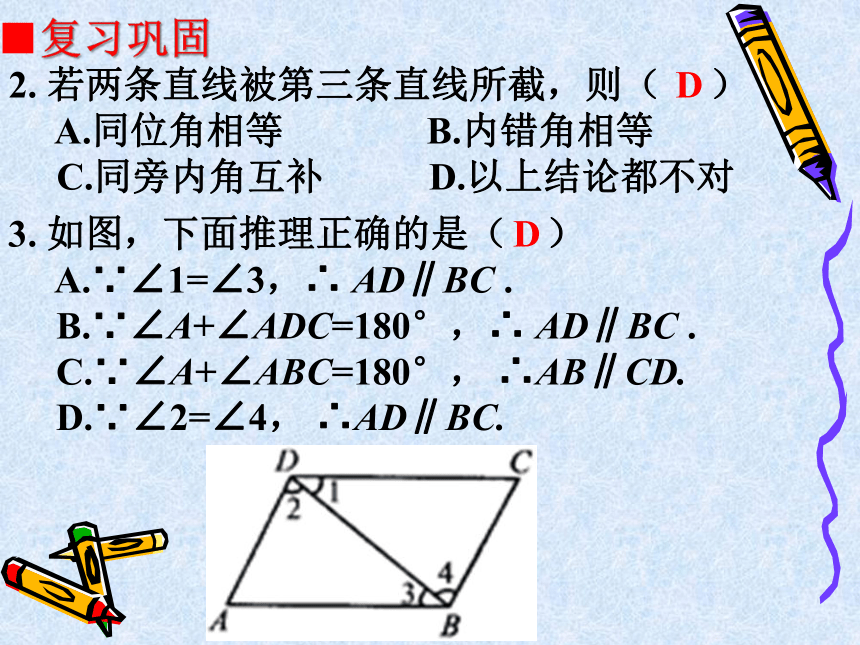
■复习巩固
3. 如图,下面推理正确的是( )
A.∵∠1=∠3,∴ AD∥BC .
B.∵∠A+∠ADC=180°,∴ AD∥BC .
C.∵∠A+∠ABC=180°, ∴AB∥CD.
D.∵∠2=∠4, ∴AD∥BC.
D
D
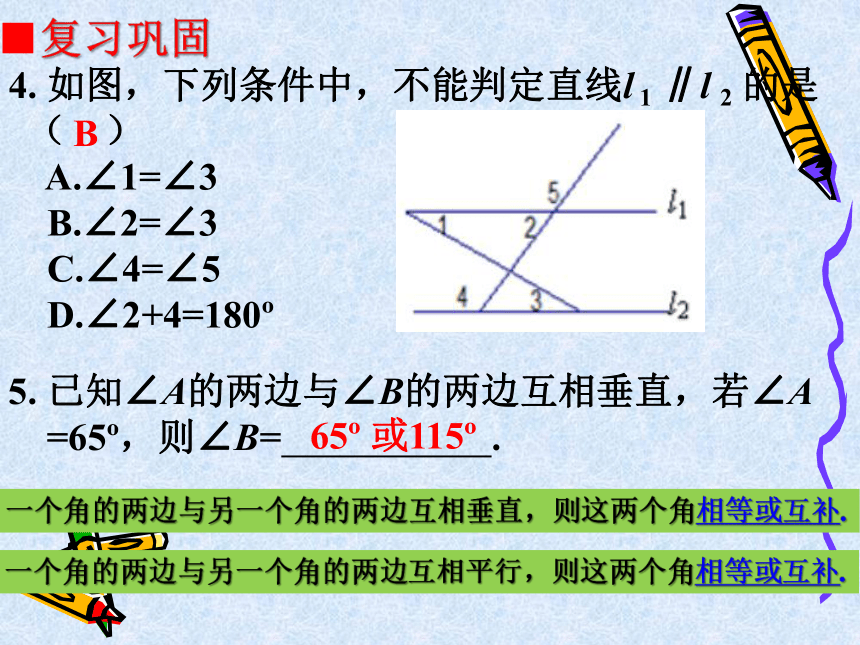
4. 如图,下列条件中,不能判定直线l 1 ∥l 2 的是
( )
A.∠1=∠3
B.∠2=∠3
C.∠4=∠5
D.∠2+4=180?
■复习巩固
5. 已知∠A的两边与∠B的两边互相垂直,若∠A
=65?,则∠B= .
B
65? 或115?
一个角的两边与另一个角的两边互相垂直,则这两个角相等或互补.
一个角的两边与另一个角的两边互相平行,则这两个角相等或互补.
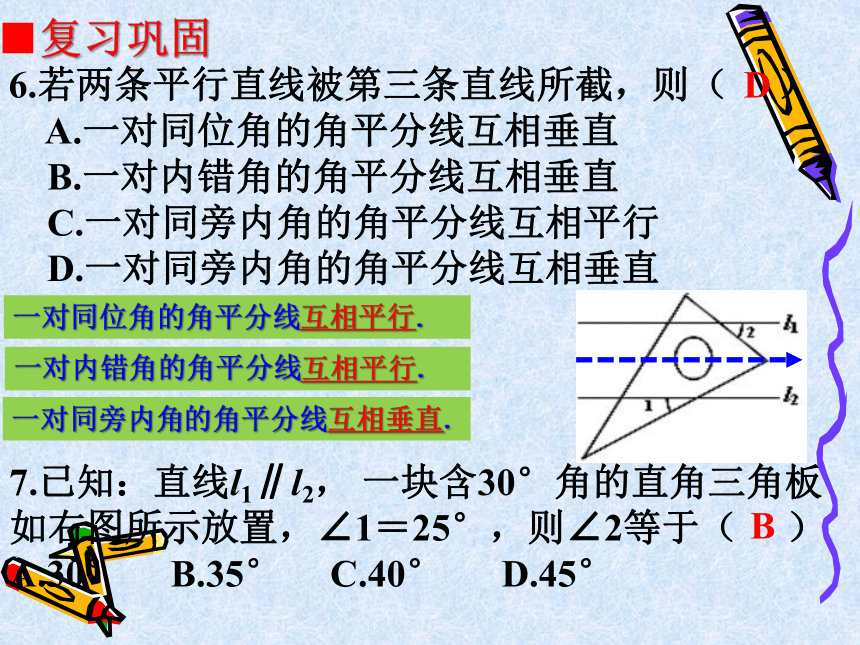
6.若两条平行直线被第三条直线所截,则( )
A.一对同位角的角平分线互相垂直
B.一对内错角的角平分线互相垂直
C.一对同旁内角的角平分线互相平行
D.一对同旁内角的角平分线互相垂直
■复习巩固
7.已知:直线l1∥l2, 一块含30°角的直角三角板如右图所示放置,∠1=25°,则∠2等于( )
A.30° B.35° C.40° D.45°
D
一对同位角的角平分线互相平行.
一对内错角的角平分线互相平行.
一对同旁内角的角平分线互相垂直.
B
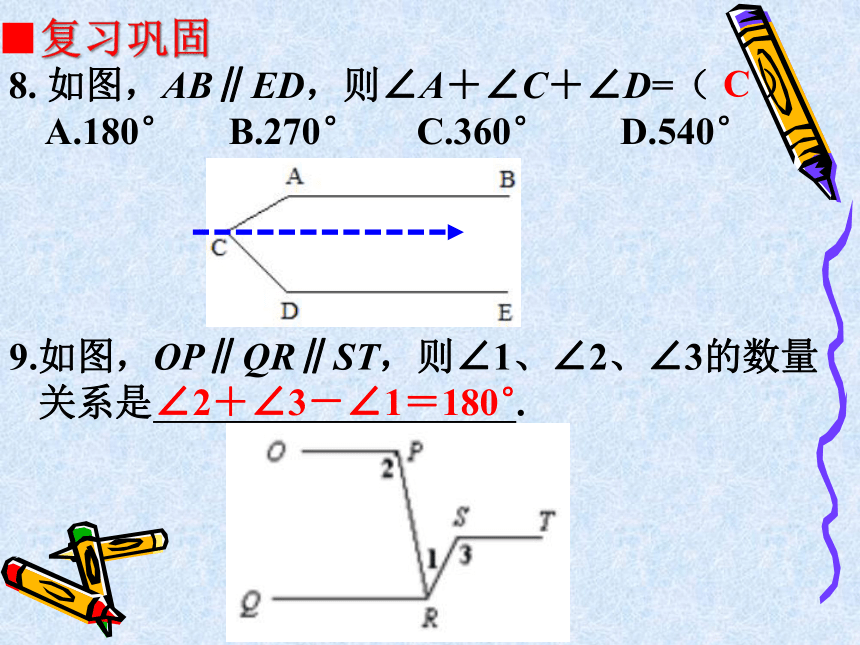
8. 如图,AB∥ED,则∠A+∠C+∠D=( )
A.180° B.270° C.360° D.540°
■复习巩固
9.如图,OP∥QR∥ST,则∠1、∠2、∠3的数量
关系是 .
C
∠2+∠3-∠1=180°
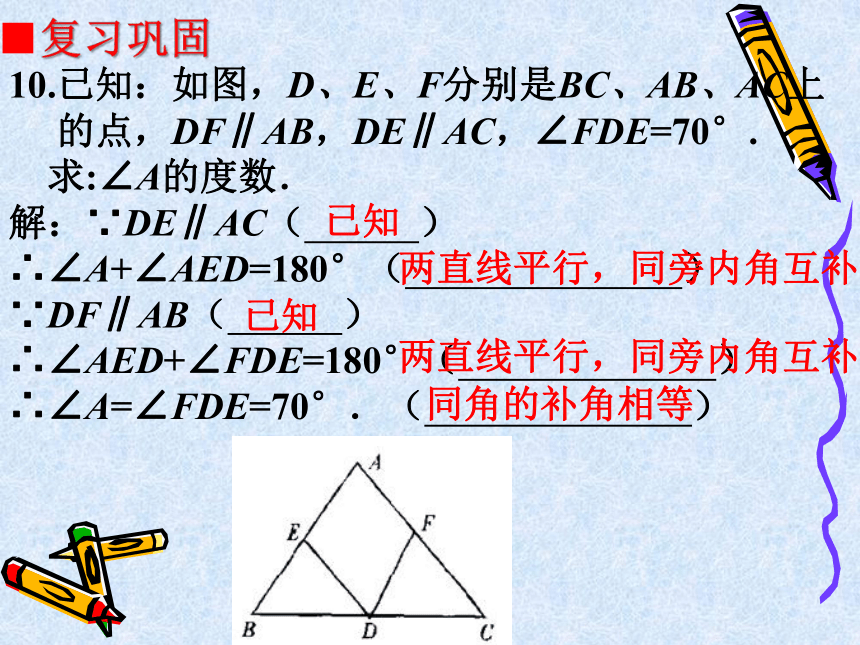
10.已知:如图,D、E、F分别是BC、AB、AC上
的点,DF∥AB,DE∥AC,∠FDE=70°.
求:∠A的度数.
解:∵DE∥AC( )
∴∠A+∠AED=180°( )
∵DF∥AB( )
∴∠AED+∠FDE=180°( )
∴∠A=∠FDE=70°.( )
■复习巩固
已知
两直线平行,同旁内角互补
已知
两直线平行,同旁内角互补
同角的补角相等
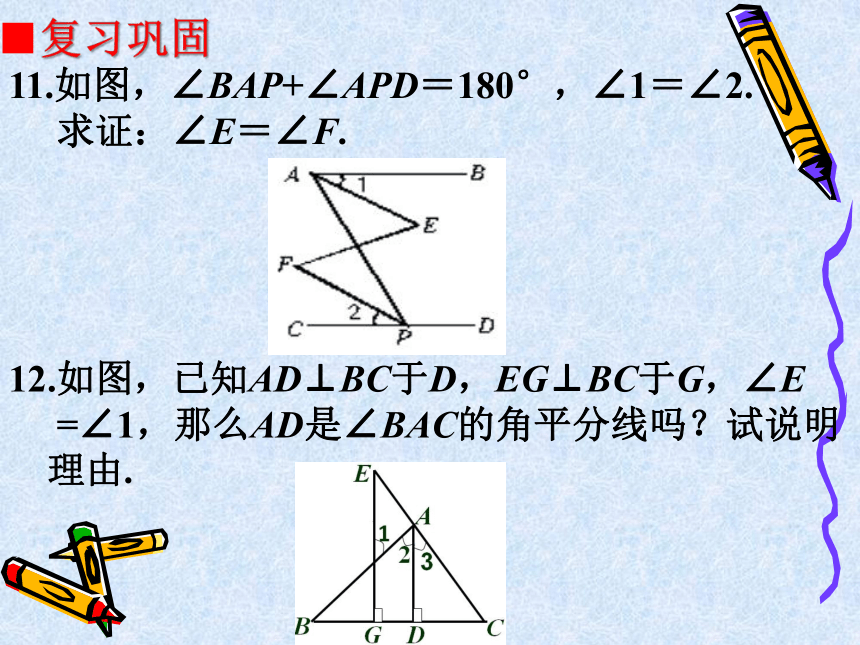
11.如图,∠BAP+∠APD=180°,∠1=∠2.
求证:∠E=∠F.
■复习巩固
12.如图,已知AD⊥BC于D,EG⊥BC于G,∠E
=∠1,那么AD是∠BAC的角平分线吗?试说明
理由.
■考点二、图形的平移
(1)平移不改变图形的形状和大小;
(2)对应线段平行(或在同一条直线上)且相等,对应角相等;
(3)对应点的连线平行(或在同一条直线上)且相等.
2.平移的性质
1.平移的两个要素:
(1)平移的方向(可以是水平方向、竖直方向、也可以是斜方向)
(2)平移的距离.
■复习巩固
13.如图,△ABC经过平移得到△A’B’C’,下列说
法错误的是( )
A. AA’=BB’ B. BB’//CC’
C. ∠B=∠A’ D. AC//A’ C’
C
14.将线段AB向右平移3cm得到对应线段CD,如果
AB=5 cm,则CD= cm, AC= cm.
5
3
15.不能通过其中一个四边形平移得到的是( )
D
■复习巩固
A1
B1
C1
2cm
2cm
2cm
16.画出把△ABC沿射线AD方向平移2cm后得到的
△A1B1C1.
D
■考点三、三角形相关知识
3.三角形的角平分线、中线、高
(1)三角形的角平分线、中线和高都是线段;
(2)三角形的3条角平分线相交于一点(锐角、直角、钝角三角
形的三条角平分线的交点都在其内部);
(3)三角形的3条中线相交于一点(锐角、直角、钝角三角形的
三条中线的交点都在其内部);
(4)三角形的3条高相交于一点(锐角、直角、钝角三角形的三
条高的交点分别在其内部、直角顶点、外部);
(5)三角形的一条中线把三角形的面积 分成相等的两部分(即
中线是三角形的面积等分线).
■考点三、三角形相关知识
1.三角形的分类
(1)按角的大小分类:锐角三角形、直角三角形和钝角三角形;
(2)按边长分类:不等边三角形、等腰三角形;
2.三角形的三边关系
(1)任意两边之和大于第三边;
(2)任意两边之差小于第三边.
■复习巩固
18.一个三角形的两边长分别为4和7,则第三边x的
取值范围是 .
17.有3、5、7、10的四根彩色线形木条,要摆出一
个三角形,有( )种摆法.
A.1 B.2 C.3 D.4
B
319. 一个等腰三角形的一边是5cm,另一边是7cm,
则这个三角形的周长是 .
17cm或19cm
20.下列各组图中,AD是△ABC 的高的是( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
■复习巩固
21.三角形三条高相交于一点,此点一定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的一条边上 D. 不能确定
22.如图,AD、BE是△ABC的中线,则下列结论
中,正确的个数有( )
(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE;(4)S△ABC=4S△BOC.
A. 1个 B. 2个 C. 3个 D. 4个
D
C
■考点四、三角形的内角和与外角和
1. n边形的内角和
(1)三角形的三个内角的和是180?;
(2)直角三角形的两个锐角互余;
(4)n边形的内角和等于 (n-2)·180°;
(3)三角形的一个外角等于与它不相邻的两个内角的和 ;
■考点四、三角形的内角和与外角和
2. n边形的外角和
n边形的外角和等于 360°;
■注意:
1. n边形的外角和是个定值(不随边数的变化而变化);
■复习巩固
23.一个多边形的内角和不可能是( )
A.360° B.910° C.1080° D.1800°
B
24.在△ABC中,∠A=2∠B=3∠C,则此三角形是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
C
25.已知在△ABC中,∠A:∠B:∠C=1:2:3,
最大内角的度数 .
90°
26.一个多边形的内角和为1440°,则它的边数为
.
十
27.一个多边形的每个内角都等于150°,则它的边
数为 .
十二
■复习巩固
28.一个多边形,它的内角和比外角和的4倍多
180°,求这个多边形的边数.
十一
29.在用计算器计算一个多边形的内角和时,小明
的结果为2005°,小芳立即判断他的结果是错
误的,小明仔细地复算了一遍,果然发现自己
把一个角的度数输入了两遍.根据以上事实,
多输的这个角度是 °,这个多边形的边数
是_________.
十三
25
■复习巩固
30.一个多边形截取一个角后,形成另一个多边形
的内角和是1620度,则原来多边形的边数是
A.10 B.11 C.12 D.以上都有可能
D
n边形减去一个角后,得到的多边形有可能是:
①(n-1)边形; ②n边形; ③(n+1)边形.
31.若n边形的内角和为12 60°,则从一个顶点出
发引的对角线条数是 .
6
过n边形的一个顶点可以画(n-3)条对角线.
32.(1)OB、OC分别是内角∠ABC、∠ACB的平分线,求∠O与∠A的数量关系.
■复习巩固
32.(2)OˊB、Oˊ C分别是外角∠DBC、∠ECB的平分线,求∠Oˊ 与∠A的数量关系.
■复习巩固
32.(3)Oˊˊ B、Oˊˊ C分别是内角∠ABC、外角∠ACD的平分线,求∠Oˊˊ 与∠A的数量关系.
■复习巩固
33.如图:△ABC纸片沿DE折叠,
使点A落在四边形BCDE的内部.
∠A与∠1+∠2之间存在怎样的
数量关系?请试着找出来,并说
明理由.
2
1
B
C
D
E
A
解: 2∠A= ∠1+∠2
在△ABC中,∠B+∠C=1800- ∠A
在△ADE中,∠ADE+∠AED= 1800- ∠A
在四边形BCDE中
∠B+∠C+∠1+∠2 +∠ADE+∠AED=3600,
所以 ∠1+∠2 +2(1800-∠A)=3600,
即 2∠A= ∠1+∠2.
■复习巩固
变式:如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的外部.∠A与∠1+∠2之间存在怎样的
数量关系?请试着找出来,并说
明理由.
解: 2∠A= ∠1-∠2
在四边形BCDE中
∠B+∠C+∠1+∠3 +∠4=3600,
所以 1800-∠A+∠1+(1800-∠2- ∠A)=3600,
即 2∠A= ∠1-∠2.
4
3
■复习巩固
(苏科版)
第7章 平面图形的认识(二)复习
■考点一、两条直线平行的判定和性质
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.说出下列的同位角、内错角和同旁内角.
■复习巩固
2. 若两条直线被第三条直线所截,则( )
A.同位角相等 B.内错角相等
C.同旁内角互补 D.以上结论都不对
■复习巩固
3. 如图,下面推理正确的是( )
A.∵∠1=∠3,∴ AD∥BC .
B.∵∠A+∠ADC=180°,∴ AD∥BC .
C.∵∠A+∠ABC=180°, ∴AB∥CD.
D.∵∠2=∠4, ∴AD∥BC.
D
D
4. 如图,下列条件中,不能判定直线l 1 ∥l 2 的是
( )
A.∠1=∠3
B.∠2=∠3
C.∠4=∠5
D.∠2+4=180?
■复习巩固
5. 已知∠A的两边与∠B的两边互相垂直,若∠A
=65?,则∠B= .
B
65? 或115?
一个角的两边与另一个角的两边互相垂直,则这两个角相等或互补.
一个角的两边与另一个角的两边互相平行,则这两个角相等或互补.
6.若两条平行直线被第三条直线所截,则( )
A.一对同位角的角平分线互相垂直
B.一对内错角的角平分线互相垂直
C.一对同旁内角的角平分线互相平行
D.一对同旁内角的角平分线互相垂直
■复习巩固
7.已知:直线l1∥l2, 一块含30°角的直角三角板如右图所示放置,∠1=25°,则∠2等于( )
A.30° B.35° C.40° D.45°
D
一对同位角的角平分线互相平行.
一对内错角的角平分线互相平行.
一对同旁内角的角平分线互相垂直.
B
8. 如图,AB∥ED,则∠A+∠C+∠D=( )
A.180° B.270° C.360° D.540°
■复习巩固
9.如图,OP∥QR∥ST,则∠1、∠2、∠3的数量
关系是 .
C
∠2+∠3-∠1=180°
10.已知:如图,D、E、F分别是BC、AB、AC上
的点,DF∥AB,DE∥AC,∠FDE=70°.
求:∠A的度数.
解:∵DE∥AC( )
∴∠A+∠AED=180°( )
∵DF∥AB( )
∴∠AED+∠FDE=180°( )
∴∠A=∠FDE=70°.( )
■复习巩固
已知
两直线平行,同旁内角互补
已知
两直线平行,同旁内角互补
同角的补角相等
11.如图,∠BAP+∠APD=180°,∠1=∠2.
求证:∠E=∠F.
■复习巩固
12.如图,已知AD⊥BC于D,EG⊥BC于G,∠E
=∠1,那么AD是∠BAC的角平分线吗?试说明
理由.
■考点二、图形的平移
(1)平移不改变图形的形状和大小;
(2)对应线段平行(或在同一条直线上)且相等,对应角相等;
(3)对应点的连线平行(或在同一条直线上)且相等.
2.平移的性质
1.平移的两个要素:
(1)平移的方向(可以是水平方向、竖直方向、也可以是斜方向)
(2)平移的距离.
■复习巩固
13.如图,△ABC经过平移得到△A’B’C’,下列说
法错误的是( )
A. AA’=BB’ B. BB’//CC’
C. ∠B=∠A’ D. AC//A’ C’
C
14.将线段AB向右平移3cm得到对应线段CD,如果
AB=5 cm,则CD= cm, AC= cm.
5
3
15.不能通过其中一个四边形平移得到的是( )
D
■复习巩固
A1
B1
C1
2cm
2cm
2cm
16.画出把△ABC沿射线AD方向平移2cm后得到的
△A1B1C1.
D
■考点三、三角形相关知识
3.三角形的角平分线、中线、高
(1)三角形的角平分线、中线和高都是线段;
(2)三角形的3条角平分线相交于一点(锐角、直角、钝角三角
形的三条角平分线的交点都在其内部);
(3)三角形的3条中线相交于一点(锐角、直角、钝角三角形的
三条中线的交点都在其内部);
(4)三角形的3条高相交于一点(锐角、直角、钝角三角形的三
条高的交点分别在其内部、直角顶点、外部);
(5)三角形的一条中线把三角形的面积 分成相等的两部分(即
中线是三角形的面积等分线).
■考点三、三角形相关知识
1.三角形的分类
(1)按角的大小分类:锐角三角形、直角三角形和钝角三角形;
(2)按边长分类:不等边三角形、等腰三角形;
2.三角形的三边关系
(1)任意两边之和大于第三边;
(2)任意两边之差小于第三边.
■复习巩固
18.一个三角形的两边长分别为4和7,则第三边x的
取值范围是 .
17.有3、5、7、10的四根彩色线形木条,要摆出一
个三角形,有( )种摆法.
A.1 B.2 C.3 D.4
B
3
则这个三角形的周长是 .
17cm或19cm
20.下列各组图中,AD是△ABC 的高的是( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
■复习巩固
21.三角形三条高相交于一点,此点一定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的一条边上 D. 不能确定
22.如图,AD、BE是△ABC的中线,则下列结论
中,正确的个数有( )
(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE;(4)S△ABC=4S△BOC.
A. 1个 B. 2个 C. 3个 D. 4个
D
C
■考点四、三角形的内角和与外角和
1. n边形的内角和
(1)三角形的三个内角的和是180?;
(2)直角三角形的两个锐角互余;
(4)n边形的内角和等于 (n-2)·180°;
(3)三角形的一个外角等于与它不相邻的两个内角的和 ;
■考点四、三角形的内角和与外角和
2. n边形的外角和
n边形的外角和等于 360°;
■注意:
1. n边形的外角和是个定值(不随边数的变化而变化);
■复习巩固
23.一个多边形的内角和不可能是( )
A.360° B.910° C.1080° D.1800°
B
24.在△ABC中,∠A=2∠B=3∠C,则此三角形是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
C
25.已知在△ABC中,∠A:∠B:∠C=1:2:3,
最大内角的度数 .
90°
26.一个多边形的内角和为1440°,则它的边数为
.
十
27.一个多边形的每个内角都等于150°,则它的边
数为 .
十二
■复习巩固
28.一个多边形,它的内角和比外角和的4倍多
180°,求这个多边形的边数.
十一
29.在用计算器计算一个多边形的内角和时,小明
的结果为2005°,小芳立即判断他的结果是错
误的,小明仔细地复算了一遍,果然发现自己
把一个角的度数输入了两遍.根据以上事实,
多输的这个角度是 °,这个多边形的边数
是_________.
十三
25
■复习巩固
30.一个多边形截取一个角后,形成另一个多边形
的内角和是1620度,则原来多边形的边数是
A.10 B.11 C.12 D.以上都有可能
D
n边形减去一个角后,得到的多边形有可能是:
①(n-1)边形; ②n边形; ③(n+1)边形.
31.若n边形的内角和为12 60°,则从一个顶点出
发引的对角线条数是 .
6
过n边形的一个顶点可以画(n-3)条对角线.
32.(1)OB、OC分别是内角∠ABC、∠ACB的平分线,求∠O与∠A的数量关系.
■复习巩固
32.(2)OˊB、Oˊ C分别是外角∠DBC、∠ECB的平分线,求∠Oˊ 与∠A的数量关系.
■复习巩固
32.(3)Oˊˊ B、Oˊˊ C分别是内角∠ABC、外角∠ACD的平分线,求∠Oˊˊ 与∠A的数量关系.
■复习巩固
33.如图:△ABC纸片沿DE折叠,
使点A落在四边形BCDE的内部.
∠A与∠1+∠2之间存在怎样的
数量关系?请试着找出来,并说
明理由.
2
1
B
C
D
E
A
解: 2∠A= ∠1+∠2
在△ABC中,∠B+∠C=1800- ∠A
在△ADE中,∠ADE+∠AED= 1800- ∠A
在四边形BCDE中
∠B+∠C+∠1+∠2 +∠ADE+∠AED=3600,
所以 ∠1+∠2 +2(1800-∠A)=3600,
即 2∠A= ∠1+∠2.
■复习巩固
变式:如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的外部.∠A与∠1+∠2之间存在怎样的
数量关系?请试着找出来,并说
明理由.
解: 2∠A= ∠1-∠2
在四边形BCDE中
∠B+∠C+∠1+∠3 +∠4=3600,
所以 1800-∠A+∠1+(1800-∠2- ∠A)=3600,
即 2∠A= ∠1-∠2.
4
3
■复习巩固
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
