苏科版七年级数学下册课件:7.1-7.2平行线的判定与性质复习课(共33张PPT)
文档属性
| 名称 | 苏科版七年级数学下册课件:7.1-7.2平行线的判定与性质复习课(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 14:46:49 | ||
图片预览



文档简介
平行线的判定
1.同位角相等,两直线平行。
2.内错角相等,两直线平行。
3.同旁内角互补,两直线平行。
平行线的性质
1.两直线平行,同位角相等。
2.两直线平行,内错角相等 。
3.两直线平行,同旁内角互补。
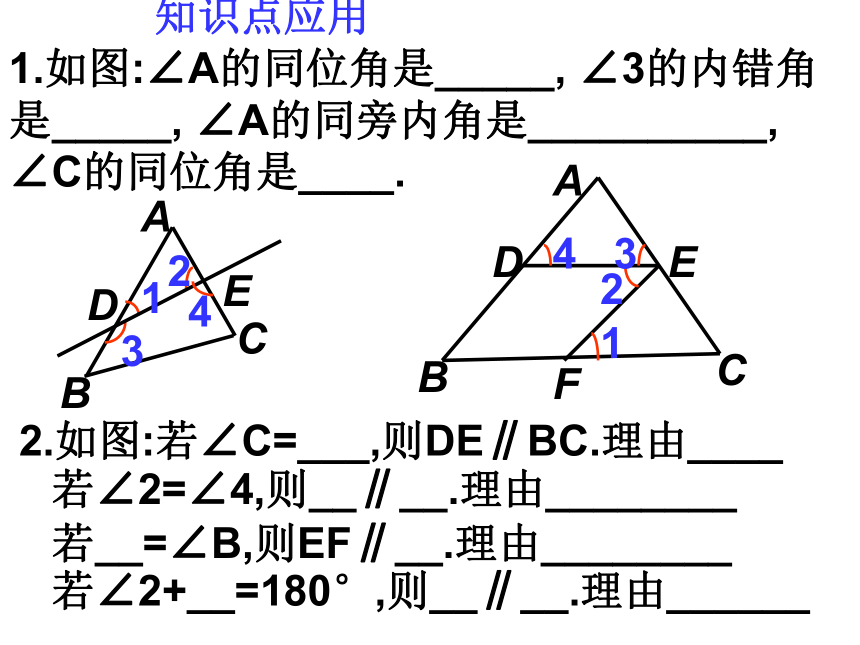
1.如图:∠A的同位角是_____, ∠3的内错角是_____, ∠A的同旁内角是__________, ∠C的同位角是____.
2.如图:若∠C=___,则DE∥BC.理由____
若∠2+__=180°,则__∥__.理由______
若__=∠B,则EF∥__.理由________
若∠2=∠4,则__∥__.理由________
A
B
C
D
E
1
2
3
4
知识点应用
A
B
C
D
E
F
1
2
3
4
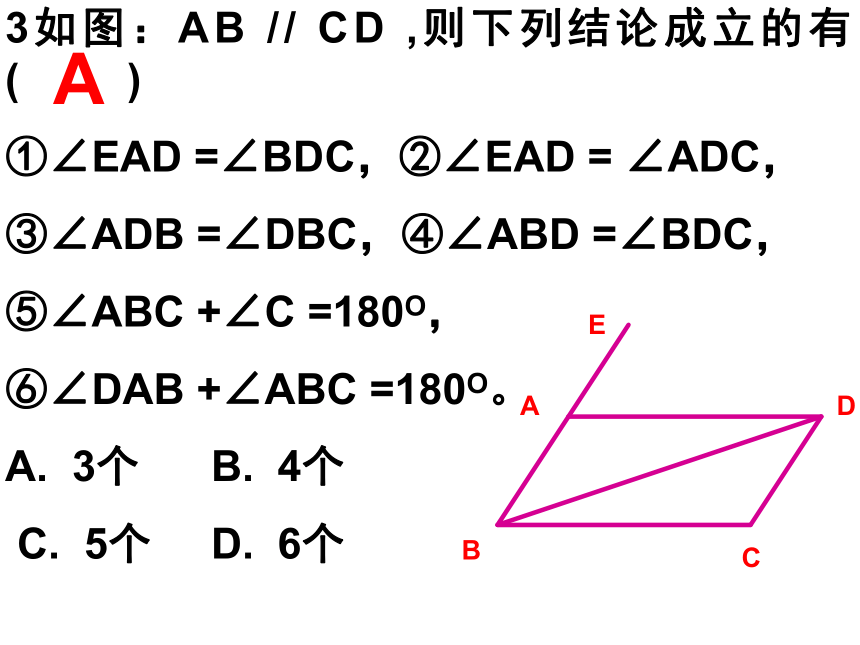
3如图:AB // CD ,则下列结论成立的有 ( )
①∠EAD =∠BDC,②∠EAD = ∠ADC,
③∠ADB =∠DBC,④∠ABD =∠BDC,
⑤∠ABC +∠C =180O,
⑥∠DAB +∠ABC =180O。
A. 3个 B. 4个
C. 5个 D. 6个
A
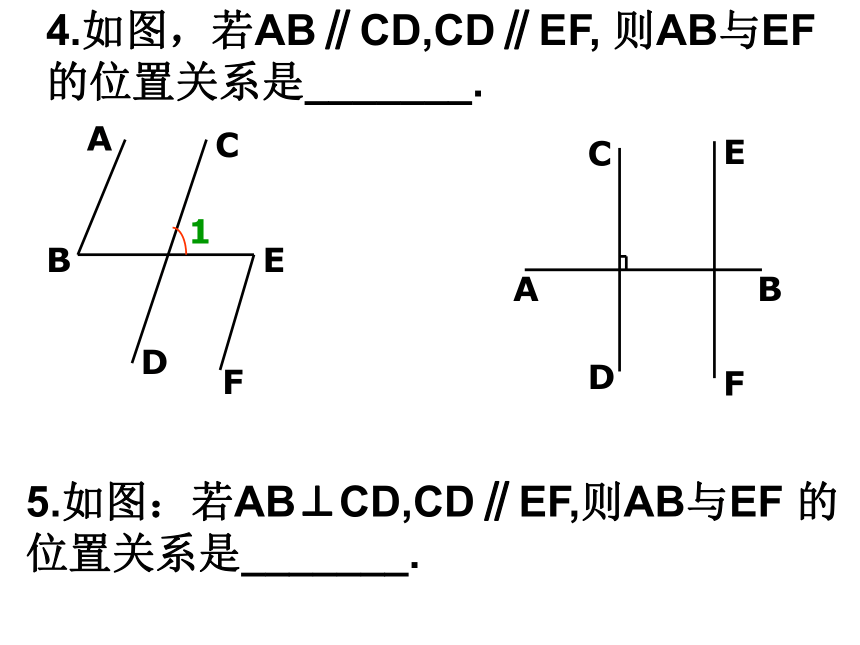
4.如图,若AB∥CD,CD∥EF, 则AB与EF的位置关系是_______.
5.如图:若AB⊥CD,CD∥EF,则AB与EF 的位置关系是_______.
A
B
C
D
E
F
1
A
B
C
D
E
F
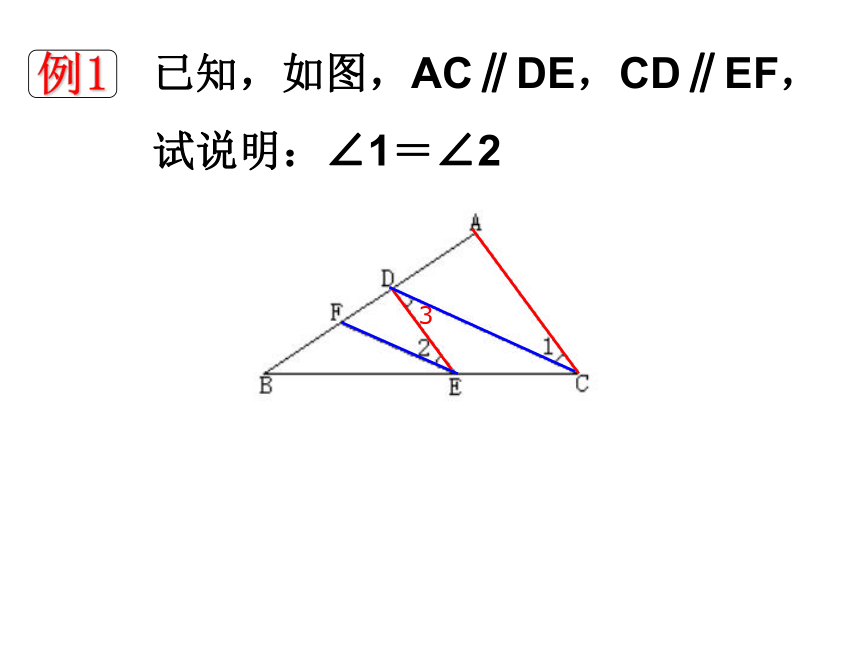
例1
已知,如图,AC∥DE,CD∥EF,
试说明:∠1=∠2
3
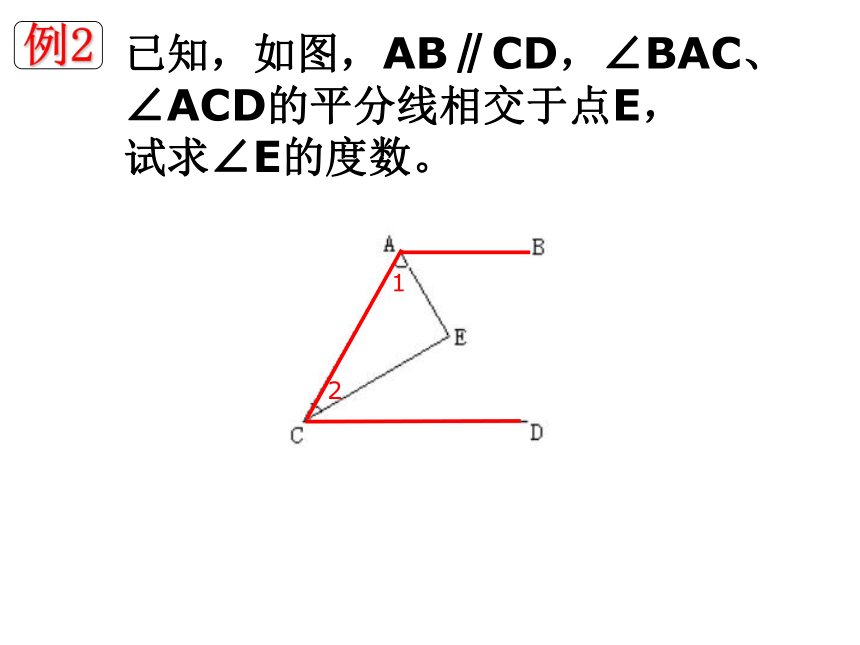
例2
已知,如图,AB∥CD,∠BAC、∠ACD的平分线相交于点E, 试求∠E的度数。
1
2
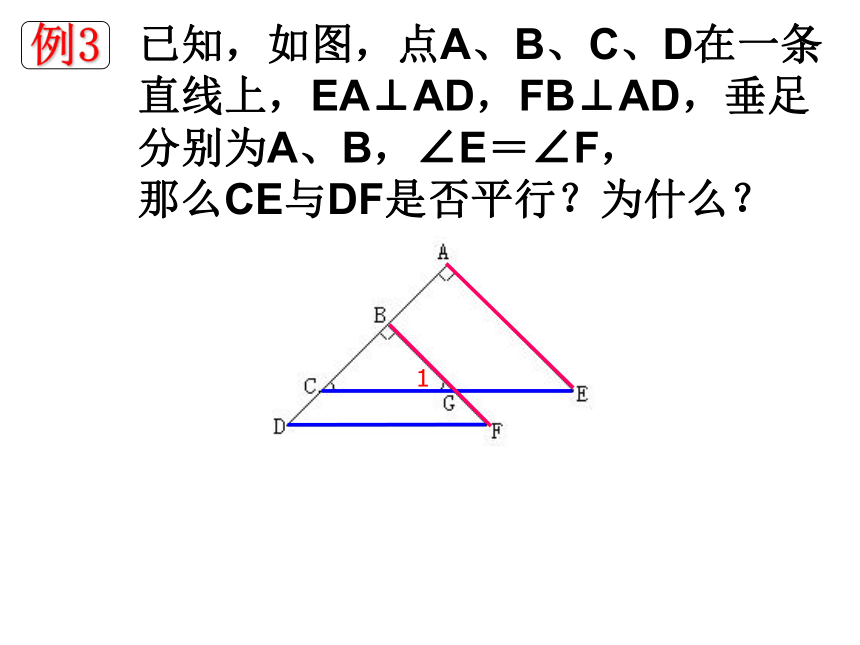
例3
已知,如图,点A、B、C、D在一条直线上,EA⊥AD,FB⊥AD,垂足分别为A、B,∠E=∠F, 那么CE与DF是否平行?为什么?
1
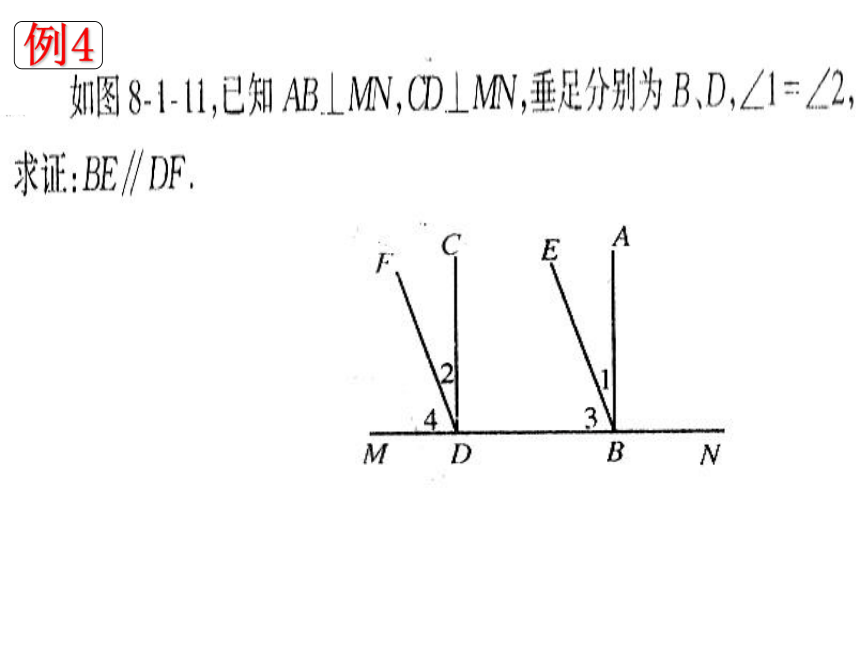
例4
例5
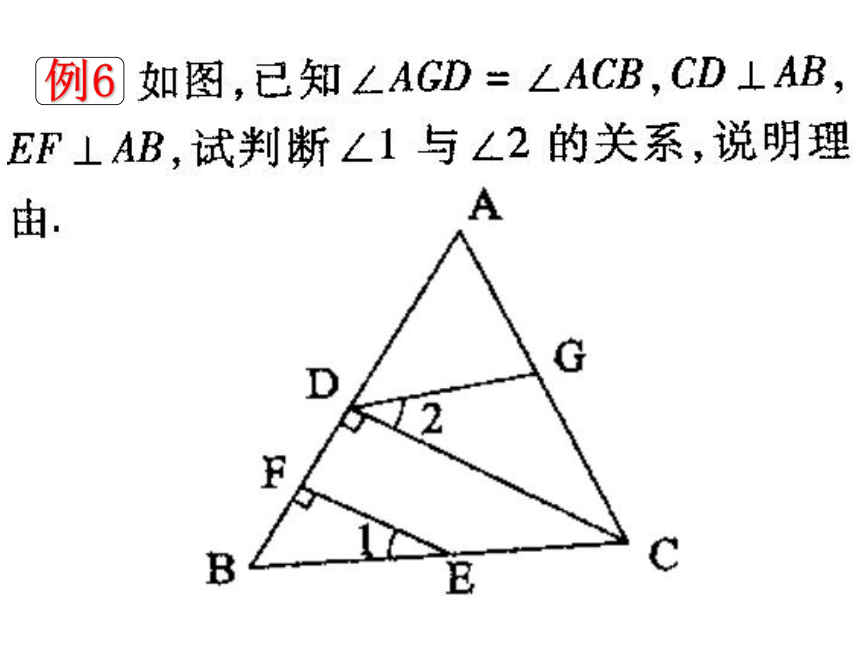
例6
例7
例8
练习:
1.在A、B两地之间修一条笔直的公路,从A地测得公路的走向为北偏东600,如果A、B两地同时开工,那么∠α是多少度时,才能使公路准确接通?
2.如图,一块钢板ABCD的两边AB、CD平行,要在AB上找一点E,使∠AEC=1500,应怎样确定点E的位置?为什么?
E
3.如图,∠1=∠2,∠3=1000,则∠4=___
4.如图,EG∥AB,FG∥DC,∠B=1000,∠C =1200,则 ∠EGF =_______
100
0
120
0
80
0
60
0
A
B
D
E
F
1
2
3
4
5.如图:已知AB∥CD, ∠1=∠4,
那么BE∥CF吗?为什么?
c
·
·
6.如图:已知AC平分∠BAD, ∠1=∠2, ∠B=70°. (1)试说明AB ∥ CD; (2)求 ∠BCD的度数
A
B
C
D
2
3
1
7.如图,将一张长方形纸片沿EF折叠后,点D、C分别落在D/、C/的位置,ED/的延长线与BC相交于点G,若∠EFG=500 , 求∠1、∠2的度数。
8.潜望镜中的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2、∠3=∠4,请解释为什么进入潜望镜的光线与离开潜望镜的光线是互相平行的。
5
6
9.如图,把一张长方形纸条沿EF折叠后, 点
B落在B1处,若∠ AEB1=700, 求∠MFD1的度数.
A
B
C
D
E
F
B1
D1
M
10.已知,AB∥CD,AC ∥BD, ∠1=72°.求∠2的度数.
A
B
C
D
2
3
1
11.已知:DE∥BC,∠1=∠2,∠D:∠DBC=2:1, 求∠3的度数.
D
E
B
C
2
1
3
12.如果两个角的两边分别平行,且其中一个角比另一个的3倍小200,则这两个角的度数分别是_______
13.如图,AB∥CD,∠DCB的平分线交DA的延长线于点E,交AB于点F,∠B与∠DAB互为补角,试探索∠E与∠AFE的大小关系,并说明理由。
D
E
A
C
B
F
北
南
14.从A地观测B地,B地位于A地的北偏东65°方向,则A地位于B地的什么方向?
A
B
北
南
西
东
65°
65°
西
东
解:A地位于B地的南偏西65°方向。
1.如图,已知AB∥CD ,∠B=230, ∠D=420,则∠E的度数为 ( )
A .230 B.420 C.650 D.190
A
B
C
D
E
F
链接中考:
2. 如图,已知AB∥DE ,∠B =600,∠CDE=1500,则∠BCE= .
A
B
C
D
600
1500
E
F
H
3.如图,已知AB∥DE ,∠ E=650,
则∠B+ ∠C的度数是( )
A .1350 B.1150 C.650 D.350
A
B
D
E
C
F
两类定理的比较
两条平行直线被第三条直线直线所截,
同位角相等, 两直线平行
两直线平行,同位角相等。
判定(数----形)
性质(形----数)
条件 结论
条件 结论
思考:
1、判定定理与性质定理的
条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定定理时是
已知 ,说明 ;
角的关系
两直线平行
使用性质定理时是
已知 ,说明 。
两直线平行
角的关系
在同一个平面内有2006条不同的直线a1,a2,a3, …,a2006,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么直线a1与a2006的位置关系是_______
找出能使下列结论成立的各种条件
(1)AB∥CD (2)∠1=∠2
A
B
F
E
D
C
1
2
1.同位角相等,两直线平行。
2.内错角相等,两直线平行。
3.同旁内角互补,两直线平行。
平行线的性质
1.两直线平行,同位角相等。
2.两直线平行,内错角相等 。
3.两直线平行,同旁内角互补。
1.如图:∠A的同位角是_____, ∠3的内错角是_____, ∠A的同旁内角是__________, ∠C的同位角是____.
2.如图:若∠C=___,则DE∥BC.理由____
若∠2+__=180°,则__∥__.理由______
若__=∠B,则EF∥__.理由________
若∠2=∠4,则__∥__.理由________
A
B
C
D
E
1
2
3
4
知识点应用
A
B
C
D
E
F
1
2
3
4
3如图:AB // CD ,则下列结论成立的有 ( )
①∠EAD =∠BDC,②∠EAD = ∠ADC,
③∠ADB =∠DBC,④∠ABD =∠BDC,
⑤∠ABC +∠C =180O,
⑥∠DAB +∠ABC =180O。
A. 3个 B. 4个
C. 5个 D. 6个
A
4.如图,若AB∥CD,CD∥EF, 则AB与EF的位置关系是_______.
5.如图:若AB⊥CD,CD∥EF,则AB与EF 的位置关系是_______.
A
B
C
D
E
F
1
A
B
C
D
E
F
例1
已知,如图,AC∥DE,CD∥EF,
试说明:∠1=∠2
3
例2
已知,如图,AB∥CD,∠BAC、∠ACD的平分线相交于点E, 试求∠E的度数。
1
2
例3
已知,如图,点A、B、C、D在一条直线上,EA⊥AD,FB⊥AD,垂足分别为A、B,∠E=∠F, 那么CE与DF是否平行?为什么?
1
例4
例5
例6
例7
例8
练习:
1.在A、B两地之间修一条笔直的公路,从A地测得公路的走向为北偏东600,如果A、B两地同时开工,那么∠α是多少度时,才能使公路准确接通?
2.如图,一块钢板ABCD的两边AB、CD平行,要在AB上找一点E,使∠AEC=1500,应怎样确定点E的位置?为什么?
E
3.如图,∠1=∠2,∠3=1000,则∠4=___
4.如图,EG∥AB,FG∥DC,∠B=1000,∠C =1200,则 ∠EGF =_______
100
0
120
0
80
0
60
0
A
B
D
E
F
1
2
3
4
5.如图:已知AB∥CD, ∠1=∠4,
那么BE∥CF吗?为什么?
c
·
·
6.如图:已知AC平分∠BAD, ∠1=∠2, ∠B=70°. (1)试说明AB ∥ CD; (2)求 ∠BCD的度数
A
B
C
D
2
3
1
7.如图,将一张长方形纸片沿EF折叠后,点D、C分别落在D/、C/的位置,ED/的延长线与BC相交于点G,若∠EFG=500 , 求∠1、∠2的度数。
8.潜望镜中的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2、∠3=∠4,请解释为什么进入潜望镜的光线与离开潜望镜的光线是互相平行的。
5
6
9.如图,把一张长方形纸条沿EF折叠后, 点
B落在B1处,若∠ AEB1=700, 求∠MFD1的度数.
A
B
C
D
E
F
B1
D1
M
10.已知,AB∥CD,AC ∥BD, ∠1=72°.求∠2的度数.
A
B
C
D
2
3
1
11.已知:DE∥BC,∠1=∠2,∠D:∠DBC=2:1, 求∠3的度数.
D
E
B
C
2
1
3
12.如果两个角的两边分别平行,且其中一个角比另一个的3倍小200,则这两个角的度数分别是_______
13.如图,AB∥CD,∠DCB的平分线交DA的延长线于点E,交AB于点F,∠B与∠DAB互为补角,试探索∠E与∠AFE的大小关系,并说明理由。
D
E
A
C
B
F
北
南
14.从A地观测B地,B地位于A地的北偏东65°方向,则A地位于B地的什么方向?
A
B
北
南
西
东
65°
65°
西
东
解:A地位于B地的南偏西65°方向。
1.如图,已知AB∥CD ,∠B=230, ∠D=420,则∠E的度数为 ( )
A .230 B.420 C.650 D.190
A
B
C
D
E
F
链接中考:
2. 如图,已知AB∥DE ,∠B =600,∠CDE=1500,则∠BCE= .
A
B
C
D
600
1500
E
F
H
3.如图,已知AB∥DE ,∠ E=650,
则∠B+ ∠C的度数是( )
A .1350 B.1150 C.650 D.350
A
B
D
E
C
F
两类定理的比较
两条平行直线被第三条直线直线所截,
同位角相等, 两直线平行
两直线平行,同位角相等。
判定(数----形)
性质(形----数)
条件 结论
条件 结论
思考:
1、判定定理与性质定理的
条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定定理时是
已知 ,说明 ;
角的关系
两直线平行
使用性质定理时是
已知 ,说明 。
两直线平行
角的关系
在同一个平面内有2006条不同的直线a1,a2,a3, …,a2006,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么直线a1与a2006的位置关系是_______
找出能使下列结论成立的各种条件
(1)AB∥CD (2)∠1=∠2
A
B
F
E
D
C
1
2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
