苏科版七年级下册数学:8.1 同底数幂的乘法 (共20张PPT)
文档属性
| 名称 | 苏科版七年级下册数学:8.1 同底数幂的乘法 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 406.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:12:24 | ||
图片预览








文档简介
8.1 同底数幂的乘法
欢迎各位领导、专家莅位指导
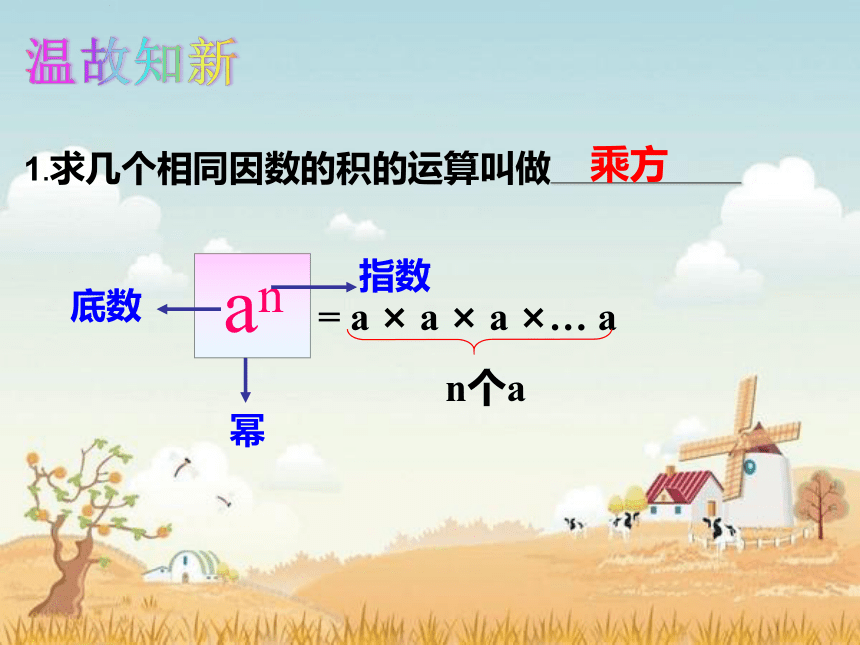
an
底数
幂
指数
= a × a × a ×… a
n个a
温故知新
1.求几个相同因数的积的运算叫做_______________
乘方
回顾热身
(1)25 表示
(2)
(3)a的底数是 ,指数是
(4)(a+b)3 的底数是 ,指数是
(5)(-2)4 的底数是 ,指数是
(6)-2 4 的底数是 ,指数是
10×10 ×10 ×10 可以写成
_______________
_______________
_______________
_______________
_______________
________
_______________
_______________
_______
_______________
2×2 × 2× 2× 2
104
a
1
(a+b)
3
-2
4
2
4
速度×时间=距离
光在真空中的速度大约是3×108 米/秒,太阳光照射到地球表面所需时间约为5×102秒,地球与太阳之间的距离约是多少?
探索新知
如何计算 108×102 ?
(3×108 ) ×(5×102)
=(3×5)×(108×102)
(1) 108×102 =( )×( )
=( )=( )
8个10
10个10
(2)a2 ×a3=( ) ×( )
=( )=( )
10 ×10 ×10 … ×10
10 ×10
10 × 10 × 10 × … 10
1010
a × a
a × a × a
a × a × a × a × a
a5
(3)am ×an=( ) ×( )
【m,n都是正整数】=( )=( )
a × a × … ×a
a × a × … ×a
m个a
n个a
a × a × … ×a
(m+n)个a
a m+n
思考 观察上面等式左右两边,底数、指数有怎样
的关系?
同底数幂的乘法法则
获取新知
同底数幂相乘,底数 ,指数
_______________
_______________
不变
相加
am · an = am+n (当m、n都是正整数)
条件: (1)乘法 (2)同底数幂
结果: (1)底数不变 (2)指数相加
例如:1014×103=( )=( )
1017×102 =( )
1014+3
1017
1019
1014×103×102=( )
1019
拓展延伸
想一想 :当三个或三个以上同底数幂
相乘时,是否也有这种性质呢?
am· an· a p = (m,n,p都是正整数)
am+n+p
直接应用公式
口答:(1)78 × 73=
(2)105 × 105=
(3)3 × 33=
(4)(-2)2×(-2)=
(5)( )3×( )4=
(6)am · a3=
711
1010
34
(-2)3
= -8
( )7
am+3
1
例1:计算
(1)-a2·a6
(2)x·x2·x3
(3)(-x)·(-x)3
(4)c3m·c2m-1(m为正整数)
想一想
(x+y)3 · (x+y)4
解:原式=(x+y)3+4
=(x+y)7
公式中的a可代表单项式,也可代表多项式
课堂小结
1
2
3
1.同底数幂相乘,底数不变,指数相加。
2.解题时,是什么运算就应用什么法则。
如:
3.-a2 的底数是a,而不是-a。
4.公式中的底数a可以是单项式,也可以是多项式。如果是多项式,要把它看成一个整体进行计算。
a3 · a3 =
a3 +a3 =
a6
2a3
判断对错
下面的计算对不对?如果不对,怎么样改正?
(1)b5 · b5 = 2b5 ( )
(2)b5 + b5 = b10 ( )
(3)x5 ? x2= x10 ( )
(4)y5 + 2y5 = 3y10 ( )
(5)c ? c3 = c3 ( )
(6)m + m3 = m4 ( )
x
x
x
x
x
b5 · b5 = b10
b5 + b5 =2b5
x5 ? x2 = x7
y5 + 2y5 = 3y5
c ? c3 = c4
x
填空:
(1) 8 = 2x , 则 x = ______________;
(2)8 × 4 = 2x ,则 x = ____________;
(3)3 × 27 × 9 = 3x ,则 x = ________;
↓
23
3
↓
↓
23 × 22 =
5
↓
↓
↓
3 × 33 × 32 =
6
25
36
灵活运用
? ? ?
(1) x6 ? ( )=x9
(2) a ? ( )= a6
(3) x ? x3 ?( )=x7
(4) xm ? ( )= x3m
x3
a5
x3
x2m
逆向转换
公式逆用:
am+n = am ? an (m,n是正整数)
已知:
am = 2 , an = 3.
求 am+n .
解:
am+n = am ? an
= 2 × 3 = 6
逆向转换
1. 已知: a5 = 7; a3 = 16. 则 a8 =( )
112
2.已知2m = a , 2n = b ,(m,n都是正整数),则2m+n = ( )
ab
a8 = a5+3 = a5 ? a3
= 7×16 = 112
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
我的收获
知识
方法
特殊 → 一般 → 特殊
例子 公式 应用
不变,
相加.
→
→
总结反思
放松一下
夜空无数的明星中,除了少数行星外(如金星,木星,地球等),都是自己会发光的恒星,恒星发光的强度各不相同。
“心宿(xiu)二”是夏季夜空中最亮的一颗恒星,“心宿二”距离我们大约400光年,它的表面温度大约是3000℃,只是太阳表面温度的一半,它的直径为太阳的600倍,但它的质量却只有太阳的25倍,平均密度不到太阳的860万分之一。
作业:
1.《同步练习》对应的内容
2. 复习本节课内容
谢谢指导!
欢迎各位领导、专家莅位指导
an
底数
幂
指数
= a × a × a ×… a
n个a
温故知新
1.求几个相同因数的积的运算叫做_______________
乘方
回顾热身
(1)25 表示
(2)
(3)a的底数是 ,指数是
(4)(a+b)3 的底数是 ,指数是
(5)(-2)4 的底数是 ,指数是
(6)-2 4 的底数是 ,指数是
10×10 ×10 ×10 可以写成
_______________
_______________
_______________
_______________
_______________
________
_______________
_______________
_______
_______________
2×2 × 2× 2× 2
104
a
1
(a+b)
3
-2
4
2
4
速度×时间=距离
光在真空中的速度大约是3×108 米/秒,太阳光照射到地球表面所需时间约为5×102秒,地球与太阳之间的距离约是多少?
探索新知
如何计算 108×102 ?
(3×108 ) ×(5×102)
=(3×5)×(108×102)
(1) 108×102 =( )×( )
=( )=( )
8个10
10个10
(2)a2 ×a3=( ) ×( )
=( )=( )
10 ×10 ×10 … ×10
10 ×10
10 × 10 × 10 × … 10
1010
a × a
a × a × a
a × a × a × a × a
a5
(3)am ×an=( ) ×( )
【m,n都是正整数】=( )=( )
a × a × … ×a
a × a × … ×a
m个a
n个a
a × a × … ×a
(m+n)个a
a m+n
思考 观察上面等式左右两边,底数、指数有怎样
的关系?
同底数幂的乘法法则
获取新知
同底数幂相乘,底数 ,指数
_______________
_______________
不变
相加
am · an = am+n (当m、n都是正整数)
条件: (1)乘法 (2)同底数幂
结果: (1)底数不变 (2)指数相加
例如:1014×103=( )=( )
1017×102 =( )
1014+3
1017
1019
1014×103×102=( )
1019
拓展延伸
想一想 :当三个或三个以上同底数幂
相乘时,是否也有这种性质呢?
am· an· a p = (m,n,p都是正整数)
am+n+p
直接应用公式
口答:(1)78 × 73=
(2)105 × 105=
(3)3 × 33=
(4)(-2)2×(-2)=
(5)( )3×( )4=
(6)am · a3=
711
1010
34
(-2)3
= -8
( )7
am+3
1
例1:计算
(1)-a2·a6
(2)x·x2·x3
(3)(-x)·(-x)3
(4)c3m·c2m-1(m为正整数)
想一想
(x+y)3 · (x+y)4
解:原式=(x+y)3+4
=(x+y)7
公式中的a可代表单项式,也可代表多项式
课堂小结
1
2
3
1.同底数幂相乘,底数不变,指数相加。
2.解题时,是什么运算就应用什么法则。
如:
3.-a2 的底数是a,而不是-a。
4.公式中的底数a可以是单项式,也可以是多项式。如果是多项式,要把它看成一个整体进行计算。
a3 · a3 =
a3 +a3 =
a6
2a3
判断对错
下面的计算对不对?如果不对,怎么样改正?
(1)b5 · b5 = 2b5 ( )
(2)b5 + b5 = b10 ( )
(3)x5 ? x2= x10 ( )
(4)y5 + 2y5 = 3y10 ( )
(5)c ? c3 = c3 ( )
(6)m + m3 = m4 ( )
x
x
x
x
x
b5 · b5 = b10
b5 + b5 =2b5
x5 ? x2 = x7
y5 + 2y5 = 3y5
c ? c3 = c4
x
填空:
(1) 8 = 2x , 则 x = ______________;
(2)8 × 4 = 2x ,则 x = ____________;
(3)3 × 27 × 9 = 3x ,则 x = ________;
↓
23
3
↓
↓
23 × 22 =
5
↓
↓
↓
3 × 33 × 32 =
6
25
36
灵活运用
? ? ?
(1) x6 ? ( )=x9
(2) a ? ( )= a6
(3) x ? x3 ?( )=x7
(4) xm ? ( )= x3m
x3
a5
x3
x2m
逆向转换
公式逆用:
am+n = am ? an (m,n是正整数)
已知:
am = 2 , an = 3.
求 am+n .
解:
am+n = am ? an
= 2 × 3 = 6
逆向转换
1. 已知: a5 = 7; a3 = 16. 则 a8 =( )
112
2.已知2m = a , 2n = b ,(m,n都是正整数),则2m+n = ( )
ab
a8 = a5+3 = a5 ? a3
= 7×16 = 112
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
我的收获
知识
方法
特殊 → 一般 → 特殊
例子 公式 应用
不变,
相加.
→
→
总结反思
放松一下
夜空无数的明星中,除了少数行星外(如金星,木星,地球等),都是自己会发光的恒星,恒星发光的强度各不相同。
“心宿(xiu)二”是夏季夜空中最亮的一颗恒星,“心宿二”距离我们大约400光年,它的表面温度大约是3000℃,只是太阳表面温度的一半,它的直径为太阳的600倍,但它的质量却只有太阳的25倍,平均密度不到太阳的860万分之一。
作业:
1.《同步练习》对应的内容
2. 复习本节课内容
谢谢指导!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
