苏科版七年级下册数学课件:9.5 因式分解的意义,提公因式法 (共17张PPT)
文档属性
| 名称 | 苏科版七年级下册数学课件:9.5 因式分解的意义,提公因式法 (共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:20:07 | ||
图片预览






文档简介
9.5 多项式的因式分解(1)
一、复习旧知 温故知新
1. 计算下列各式:
3x(x-1)= _____
m(a+b+c) = _____
(m+4)(m-4)= ____
(x-3)2= ________
(x+2)(x+1)= ____
根据左面的算式填空:
(1) 3x2-3x=_______
(2)ma+mb+mc=_____
(3) m2-16=___________
(4) x2-6x+9=________
(5)x2+3x+2=________
二、自主探究(围绕学习目标自学课本81页、82页)
观察上式,思考什么是因式分解
把一个多项式写成几个整式的积的形式,叫做多项式的因式分解。
也叫做把这个多项式分解因式
下列各式由左到右的变形那些是因式分解
ab+ac+d=a(b+c)+d
a2-1=(a+1)(a-1)
(3) (a+1)(a-1) = a2-1
(4) x2+1=x(x+ )
计算:375×2.8+375×4.9+375×2.3
三、合作探究一
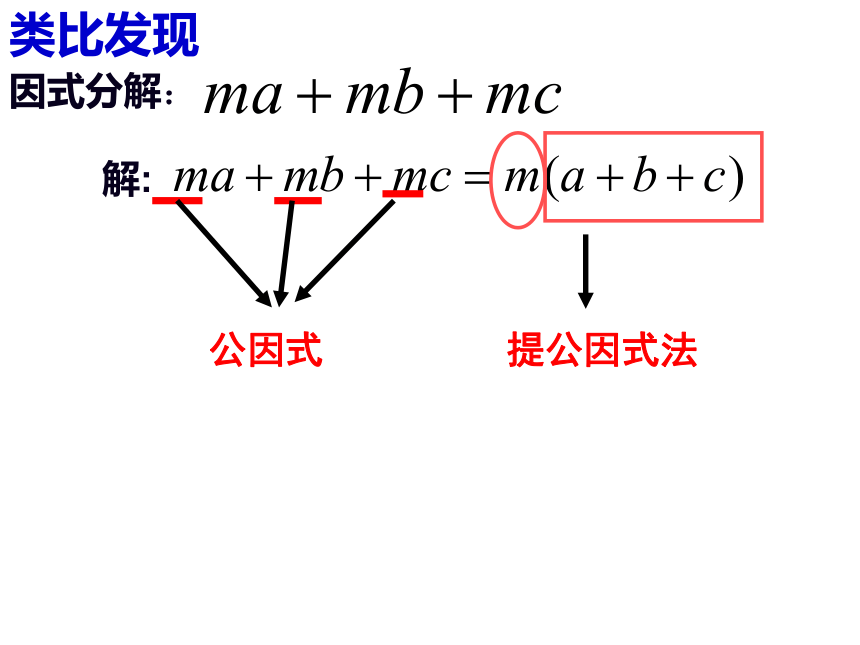
因式分解:
类比发现
解:
公因式
提公因式法
试一试:下列多项式的各项是否有公因式?如果有,试找出公因式.
(1) 6a+8b
(2) ab-ac
(3) m3n2+m2n5
(4) 2x2-6x3y
(5) a(x+y)-c(x+y)2
a
2
交流思考:如何找多项式的公因式?
x+y
m2n2
2x2
公因式既可以是单项式也可以是多项式
公因式:
(1)看系数:取各项系数的最大公约数
(2)看字母:取各项相同字母的最低次数
(3)看多项式:取各项相同多项式的最低次数
找出下列多项式各项的公因式
(1)9abc-6a2b2+12abc2
(2)3an+1-6an+9an-1
(3)14(n+m)2-35(n+m)3
三看
填空并说说你的方法
(1) a2b+ab2 = ab( )
(3)3(x+y)2+(x+y)3=(x+y)2( )
(2)9abc-6a2b2 =3ab( )
把下列多项式写成乘积的形式
a+b
3+x+y
ma+mb+mc m(a+b+c)
因式分解
整式乘法
(单项式乘多项式)
3c-2ab
合作探究二
(1) 8a3b2 + 12ab3c;
把下列各式分解因式:
(2) 2a(b+c) - 3(b+c).
例2
(3)8a3b2 –12ab 3 c + ab
(4) – 24x3 –12x2 +28x
四、检测展示
把下列各式分解因式:
(1)15a3b2+5a2b
(2)6x3y-18xy2-3xy
(3)-x2y+4xy-5y2
(4)p(a2 + b2 )- q(a2 + b2 )
+
+
(1)
992+99.
(2)
5计算:
6.已知: 2x+y=4,xy=3,
求代数式2x2y+xy2的值
这节课你有哪些收获?
六、课堂小结
七 拓展作业
1.(必做题)课本P87习题第1、2题;
2. (选做题)思考:
(1)20042+2004能被2005整除吗?
(2)如果n是自然数,那么n2+n是奇数还是偶数?
一、复习旧知 温故知新
1. 计算下列各式:
3x(x-1)= _____
m(a+b+c) = _____
(m+4)(m-4)= ____
(x-3)2= ________
(x+2)(x+1)= ____
根据左面的算式填空:
(1) 3x2-3x=_______
(2)ma+mb+mc=_____
(3) m2-16=___________
(4) x2-6x+9=________
(5)x2+3x+2=________
二、自主探究(围绕学习目标自学课本81页、82页)
观察上式,思考什么是因式分解
把一个多项式写成几个整式的积的形式,叫做多项式的因式分解。
也叫做把这个多项式分解因式
下列各式由左到右的变形那些是因式分解
ab+ac+d=a(b+c)+d
a2-1=(a+1)(a-1)
(3) (a+1)(a-1) = a2-1
(4) x2+1=x(x+ )
计算:375×2.8+375×4.9+375×2.3
三、合作探究一
因式分解:
类比发现
解:
公因式
提公因式法
试一试:下列多项式的各项是否有公因式?如果有,试找出公因式.
(1) 6a+8b
(2) ab-ac
(3) m3n2+m2n5
(4) 2x2-6x3y
(5) a(x+y)-c(x+y)2
a
2
交流思考:如何找多项式的公因式?
x+y
m2n2
2x2
公因式既可以是单项式也可以是多项式
公因式:
(1)看系数:取各项系数的最大公约数
(2)看字母:取各项相同字母的最低次数
(3)看多项式:取各项相同多项式的最低次数
找出下列多项式各项的公因式
(1)9abc-6a2b2+12abc2
(2)3an+1-6an+9an-1
(3)14(n+m)2-35(n+m)3
三看
填空并说说你的方法
(1) a2b+ab2 = ab( )
(3)3(x+y)2+(x+y)3=(x+y)2( )
(2)9abc-6a2b2 =3ab( )
把下列多项式写成乘积的形式
a+b
3+x+y
ma+mb+mc m(a+b+c)
因式分解
整式乘法
(单项式乘多项式)
3c-2ab
合作探究二
(1) 8a3b2 + 12ab3c;
把下列各式分解因式:
(2) 2a(b+c) - 3(b+c).
例2
(3)8a3b2 –12ab 3 c + ab
(4) – 24x3 –12x2 +28x
四、检测展示
把下列各式分解因式:
(1)15a3b2+5a2b
(2)6x3y-18xy2-3xy
(3)-x2y+4xy-5y2
(4)p(a2 + b2 )- q(a2 + b2 )
+
+
(1)
992+99.
(2)
5计算:
6.已知: 2x+y=4,xy=3,
求代数式2x2y+xy2的值
这节课你有哪些收获?
六、课堂小结
七 拓展作业
1.(必做题)课本P87习题第1、2题;
2. (选做题)思考:
(1)20042+2004能被2005整除吗?
(2)如果n是自然数,那么n2+n是奇数还是偶数?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
