苏科版七年级下册数学:10.4三元一次方程组 (共15张PPT)
文档属性
| 名称 | 苏科版七年级下册数学:10.4三元一次方程组 (共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 436.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览






文档简介
10.4 三元一次方程组
类比是获得发现的伟大源泉
足球比赛规则规定:胜一场得3分,平一场得
1分,负一场得0分。某足球队赛了22场得47分,且胜的场数比负的场数的4倍还多2,
该球队胜、平、负各多少场?
思考:题目中有几个未知量?
提出问题
你能用学过的方程(组)解决这个问题吗?
(2)如果设负了x场,则胜(4x+2)场,平(22-x-4x-2)场。
(1)如果设胜了x场,平了y场,则负了(22-x-y)场。
(3)如果设胜了x场,平了y场,负了z场。
你觉得设几个未知数列几个方程更直接呢?
3x+y=47
X=4( 22-x-y )+2
3(4x+2)+(20-5x)=47
x+y+z=22
3x+y=47
x=4z+2
解决问题
一元一次方程
二元一次方程组
x+y+z=22
3x+y=47
x=4z+2
现在能说说方程组有什么共同的特征吗?
操作观察
x+y+z=22
3x+y=47
x=4z+2
像这样,把含有三个未知数的三个一次方程联立在一起,就组成了一个三元一次方程组。
试一试:怎样解三元一次方程组呢?
形成概念
一元一次方程
二元一次方程组
三元一次方程组
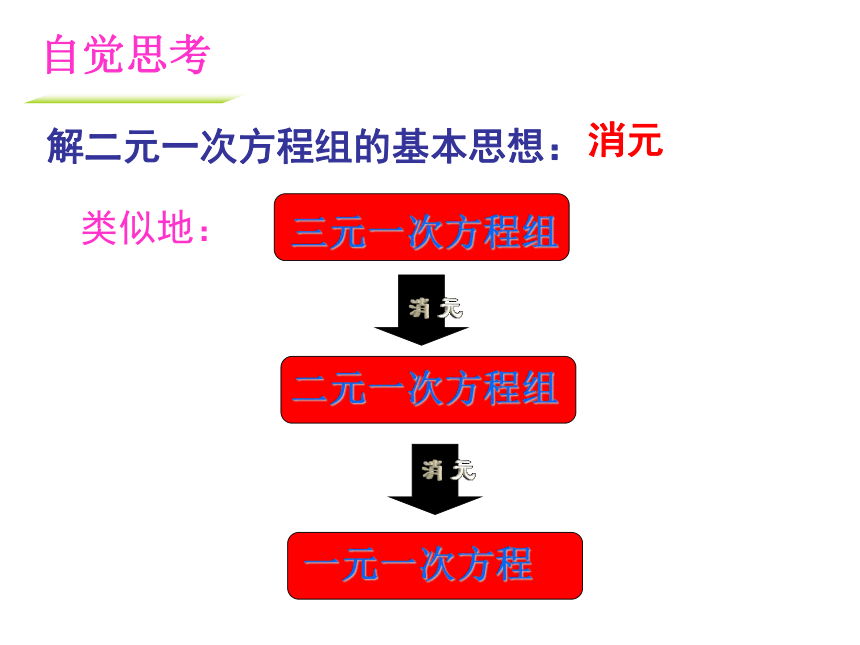
解二元一次方程组的基本思想:
类似地:
消元
自觉思考
①
②
③
解法1:将③代入①和②,得
解得
将z=3代入 得 x=14
所以原方程组的解是
5z+y=20
12z+y=41
y=5
z=3
③
x=14
y=5
z=3
例1 解方程组
采取怎样的方法来消元呢?
想一想:
还有其他方法吗?
代入消元法
例题讲解
解法2:①-②,得 -2x+z=-25 ④
③与④ 联立得
解得
将x=14代入② ,得 y=5
所以原方程组的解是
②
①
③
x=14
z=3
x=4z+2
-2x+z=-25
x=14
y=5
z=3
想一想:如何检验方程组的解是正确的?
用加减消元法
例2 解方程组
①
②
③
采取怎样的方法来消元呢?
3x +2y +5z=2
X -2y -z=6
4x +2y -7z=30
想一想:还有其他方法吗?
解三元一次方程组的关键是什么?
关键是消元。用代入或加减消元法消去
一个未知数,把解三元一次方程组转化为解
二元一次方程组。
小结
先想一想下列方程组中消去哪个未知数比较简便?再解方程组
小结:先观察方程组中未知数系数的特点,选择最佳的消元方法,使运算简便。
小试牛刀
①
②
③
①
②
③
解方程组
解:①+②+③,得2(x+y+z)=12
x+y+z=6 ④
④-①得 z=3
④-②得 x=2
④-③得 y=1
所以原方程组的解是
①
②
③
x=2
y=1
z=3
你能说出解方程组的思路吗?
整体思想
思维拓展
今有上等谷子三捆,中等谷子二捆,下等谷子一捆,共得谷子三十九斗;如果有上等谷子二捆,中等谷子三捆,下等谷子一捆,共得谷子三十四斗;上等谷子一捆,中等谷子二捆,下等谷子三捆,共得谷子二十六斗。问上、中、下三等的谷子每捆各可得几斗?
学以致用
三元一次方程组是刻画现实世界的有效模型。
实际
问题
列方程组
抽象思想
三元一次方程组
消元
转化
二元一次方程组
/一元一次方程
三元一次方程组的解
检验
实际问题的答案
解三元一
次方程组
①本节课,我学到了哪些知识?
②本节课,给我感受最深的是什么?
③课后你准备对哪方面进行进一步研究?
分享收获
你选择消去未知数_____,得到关于___的二元一次
方程组_______,解这个二元一次方程组,得_____,
原方程组的解是_____。
2. 解三元一次方程组
3.一个三位数,个位、百位上的数字的和等于十位上的数字,百位上的数字的7倍比个位、十位上的数字的和大2,个位、十位、百位上的数字的和是14.求这三位数。
①
②
③
1. 解三元一次方程组
课后作业
类比是获得发现的伟大源泉
足球比赛规则规定:胜一场得3分,平一场得
1分,负一场得0分。某足球队赛了22场得47分,且胜的场数比负的场数的4倍还多2,
该球队胜、平、负各多少场?
思考:题目中有几个未知量?
提出问题
你能用学过的方程(组)解决这个问题吗?
(2)如果设负了x场,则胜(4x+2)场,平(22-x-4x-2)场。
(1)如果设胜了x场,平了y场,则负了(22-x-y)场。
(3)如果设胜了x场,平了y场,负了z场。
你觉得设几个未知数列几个方程更直接呢?
3x+y=47
X=4( 22-x-y )+2
3(4x+2)+(20-5x)=47
x+y+z=22
3x+y=47
x=4z+2
解决问题
一元一次方程
二元一次方程组
x+y+z=22
3x+y=47
x=4z+2
现在能说说方程组有什么共同的特征吗?
操作观察
x+y+z=22
3x+y=47
x=4z+2
像这样,把含有三个未知数的三个一次方程联立在一起,就组成了一个三元一次方程组。
试一试:怎样解三元一次方程组呢?
形成概念
一元一次方程
二元一次方程组
三元一次方程组
解二元一次方程组的基本思想:
类似地:
消元
自觉思考
①
②
③
解法1:将③代入①和②,得
解得
将z=3代入 得 x=14
所以原方程组的解是
5z+y=20
12z+y=41
y=5
z=3
③
x=14
y=5
z=3
例1 解方程组
采取怎样的方法来消元呢?
想一想:
还有其他方法吗?
代入消元法
例题讲解
解法2:①-②,得 -2x+z=-25 ④
③与④ 联立得
解得
将x=14代入② ,得 y=5
所以原方程组的解是
②
①
③
x=14
z=3
x=4z+2
-2x+z=-25
x=14
y=5
z=3
想一想:如何检验方程组的解是正确的?
用加减消元法
例2 解方程组
①
②
③
采取怎样的方法来消元呢?
3x +2y +5z=2
X -2y -z=6
4x +2y -7z=30
想一想:还有其他方法吗?
解三元一次方程组的关键是什么?
关键是消元。用代入或加减消元法消去
一个未知数,把解三元一次方程组转化为解
二元一次方程组。
小结
先想一想下列方程组中消去哪个未知数比较简便?再解方程组
小结:先观察方程组中未知数系数的特点,选择最佳的消元方法,使运算简便。
小试牛刀
①
②
③
①
②
③
解方程组
解:①+②+③,得2(x+y+z)=12
x+y+z=6 ④
④-①得 z=3
④-②得 x=2
④-③得 y=1
所以原方程组的解是
①
②
③
x=2
y=1
z=3
你能说出解方程组的思路吗?
整体思想
思维拓展
今有上等谷子三捆,中等谷子二捆,下等谷子一捆,共得谷子三十九斗;如果有上等谷子二捆,中等谷子三捆,下等谷子一捆,共得谷子三十四斗;上等谷子一捆,中等谷子二捆,下等谷子三捆,共得谷子二十六斗。问上、中、下三等的谷子每捆各可得几斗?
学以致用
三元一次方程组是刻画现实世界的有效模型。
实际
问题
列方程组
抽象思想
三元一次方程组
消元
转化
二元一次方程组
/一元一次方程
三元一次方程组的解
检验
实际问题的答案
解三元一
次方程组
①本节课,我学到了哪些知识?
②本节课,给我感受最深的是什么?
③课后你准备对哪方面进行进一步研究?
分享收获
你选择消去未知数_____,得到关于___的二元一次
方程组_______,解这个二元一次方程组,得_____,
原方程组的解是_____。
2. 解三元一次方程组
3.一个三位数,个位、百位上的数字的和等于十位上的数字,百位上的数字的7倍比个位、十位上的数字的和大2,个位、十位、百位上的数字的和是14.求这三位数。
①
②
③
1. 解三元一次方程组
课后作业
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
